0. 前言

第一次看吴恩达老师机器学习视频时, 在 $9.2$ 节卡住。看到评论区别人解答(Arch725 的解答)发现有一些疏漏，而且缺少一些铺垫，所以进行了一些修改补充。

本文的反向传播算法的推导过程根据的是交叉熵代价函数，并非二次代价函数。不同代价函数的求导结果不同所以结果略有差异，但本质都是相同的。

交叉熵代价函数:

J(\Theta) = -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log(h_\theta(x^{(i)})) + (1-y^{(i)})log(1-h_\theta(x^{(i)})))

二次代价函数：

J(\Theta) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^{2}

本文参考自Arch725 的 github。如果读完后觉得有所收获, 请在里点个 star 吧～

1. 潜在读者

这篇文章的潜在读者为:

学习吴恩达机器学习课程, 看完 $9.1$ 节及以前的内容而在 $9.2$ 节一脸懵逼的同学
知道偏导数是什么, 也知道偏导数的求导法则这篇文章会帮助你完全搞懂 $9.2$ 节是怎么回事, 除 $9.1$ 节及以前的内容外, 不需要任何额外的机器学习的知识.

2. 铺垫

2.1 复合函数求导的链式法则

这里只提供公式方便大家回忆，若没有学习相关知识，请学习相关内容（偏导数）。

（链式法则）设 $u=f(x,y),x=\varphi(s,t),y=\phi(s,t)$ ，此时 $f$ 在点 $(x,y)$ 可微，又 $x$ 和 $y$ 都在点 $(s,t)$ 关于 $s,t$ 的偏导数存在，则

\frac{\partial{u}}{\partial{s}} = \frac{\partial{u}}{\partial{x}}*\frac{\partial{x}}{\partial{s}}+\frac{\partial{u}}{\partial{y}}*\frac{\partial{y}}{\partial{s}}

\frac{\partial{u}}{\partial{t}} = \frac{\partial{u}}{\partial{x}}*\frac{\partial{x}}{\partial{t}}+\frac{\partial{u}}{\partial{y}}*\frac{\partial{y}}{\partial{t}}

2.2 神经网络的各种记号

约定神经网络的层数为 $L$ , 其中第 $l$ 层的的神经元数为 $s_l$ , 该层第 $i$ 个神经元的输出值为 $a_i^{(l)}$ , 该层的每个神经元输出值计算如下:

a^{(l)} = \begin{bmatrix} a_1^{(l)} \\ a_2^{(l)} \\ \cdots \\ a_{s_l}^{(l)} \end{bmatrix} = sigmoid(z^{(l)}) = \frac{1}{1+e^{-z^{(l)}}} \tag{1}

其中 $sigmoid(z^{(l)})$ 是激活函数, $z^{(l)}$ 是上一层神经元输出结果 $a^{(l-1)}$ 的线性组合 $\Theta^{(l-1)}$ 是参数矩阵, $k^{(l-1)}$ 为常数向量:

z^{(l)} = {\Theta^{(l-1)}} a^{(l-1)} + k^{(l-1)} \tag{2}

\Theta^{(l-1)}_{(s_{l} \times s_{l-1})} = \begin{bmatrix} \theta_{11}^{(l-1)} & \theta_{12}^{(l-1)} & \cdots & \theta_{1s_{l-1}}^{(l-1)}\\ \theta_{21}^{(l-1)} & \theta_{22}^{(l-1)} & \cdots & \theta_{2s_{l-1}}^{(l-1)}\\ \vdots & \vdots & \ddots & \vdots \\ \theta_{s_{l}1}^{(l-1)} & \theta_{s_{l}2}^{(l-1)} & \cdots & \theta_{s_{l}s_{l-1}}^{(l-1)}\\ \end{bmatrix} \tag{3}

参数(权重)矩阵 $\Theta^{(l-1)}$ 的任务就是将第 $l-1$ 层的 $s_{l-1}$ 个参数线性组合为 $s_{l}$ 个参数, 其中 $\theta_{ij}^{l-1}$ 表示 $a_j^{(l-1)}$ 在 $a_i^{(l)}$ 中的权重(没错, 这里的 $i$ 是终点对序号, $j$ 是起点的序号), 用单一元素具体表示为:

z_i^{(l)} = \theta_{i1}^{(l-1)} * a_1^{(l-1)} + \theta_{i2}^{(l-1)} * a_2^{(l-1)} + \cdots + \theta_{is_{l-1}}^{(l-1)} * a_{s_{l-1}}^{(l-1)} + k_i^{(l-1)} = (\sum_{k=1}^{s_{l-1}} \theta_{ik}^{(l-1)} * a_k^{(l-1)}) + k_i^{(l-1)} \tag{4}

另外, 在 $logistic$ 回归中, 定义损失函数如下:

cost(a) = \begin{cases} \log(a) & y=1 \\ \log(1-a) & y=0 \end{cases} = y\log(a) + (1-y)\log(1-a) , y \in \{0, 1\} \tag{5}

记不住那么多符号可以看看下面的神经网络示例图。

3. 正式推导

据此, 我们的思路是, 计算出神经网络中的损失函数 $J(\Theta)$ , 然后通过梯度下降来求 $J(\Theta)$ 的极小值. 以一个 $3*4*4*3$ 的神经网络为例.图如下:

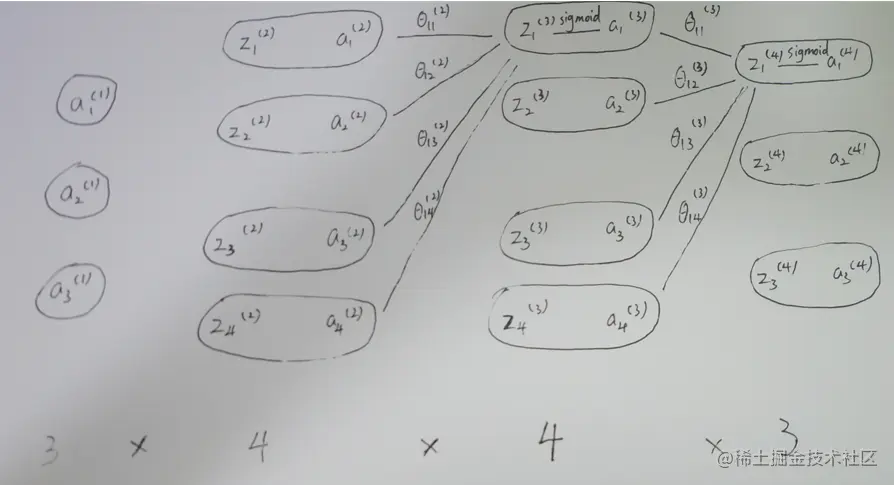
在该神经网络中, 损失函数如下:

J(\Theta) = y_1 \log(a_1^{(4)}) + (1-y_1) \log(1-a_1^{(4)}) \\ + y_2 \log(a_2^{(4)})+ (1-y_2) \log(1-a_2^{(4)}) \\ + y_3 \log(a_3^{(4)}) + (1-y_3) \log(1-a_3^{(4)}) \tag{6}

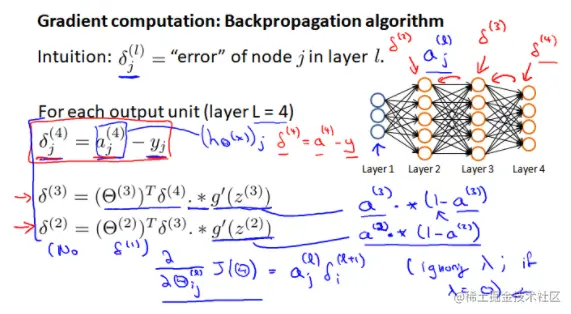
反向算法的精髓就是提出了一种算法, 让我们能快速地求出 $J(\Theta)$ 对 $\Theta$ 的各个分量的导数(这就是 $9.2$ 和 $9.3$ 节在做的工作). 相信大家在看到误差公式那里和我一样懵, 我们接下来就从根本目标——求偏导数入手, 先不管”误差”这个概念. 在求导的过程中, “误差”这一概念会更自然的浮现出来.

我们首先对于最后一层参数求导, 即 $\Theta^{(3)}$ . 首先明确, $\Theta^{(3)}$ 是一个 $3*4$ 的矩阵( $\Theta^{(3)} a^{(3)}_{(4 \times 1)} = z^{(4)}_{(3 \times 1)}$ ), $\frac{\partial{J}}{\partial{\Theta^{(3)}}}$ 也是一个 $3*4$ 矩阵, 我们需要对 $\Theta^{(3)}$ 的每一个分量求导. 让我们首先对 $\theta^{(3)}_{12}$ 求导:

\frac{\partial{J}}{\partial{\theta^{(3)}_{12}}} = \underbrace{\frac{\partial{J}}{\partial{a^{(4)}_{1}}}}_{(7.1)} * \underbrace{\frac{\partial{a^{(4)}_{1}}}{\partial{z^{(4)}_{1}}}}_{(7.2)} * \underbrace{\frac{\partial{z^{(4)}_{1}}}{\partial{\theta_{12}^{(3)}}}}_{(7.3)} \tag{7}

分别由式 $(6)$ , $(1)$ , $(4)$ 知:

(7.1) = \frac{\partial{J}}{\partial{a^{(4)}_{1}}} = \frac{y_1}{a_1^{(4)}} - \frac{1-y_1}{1-a_1^{(4)}} \tag{8}

(7.2) = \frac{\partial{a^{(4)}_{1}}}{\partial{z^{(4)}_{1}}} = \frac{-e^{-z_1^{(4)}}}{{(1 + e^{-z_1^{(4)}})}^2} = \frac{1}{1 + e^{-z_1^{(4)}}} * (1 - \frac{1}{1 + e^{-z_1^{(4)}}}) = a^{(4)}_{1} (1-a^{(4)}_{1}) \tag{9}

(7.3) = \frac{\partial{z^{(4)}_{1}}}{\partial{\theta_{12}^{(3)}}} = a_{2}^{(3)} \tag{10}

代入 $(7)$ 知:

\frac{\partial{J}}{\partial{\theta^{(3)}_{12}}} = (y_1(1-a_1^{(4)})-(1-y_1)a_1^{(4)})a_2^{(3)} = (y_1-a_1^{(4)})a_2^{(3)} \tag{11}

同理可知 $J(\Theta)$ 对 $\Theta^{(3)}$ 其他分量的导数. 将 $\frac{\partial{J}}{\partial{\Theta^{(3)}}}$ 写成矩阵形式:

\frac{\partial{J}}{\partial{\Theta^{(3)}}} = \begin{bmatrix} (y_1-a_1^{(4)})a_1^{(3)} & (y_1-a_1^{(4)})a_2^{(3)} & (y_1-a_1^{(4)})a_3^{(3)} & (y_1-a_1^{(4)})a_4^{(3)} \\ (y_2-a_2^{(4)})a_1^{(3)} & (y_2-a_2^{(4)})a_2^{(3)} & (y_2-a_2^{(4)})a_3^{(3)} & (y_1-a_1^{(4)})a_4^{(3)} \\ (y_3-a_3^{(4)})a_1^{(3)} & (y_3-a_3^{(4)})a_2^{(3)} & (y_3-a_3^{(4)})a_3^{(3)} & (y_1-a_1^{(4)})a_4^{(3)} \\ \end{bmatrix} \tag{12}

如果我们定义一个“误差”向量为 $\delta^{(4)} = \begin{bmatrix}(y_1-a_1^{(4)}) & (y_2-a_2^{(4)}) & (y_3-a_3^{(4)})\end{bmatrix}^T$ , 衡量最后一层神经元的输出与真实值之间的差异, 那么 $(12)$ 可以写成两个矩阵相乘的形式:

\frac{\partial{J}}{\partial{\Theta^{(3)}}} = \delta^{(4)} \begin{bmatrix} a_1^{(3)} & a_2^{(3)} & a_3^{(3)} & a_4^{(3)} \end{bmatrix} = \delta^{(4)}_{(3 \times 1)} (a^{(3)})^T_{(1 \times 4)} \tag{13}

让我们先记下这个式子, 做接下来的工作: 计算 $\frac{\partial{J}}{\partial{\Theta^{(2)}}}$ . 和计算 $\frac{\partial{J}}{\partial{\Theta^{(3)}}}$ 一样, 让我们先计算 $\frac{\partial{J}}{\theta^{(2)}_{12}}$ :

\frac{\partial{J}}{\partial{\theta^{(2)}_{12}}} = \underbrace{\frac{\partial{J}}{\partial{a^{(3)}_{1}}}}_{(14.1)} * \underbrace{\frac{\partial{a^{(3)}_{1}}}{\partial{z^{(3)}_{1}}}}_{(14.2)} * \underbrace{\frac{\partial{z^{(3)}_{1}}}{\partial{\theta_{12}^{(2)}}}}_{(14.3)} \tag{14}

${\theta^{(2)}_{12}}$ 对 $J(\Theta)$ 求导，根据偏导数的求导法则，要找到 $J(\Theta)$ 中所有与 ${\theta^{(2)}_{12}}$ 有关的项进行链式求导。由上式可以看出 ${\theta^{(2)}_{12}}$ 只是 $a_1^{(3)}$ 的变量，所以只需要考虑 $J(\Theta)$ 有多少项和 $a_1^{(3)}$ 相关。

z_1^{(4)} = \theta_{11}^{(3)}*a_1^{(3)} + \theta_{12}^{(3)}*a_2^{(3)} + \theta_{13}^{(3)}*a_3^{(3)} +\theta_{14}^{(3)}*a_4^{(3)} + k_1^{(4)}

z_2^{(4)} = \theta_{21}^{(3)}*a_1^{(3)} + \theta_{22}^{(3)}*a_2^{(3)} + \theta_{23}^{(3)}*a_3^{(3)} +\theta_{24}^{(3)}*a_4^{(3)}+ k_2^{(4)}

z_3^{(4)} = \theta_{31}^{(3)}*a_1^{(3)} + \theta_{32}^{(3)}*a_2^{(3)} + \theta_{33}^{(3)}*a_3^{(3)} +\theta_{34}^{(3)}*a_4^{(3)}+ k_3^{(4)}

上面三式是最后一层 $z^{(4)}$ 的求和过程，可以看到 $z_1^{(4)},z_2^{(4)},z_3^{(4)}$ 中都包含 $a_1^{(3)}$ ，所以 $(14.1)$ 式还可以做如下拆分:

(14.1) = \frac{\partial{J}}{\partial{a_1^{(3)}}} = \underbrace{\frac{\partial{J}}{\partial{a^{(4)}_{1}}} * \frac{\partial{a^{(4)}_{1}}}{\partial{z^{(4)}_{1}}} * \frac{\partial{z^{(4)}_{1}}}{\partial{a^{(3)}_{1}}}}_{(15.1)} + \underbrace{\frac{\partial{J}}{\partial{a^{(4)}_{2}}} * \frac{\partial{a^{(4)}_{2}}}{\partial{z^{(4)}_{2}}} * \frac{\partial{z^{(4)}_{2}}}{\partial{a^{(3)}_{1}}}}_{(15.2)} + \underbrace{\frac{\partial{J}}{\partial{a^{(4)}_{3}}} * \frac{\partial{a^{(4)}_{3}}}{\partial{z^{(4)}_{3}}} * \frac{\partial{z^{(4)}_{3}}}{\partial{a^{(3)}_{1}}}}_{(15.3)} \tag{15}

注意到 $(15.1)$ , $(15.2)$ 与 $(15.3)$ 式都和 $(7)$ 式类似, 三式子可分别化为:

(15.1) = \frac{\partial{J}}{\partial{a^{(4)}_{1}}} * \frac{\partial{a^{(4)}_{1}}}{\partial{z^{(4)}_{1}}} * \frac{\partial{z^{(4)}_{1}}}{\partial{a^{(3)}_{1}}} = (y_1-a_1^{(4)})\theta_{11}^{(3)} \tag{16}

(15.2) = \frac{\partial{J}}{\partial{a^{(4)}_{2}}} * \frac{\partial{a^{(4)}_{2}}}{\partial{z^{(4)}_{2}}} * \frac{\partial{z^{(4)}_{2}}}{\partial{a^{(3)}_{1}}} = (y_2-a_2^{(4)})\theta_{21}^{(3)} \tag{17}

(15.3) = \frac{\partial{J}}{\partial{a^{(4)}_{3}}} * \frac{\partial{a^{(4)}_{3}}}{\partial{z^{(4)}_{3}}} * \frac{\partial{z^{(4)}_{3}}}{\partial{a^{(3)}_{1}}} = (y_3-a_3^{(4)})\theta_{31}^{(3)} \tag{18}

将 $(16)$ , $(17)$ , $(18)$ 代入 $(19)$ :

(14.1) = \frac{\partial{J}}{\partial{\theta^{(2)}_{12}}} = (y_1-a_1^{(4)})\theta_{11}^{(3)} + (y_2-a_2^{(4)})\theta_{21}^{(3)} + (y_3-a_3^{(4)})\theta_{31}^{(3)} \tag{19}

另外, 与 $(9)$ , $(10)$ 类似, 可以得到 $(14.2)$ 和 $(14.3)$ :

(14.2) = \frac{\partial{a^{(3)}_{1}}}{\partial{z^{(3)}_{1}}} = a^{(3)}_{1} (1-a^{(3)}_{1}) \tag{20}

(14.3) = \frac{\partial{z^{(3)}_{1}}}{\partial{\theta^{(2)}_{12}}} = a_{2}^{(2)} \tag{21}

将 $(19)$ , $(20)$ , $(21)$ 共同代入 $(14)$ , 得到 $\frac{\partial{J}}{\theta^{(2)}_{12}}$ :

\frac{\partial{J}}{\partial{\theta^{(2)}_{12}}} = [(y_1-a_1^{(4)})\theta_{11}^{(3)} + (y_2-a_2^{(4)})\theta_{21}^{(3)} + (y_3-a_3^{(4)})\theta_{31}^{(3)}] a^{(3)}_{1} (1-a^{(3)}_{1}) a_{2}^{(2)} \tag{22}

同理也可知 $J(\Theta)$ 对 $\Theta^{(2)}$ 其他分量的导数. 将 $\frac{\partial{J}}{\partial{\Theta^{(2)}}}$ 写成矩阵形式:

$(23)$ 只是看起来很复杂, 实际上只是一个普通的 $(4*4)$ 矩阵. 让我们先参考 $(13)$ 将 ${a^{(2)}}^T$ 拆出来:

\frac{\partial{J}}{\partial{\Theta^{(2)}}}_{4 \times 4} = \underbrace{\begin{bmatrix} \{[(y_1-a_1^{(4)})\theta_{11}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{21}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{31}^{(3)}] \\ *a^{(3)}_{1}(1-a^{(3)}_{1})\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{12}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{22}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{32}^{(3)}] \\ *a^{(3)}_{2} (1-a^{(3)}_{2})\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{13}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{23}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{33}^{(3)}] \\ *a^{(3)}_{3} (1-a^{(3)}_{3})\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{14}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{24}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{34}^{(3)}] \\ *a^{(3)}_{4} (1-a^{(3)}_{4})\} \end{bmatrix}_{4 \times 1}}_{24.1} \circ \underbrace{\begin{bmatrix} a_{1}^{(2)} & a_{2}^{(2)} & a_{3}^{(2)} & a_{4}^{(2)} \end{bmatrix}_{1 \times 4}}_{24.2} \tag{24}

其中 $(24.2)$ 是我们熟悉的 ${a^{(2)}}^T$ , 而我们先暂时定义 $(24.1)$ 为 $\delta^{(3)}$ (先不管它的实际意义), 引入 $Hadamard$ 积的概念(就是 $9.2$ 节视频中的 $·*$ 符号), 对 $\delta^{(3)}$ 进一步拆分:

\delta^{(3)} = \begin{bmatrix} \{[(y_1-a_1^{(4)})\theta_{11}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{21}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{31}^{(3)}]\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{12}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{22}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{32}^{(3)}]\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{13}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{23}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{33}^{(3)}]\} \\ \\ \{[(y_1-a_1^{(4)})\theta_{14}^{(3)} \\ + (y_2-a_2^{(4)})\theta_{24}^{(3)} \\ + (y_3-a_3^{(4)})\theta_{34}^{(3)}]\} \end{bmatrix} \circ \begin{bmatrix} a^{(3)}_{1} (1-a^{(3)}_{1}) \\ a^{(3)}_{2} (1-a^{(3)}_{2}) \\ a^{(3)}_{3} (1-a^{(3)}_{3}) \\ a^{(3)}_{4} (1-a^{(3)}_{4}) \end{bmatrix} = \\ \begin{bmatrix} \theta_{11}^{(3)} & \theta_{21}^{(3)} & \theta_{31}^{(3)} \\ \theta_{12}^{(3)} & \theta_{22}^{(3)} & \theta_{32}^{(3)} \\ \theta_{13}^{(3)} & \theta_{23}^{(3)} & \theta_{33}^{(3)} \\ \theta_{14}^{(3)} & \theta_{24}^{(3)} & \theta_{34}^{(3)} \\ \end{bmatrix} \circ \begin{bmatrix} y_1-a_1^{(4)} \\ y_2-a_2^{(4)} \\ y_3-a_3^{(4)} \end{bmatrix} \tag{25} \circ \begin{bmatrix} a^{(3)}_{1} (1-a^{(3)}_{1}) \\ a^{(3)}_{2} (1-a^{(3)}_{2}) \\ a^{(3)}_{3} (1-a^{(3)}_{3}) \\ a^{(3)}_{4} (1-a^{(3)}_{4}) \end{bmatrix} = {\Theta^{(3)}}^T \delta^{(4)} \circ \frac{\partial{a^{(3)}}}{\partial{z^{(3)}}}

综合 $(24)$ , $(25)$ 式可以得到:

\frac{\partial{J}}{\partial{\Theta^{(2)}}} = \delta^{(3)} {a^{(2)}}^T \tag{26}

其中

\delta^{(3)} = {\Theta^{(3)}}^T \delta^{(4)} \circ \frac{\partial{a^{(3)}}}{\partial{z^{(3)}}} \tag{27}

至此, 基本大功告成. 让我们将 $(26)$ , $(27)$ 与 $(13)$ 对照观察:

\frac{\partial{J}}{\partial{\Theta^{(3)}}} = \delta^{(4)} {a^{(3)}}^T

\frac{\partial{J}}{\partial{\Theta^{(2)}}} = \delta^{(3)} {a^{(2)}}^T

\delta^{(3)} = {\Theta^{(3)}}^T \delta^{(4)} \circ \frac{\partial{a^{(3)}}}{\partial{z^{(3)}}} \tag{28}

归纳总结即可推广到 $L$ 层的神经网络:

\frac{\partial{J}}{\partial{\Theta^{(l)}}} = \delta^{(l+1)} {a^{(l)}}^T

\delta^{(l)} = \begin{cases} 0 & l=0 \\ {\Theta^{(l)}}^T \delta^{(l+1)} \circ \frac{\partial{a^{(l)}}}{\partial{z^{(l)}}} & 1\leqslant{l}\leqslant{L-1} \\ y-a^{(l)} & l=L \end{cases} \tag{29}

其中 $\frac{\partial{a^{(l)}}}{\partial{z^{(l)}}}$ 就是 $sigmoid(x)$ 求导. 根据 $(29)$ , 我们就可以顺利、轻松、较快速地迭代求出 $J(\Theta)$ 对 $\Theta$ 的各个分量的导数.

对比吴恩达课程中的结果可以发现是完全相同的。

反向传播算法推导(交叉熵代价函数-吴恩达机器学习)