2 PAC学习框架 （page 18 19）

示例2.2布尔文字的连接

考虑学习最多$n$个布尔文字$x_1，…，x_n$的连接的概念类$C_n$.布尔文字是变量$x_i$，$i∈ [1，n]$，或其否定$\overline x_i$。对于$n=4$，一个例子是合取:$x_1∧ \overline x_2∧ x_4$，其中$\overline x_2$表示布尔文字$x_2$的否定。$(1,0,0,1)$是这个概念的正面例子，而$(1,0,0,0)$是负面例子。

请注意，对于 $n = 4$，正例 $(1,0,1,0)$ 意味着目标概念不能包含文字 $\overline x_1$ 和 $\overline x_3$，也不能包含文字 $x2$ 和 $x4$。相比之下，一个反面例子没有那么丰富，因为它不知道它的 $n$ 位中的哪一个是不正确的。因此，一个用于寻找一致假设的简单算法基于正例，包括以下内容：对于每个正例 $(b_1,...,b_n)$ 和 $i ∈ [1,n]$，如果 $b_i = 1$ 则 $\overline x_i$ 被排除作为概念类中可能的文字，如果 $b_i = 0$，则排除 $x_i$。因此，未排除的所有文字的合取是与目标一致的假设。图 2.4 显示了示例训练样本以及 $n = 6$情况下的一致假设。

我们有 $|H| = |Cn| = 3^n$，因为每个文字都可以肯定包含，否定包含或不包含。将其插入到一致假设的样本复杂度界限中，对于任何 $\epsilon > 0$ 和 $δ > 0$ 产生以下样本复杂度界限:

因此，最多 $n$ 个布尔文字的连接类是 PAC 可学习的。请注意，计算复杂度也是多项式的，因为每个示例的训练成本为 $O(n)$。对于 $δ = 0.02$、$\epsilon = 0.1$ 和 $n = 10$，界限变为 $m ≥ 149$。因此，对于至少有 $149$ 个样本的标记样本，界限保证 $99\%$ 的准确度和至少 $98\%$ 的置信度。

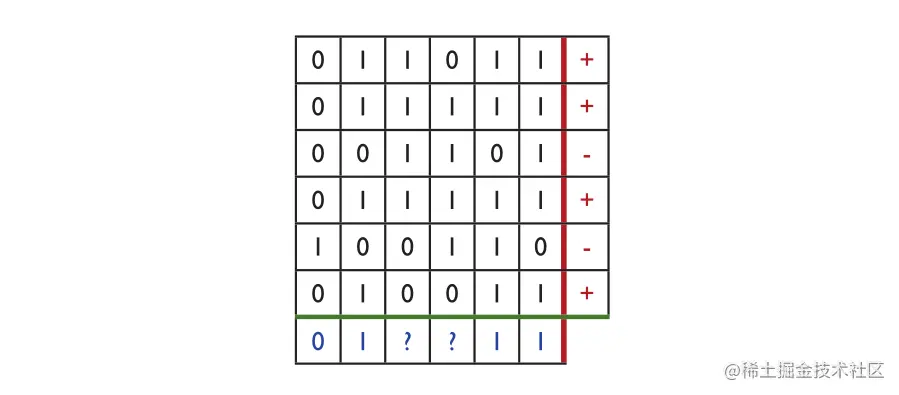
图片2.4 表格的前六行中的每一行都代表一个训练示例，其标签 $+$ 或 $-$ 在最后一列中指示。如果所有正例的第 $i$ 个条目为 $0$（或者 $1$），则最后一行在列 $i ∈ [1, 6]$ 中包含 $0$（或者 $1$）。如果 $0$ 和 $1$ 都作为某个正面示例的第 $i$ 个条目出现，那么它包含 '' $？$''。因此，对于这个训练样本，文中描述的一致性算法返回的假设是 $\overline x_1 ∧x_2 ∧x_5 ∧x_6$。

示例 2.3 通用概念类

考虑具有 $n$ 个分量的所有布尔向量的集合 $X = \{0, 1\}^n$，并让 $U_n$ 是由 $X$ 的所有子集形成的概念类。这个概念课是 PAC 可学习的吗？为了保证一致的假设，假设类必须包括概念类，因此 $|H| ≥ |U_n| = 2^{(2^n)}$。定理 2.1 给出了以下样本复杂度界限：

这里，所需的训练样本数量是 $n$ 的指数，这是 $X$ 中点的表示的成本。因此，PAC 学习不能由定理保证。事实上，不难证明这个通用概念类不是 PAC 可学习的。