这是我参与8月更文挑战的第8天，活动详情查看：8月更文挑战

本文为吴恩达机器学习课程的笔记系列第二篇，主要学习神经网络前向传播与反向传播的算法原理及推导。

神经网络基础

概念介绍

人工神经网络（Artificial Neural Network）简称神经网络（NN）。神经网络是一种模拟人体神经元结构的数学模型，其神经元的连接是固定的。靠正向和反向传播来更新神经元。简单来说，神经网络是由一连串的神经层组成，每一层神经层里面存在有很多的神经元。

神经网络从逻辑上可以分为三层：

• 输入层（Input Layer）：第一层，接收特征 $x$。
• 输出层（Output Layer）：最后一层，输出最终预测的假设 $h$。
• 隐藏层（HiddenLayers）：中间层，并不直接可见。

特点：

• 每一种神经网络都会有输入输出值
• 如何被训练：
  • 大量的数据集
  • 成千上万次的训练
  • 错误中学习经验，对比预测答案与真实答案差别，反向传播改进识别。

下面以最简单的二层神经网络为例来具体介绍：

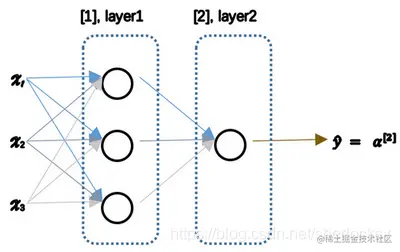
在上图神经网络中，记输入特征向量为 $x$ ，权重参数矩阵 $W$ ，偏置参数 $b$，$a$ 表示每个神经元的输出，上标表示神经网络的层数（隐藏层为1）。

公式：

• $z=W^Tx+b$
• $a=g(z)=\dfrac{1}{1+e^{-z}}$

神经网络的计算步骤：

• 首先计算第一层网络中各节点相关数 $z^{[1]}=W^{[1]^T} x+b$
• 使用激活函数计算 $a^{[1]} = g(z^{[1]})$
• 下一层同理，如此计算，直至输出最后的 $a^{[2]}$
• 可得最终的损失函数 $Loss(a^{[2]},y)$

向量化计算

第一层公式：

$\begin{bmatrix}z_1^{[1]} \\z_2^{[1]} \\z_3^{[1]} \end{bmatrix}_{3\times1}=\begin{bmatrix}W_{11}^{[1]^T}...\\W_{21}^{[1]^T}...\\W_{31}^{[1]^T}...\\\end{bmatrix}_{3\times3}*\begin{bmatrix}x_1\\x_2\\x_3\\ \end{bmatrix}_{3\times1}+\begin{bmatrix}b_1^{[1]}\\b_2^{[1]}\\b_3^{[1]}\\\end{bmatrix}_{3\times1}$

$\begin{bmatrix}a_1^{[1]} \\a_2^{[1]} \\a_3^{[1]} \end{bmatrix}_{3\times1}=\begin{bmatrix}g(z_1^{[1]})\\g(z_2^{[1]}) \\g(z_3^{[1]}) \end{bmatrix}_{3\times1}$

第二层公式:

$\begin{bmatrix}z^{[2]}\end{bmatrix}_{1\times1}=\begin{bmatrix}W_{11}^{[2]^T}...\end{bmatrix}_{1\times3}*\begin{bmatrix}a_1^{[1]} \\a_2^{[1]} \\a_3^{[1]} \end{bmatrix}_{3\times1}+\begin{bmatrix}b^{[2]}\end{bmatrix}_{1\times1}$

$\begin{bmatrix}a^{[2]}\end{bmatrix}_{1\times1}=\begin{bmatrix}g(z^{[2]})\end{bmatrix}_{1\times1}$

输出层：

$Loss(a^{[2]},y)=-ylog(a^{[2]})-(1-y)log(1-a^{[2]})$

这个公式与逻辑回归中的代价函数十分相似。

前向传播

通俗的理解，从输入层开始，每一层计算出 $a^{[i]}(z)$ 值，一层一层往下不停计算直至输出层输出最终值，然后与标签值求得误差 $Loss$ 的过程称为前向传播（Forward propagation ）。

上述例子的前向传播过程即：

1. $z^{[1]}=W^{[1]}x+b^{[1]}$
2. $a^{[1]}=g(z^{[1]})$
3. $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
4. $a^{[2]}=g(z^{[2]})$
5. $Loss(a^{[2]},y)=-ylog(a^{[2]})-(1-y)log(1-a^{[2]})$

多样本向量化

所谓多样本，就是当输入特征不再是一个简单的向量，而是一个矩阵。原理实际上是相同的，唯一需要注意的地方就是矩阵维度要匹配。

假设训练样本为$m$个，相应的，上述的公式需要更新如下：

• $Z=W^TX+b$
• 对单个样本： $z^{[1](i)}=W^Tx^{(i)}+b^{[1]}$
• $X=\begin{bmatrix} \vdots&\vdots&\vdots\\x^{(1)}&x^{(2)}&x^{(m)}\\\vdots&\vdots&\vdots\end{bmatrix}$
• $Z^{[1]}=\begin{bmatrix} \vdots&\vdots&\vdots\\z^{[1](1)}&z^{[1](2)}&z^{[1](m)}\\\vdots&\vdots&\vdots\end{bmatrix}$
• $A^{[1]}=\begin{bmatrix} \vdots&\vdots&\vdots\\a^{[1](1)}&a^{[1](2)}&a^{[1](m)}\\\vdots&\vdots&\vdots\end{bmatrix}$

激活函数

为什么需要非线性激活函数？

若去掉激活函数或激活函数为线性，则任何两个线性函数的组合还是线性的，这样会导致不管神经网络多少层，你所做的运算一直是计算线性函数，隐藏层就失去作用。

下面是三种常见的激活函数：

$\mathbf {Sigmoid}$ 函数

• $\sigma(z)=\dfrac{1}{1+e^{-z}}$
• $\sigma'(z)=\sigma(z)(1-\sigma(z))$ 非常好用的性质
• 

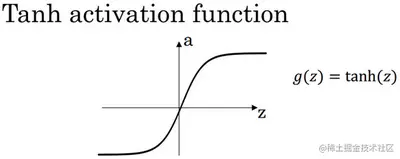
$\mathbf {tanh}$ 函数

• $tanh(z)=\dfrac{e^z-e^{-z}}{e^z+e^{-z}}$
• 显然值域为 $[-1,1]$
• $tanh'(z)=1-(tanh(z))^2$
• 

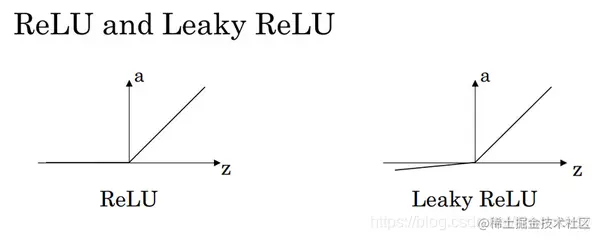
$\mathbf {Relu}$ 函数

• $g(z)=max(0,z)$

• $g'(z)=\begin{cases}0&if\;z<0 \\1&if\;z>0\\undefined&if\;z=0\end{cases}$

• $Leaky Relu$ 函数

  • $g(z)=max(0.01z,z)$
  • $g'(z)=\begin{cases}0.01&if\;z<0 \\1&if\;z>0\\undefined&if\;z=0\end{cases}$

• 

• 使用最为广泛

神经网络梯度下降机制

我们知道，神经网络可以含有多个隐含层，每一层的神经元都会产出预测，而最终的误差是在输出层计算的，那如何优化最后的损失函数 $L(a^{[i]},y)$ ？

传统回归问题如逻辑回归的梯度下降法则显然在此不能直接适用，因为我们需要逐层考虑误差，并且逐层优化，为此，神经网络中采用反向传播算法（Back Propagation Algorithm）来优化误差。

反向传播推导

首先，回顾一下损失函数 loss function：

• $Loss(a^{[L]},y)=-ylog(a^{[L]})-(1-y)log(1-a^{[L]})$

我们知道前向传播是从输入层一步一步从前往后计算出最终值，那反向传播，顾名思义，其实就是从后往前推导，只不过这个推导的过程就是基于最后的损失函数，不停往前求偏导。求导的方法就是基于链式法则。

从前面我们知道前向传播过程：

1. $z^{[1]}=W^{[1]}x+b^{[1]}$
2. $a^{[1]}=g(z^{[1]})$
3. $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
4. $a^{[2]}=g(z^{[2]})$
5. $Loss(a^{[2]},y)=-ylog(a^{[2]})-(1-y)log(1-a^{[2]})$

则反向传播过程如下：

输出层：

1. $da^{[2]}=\dfrac{\partial Loss}{\partial a^{[2]}}=-\dfrac{y}{a^{[2]}}+\dfrac{1-y}{1-a^{[2]}}$
2. $dz^{[2]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}=(-\dfrac{y}{a^{[2]}}+\dfrac{1-y}{1-a^{[2]}})\cdot a^{[2]}(1-a^{[2]})=a^{[2]}-y$
3. $dW^{[2]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d W^{[2]}}=dz^{[2]}a^{[1]^T}$
4. $db^{[2]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d b^{[2]}}=dz^{[2]}$

第二层：

1. $da^{[1]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d a^{[1]}}=W^{[2]^T}dz^{[2]}$
2. $dz^{[1]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d a^{[1]}}\cdot\dfrac{d a^{[1]}}{d z^{[1]}}=W^{[2]^T}dz^{[2]}*g'(z^{[1]})$
3. $dW^{[1]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d a^{[1]}}\cdot\dfrac{d a^{[1]}}{d z^{[1]}}\cdot\dfrac{d z^{[1]}}{d W^{[1]}}=dz^{[1]}x^T$
4. $db^{[1]}=\dfrac{\partial Loss}{\partial a^{[2]}}\cdot\dfrac{d a^{[2]}}{d z^{[2]}}\cdot\dfrac{d z^{[2]}}{d a^{[1]}}\cdot\dfrac{d a^{[1]}}{d z^{[1]}}\cdot\dfrac{d z^{[1]}}{d b^{[1]}}=dz^{[1]}$

输入层不用计算。

我们定义各层的误差为向量 $\delta^{(l)}$，$l$ 表示第几层，$L$ 表示总共层数。从上述推导中我们可以得到：

$\delta^{(l)}=\begin{cases}a^{(l)}-y&l=L\\W^{[l+1]^T}dz^{[l+1]}*g^{[l]\prime}(z^{[l]}) &l=2,3,...,L-1 \end{cases}$

对于m个样本，则

1. $dz^{[2]}=A^{[2]}-y$
2. $dW^{[2]}=\dfrac{1}{m}dz^{[2]}a^{[1]^T}$
3. $db^{[2]}=\dfrac{1}{m} np.sum(dZ^{[2]},axis=1,keepdims=True)$

以上就是对反向传播的详细推导，如果能理解链式求导，那反向传播的原理推导将会非常容易理解。