[译] JavaScript 实现图数据结构

CarlosChen
247 阅读10分钟

JavaScript 实现图数据结构

图数据结构帮助我们创建许多强大的东西，你使用它实现非线性数据结构的可能性很高。它常用于许多数据节点之间的多重复杂连接，这也使他特别适合展示地图、网络和导航系统。

这篇文章的视频讲解

这篇文章是 Youtube 上图数据结构系列的详细的改进文章版，如果你喜欢视频，你可以点击上面的 URL 观看原始视频。。

观看视频

什么是图？

图是一种非线性的抽象数据结构，这意味着它由行为定义，而不是由强调数据模型定义。

它由一组节点组成 —— 也被称为由边（线）连接的顶点。如果这些顶点由方向，这个图就被称为有向图，如果两个节点的边间相互指向，那么我们就称这两个节点强连通。

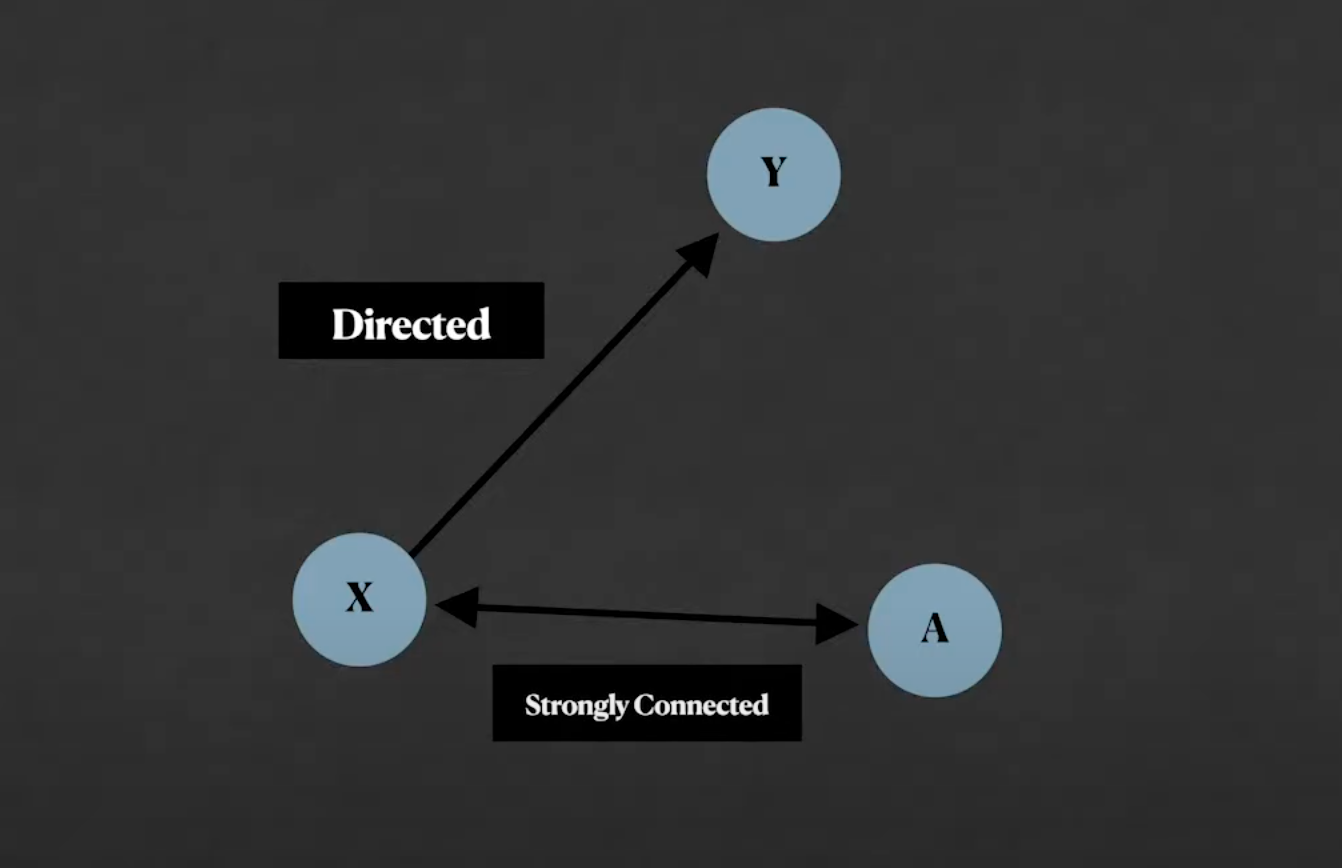
边也可以有权重，这意味着边也有值，当你表示一个地图时，这类信息非常有用。例如，如果我们把边当作路，把位置当作节点，我们可以给出这些边的距离值，我们就可以通过添加节点之间的边的值，来知道一个节点离另一个节点有多远。

什么时候使用图数据结构？

在一个列表数据结构中，你有一个按顺序排列的元素集合，它需要你一个一个遍历，直到你找到你想要的那个元素。在像树一样的分层数据结构中，你有父子关系，可以让你去决定要导航到哪棵子树。在图数据结构中，你有邻接点。

在图中一个元素（或者说一个节点）只知道它连接的节点，这些节点连接更多节点，以此类推。这种复杂关系类型，是数据需要用图表示的主要特征。

例如 GPS 系统和地图等可以用图表示，它将许多节点连接在一起，这样就可以帮助确定如何从一个点到达另一个点，以及他们之间有多长或多远。

社交网络以人作为节点，可以用图表来表示，例如，通过校验这些人与谁有联系，来帮助找出两个人有多少共同的朋友或兴趣爱好

互联网是一个大图，搜索引擎通过图表这种方式，来决定网站之间的连接。

当非线性或分层之间存在复杂的联系时，就需要一个图。更清晰的说，一个线性数据结构有起始节点和结束节点，分层结构有一个起始节点，以及许多结束节点，这取决于你遵循的路径。图有多个起始节点和结束节点，如果你的数据遵循这个模式，你可能需要用到图。

简单实现图

图用于表示复杂的数据关系，但是图的实现本身非常简单。

你可能需要理解的一件事是矩阵和邻接表的概念。例如，下面这个简单的图可以用邻接矩阵或邻接列表，甚至用关联矩阵表示，这取决于你想表示什么类型，以及你想要用它做什么。

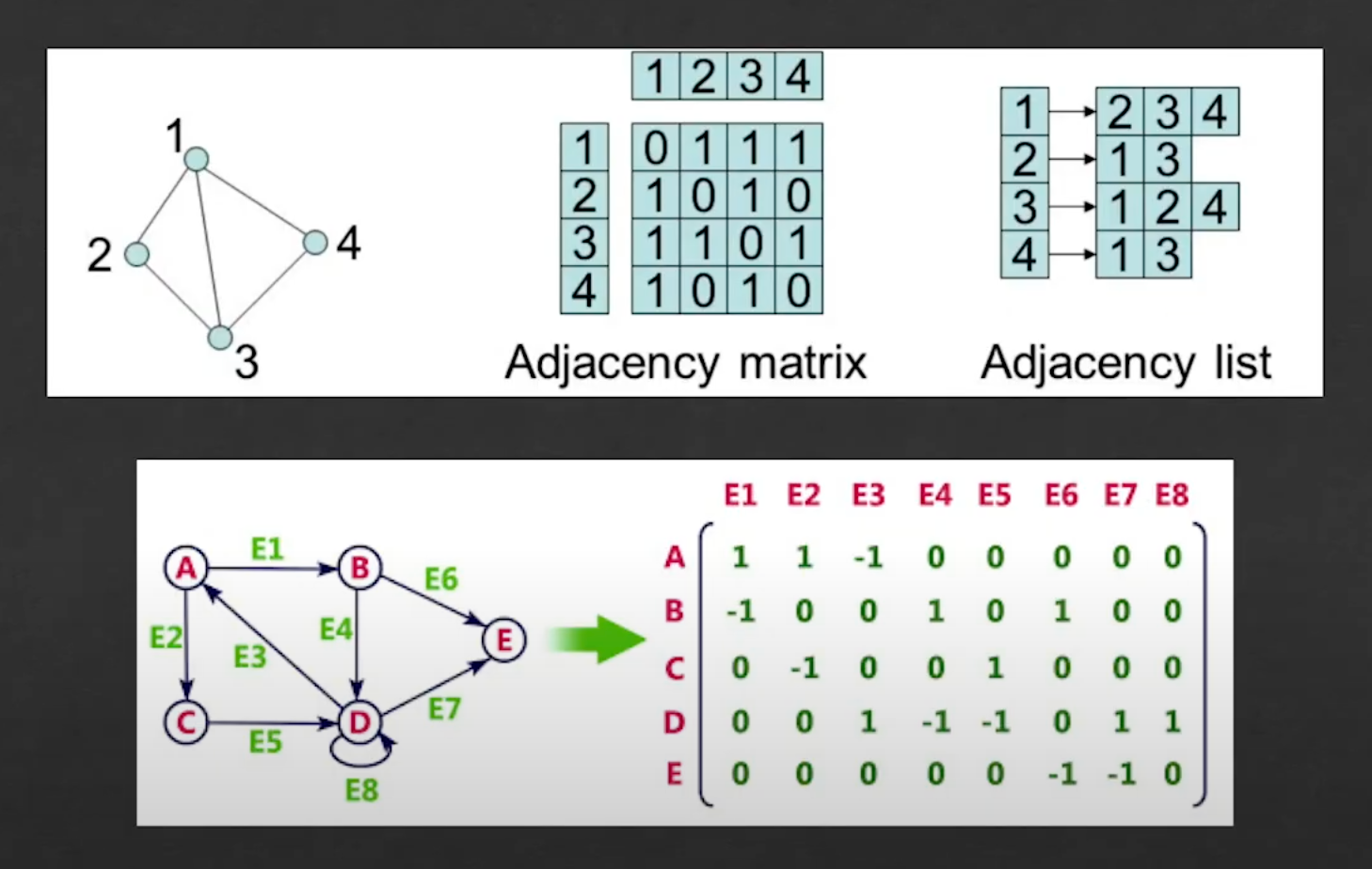
  • 邻接矩阵就像一个表，用 1 表示节点连接，用 0 表示节点不连接。这种方法很适合表示有限图。
  • 邻接表类似于字典其中每个节点值都是它连接到的所有节点的列表。这是用来表示有限图的另一种方法，它更快，更容易处理。
  • 关联矩阵也类似一个表，但不同的是，它追踪两个节点是否连接，它追踪边的方向，1 表示它用边去连接其他的节点，-1 表示别的节点用边连接它，0 表示没有连接到这个节点的边。当你拥有带有方向和值(权重)的边时，这种方法非常适合，用于表示地图和导航系统。

对于这个图的实现，我将会用邻接列表去简化，我给你们看的图是通用的，未加权重的。

我们将先声明一个带私有顶点列表的图类，该列表使用 set 数据结构来确保它不会包含重复的边，并且，一个私有邻接列表用 map 数据结构来跟踪节点的连接。

class Graph {
  #vertices = new Set();
  #adjacentList = new Map();
  
  get vertices() {
    return Array.from(this.#vertices)
  }
  
  get adjacentList() {
    const list = {};
    
    this.#adjacentList.forEach((val, key) => {
      list[key] = Array.from(val)
    })
    
    return list
  }
}

由于它们是私有的，我用 getter 去返回它们，我首先将它们转换为数组和 JavaScript 对象，因为它们更容易也更常用，并且它还能防止从外部更改这些私有值。

接下来，我们需要一种方式去添加顶点。

class Graph {
  ...

  addVertex(vertex = null) {
    if(
     !this.#vertices.has(vertex) &&
     vertex !== null && 
     vertex !== undefined
    ) {
      this.#vertices.add(vertex);
      this.#adjacentList.set(vertex, new Set());
    }
  }

}

所有这些方法所做的，都是确保每个顶点不为空，并且之前没有被添加过。然后将它添加到顶点列表和用一个空的 Set 作为值的映射。

现在我们需要一种方式添加边。

class Graph {
   ...

   addEdge(vertex1 = null, vertex2 = null, directed = true) {
     if(
       vertex1 !== null && vertex1 !== undefined &&
       vertex2 !== null && vertex2 !== undefined && 
       vertex1 != vertex2
     ) {
       this.addVertex(vertex1);
       this.addVertex(vertex2);

       this.#adjacentList.get(vertex1).add(vertex2);

       if(directed) {
         this.#adjacentList.get(vertex2).add(vertex1);
       }
     }
   }
}

这要做的是首先保证两个顶点彼此不同，并且不为空。之后，我们添加他们到顶点列表中，该列表在添加他们之前已经检查这些顶点是否存在列表中。它通过将 vertex2 添加到 vertex1 邻接列表，这意味着 vertex1 连接到 vertex2，如果它是定向的，它也使 vertex2 连接到 vertex1 的双向连接。

有了它，图就有了我们想要、需要的一切。

宽度优先遍历

当你有任何类型的数据结构时，就有搜索这些条目（在本例中为节点）的需求，在图中搜索节点的一种方法是使用宽度优先搜索。

这种搜索或遍历被熟知在树数据结构领域，树遍历就是一种图遍历。

对于这个图，我们将使用颜色的概念来跟踪我们是否完成了对节点邻接表的检查，并避免为了效率而多次访问一个节点。

这个概念很简单，默认情况下所有节点都是绿色的，当您检查一个节点时，它会变成黄色，当您访问它的所有邻近节点时，它会变成红色。

const COLORS = Object.freeze({
  GREEN: 'green',
  YELLOW: 'yellow',
  RED: 'red'
});

当你进行宽度优先遍历时，你检查所有邻接节点，当你检查时，你创建一个队列，队列里面有下一个要检查的节点。

注意: 无论何时提到 检查，它只是表示正在读取节点值。当提到访问时，意味着我们正在检查它的邻接节点列表。

下面的函数取一个我们刚刚实现的图和要开始查找的顶点，以及一个当我们检查节点时将被调用的回调函数。

function breathFirstSearch(graph, fromVertex, callback) {
  const {vertices, adjacentList} = graph;
  
  if(vertices.length === 0) return;
  
  const color = vertices
      .reduce((c, v) => ({...c, [v]: COLORS.GREEN}), {});
  const queue = [];
  
  queue.push(fromVertex);
  
  while(queue.length) {
    const v = queue.shift();
    const nearVertex = adjacentList[v];
    color[v] = COLORS.YELLOW;
    
    nearVertex.forEach(w => {
      if(color[w] === COLORS.GREEN) {
        color[v] = COLORS.YELLOW;
        queue.push(w);
      }
    });
    
    color[v] = COLORS.RED;
    
    callback && callback(v);
  }
}

它从解构顶点和相邻列表开始，它将是一个数组和一个对象，因为这是我们在 getter 中定义的。如果没有顶点，它什么也不做就返回。然后，我们把所有节点都涂成绿色，这基本上是一个顶点到颜色的映射，所以我们可以很容易地查询节点的颜色

队列是为了跟踪下一个要访问的顶点，从一开始，提供的顶点就是第一个要访问的顶点。检查队列数据结构文章以了解它如何工作。

当队列中有一些东西时，我们将移动队列以获取前面的顶点，获取其相邻的节点列表，并将其涂成黄色，因为我们已经检查了它的值。每个循环的顶点都排队等待下一次访问，只要它们是绿色的，我们就把它们涂成黄色。

由于我们检查了所有的顶点相邻列表，我们可以将它涂成红色，因为它已经被完全访问了，并使用它的值调用回调函数。此时，队列中应该有一些内容，如果有，进程将继续。

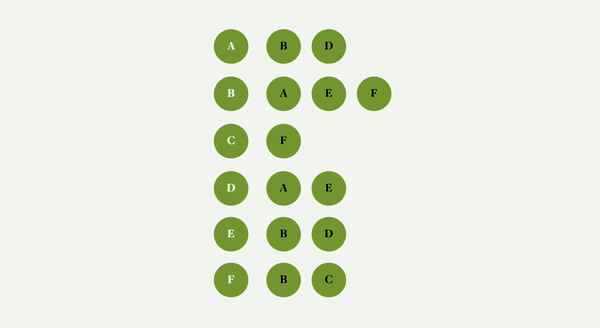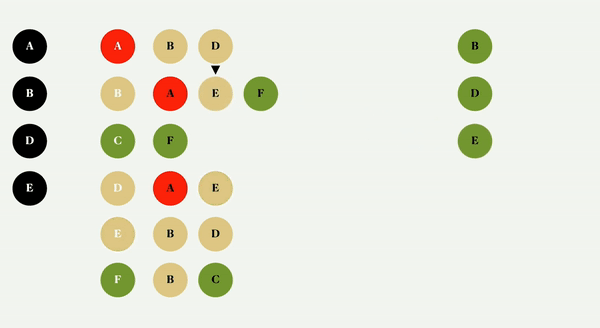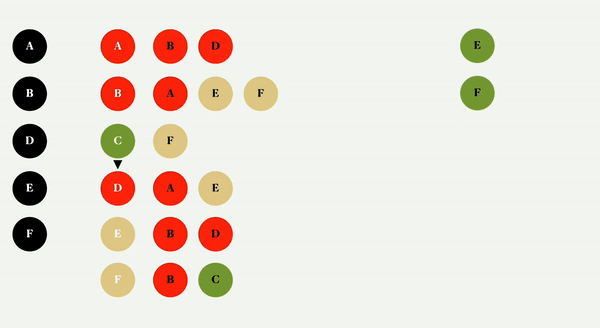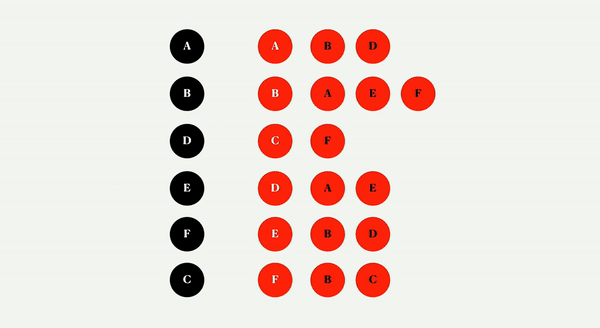
彩色图宽度优先搜索与队列在右边和访问顺序在左边。视频

深度优先遍历

深度优先遍历算法运行有点不同。它不是在访问队列中的下一个节点之前检查所有相邻的列表节点，而是在使用栈数据结构检查该节点以跟踪下一个检查哪个节点时立即访问该节点。

这里使用了相同的颜色概念，他的实现基于递归函数，而不是宽度优先搜索算法中使用的 while 循环。它看起来像这样：

function depthFirstSearch(graph, fromVertex, callback) {
  const {vertices, adjacentList} = graph;
  
  if(vertices.length === 0) return;
  
  const color = vertices
     .reduce((c, v) => ({...c, [v]: COLORS.GREEN}), {});
  
  callback && callback(fromVertex);
  color[fromVertex] = COLORS.YELLOW;
  
  function visit(v) {
    if(color[v] === COLORS.GREEN) {
      callback && callback(v);
      color[v] = COLORS.YELLOW;
      adjacentList[v].forEach(visit);
    }
    color[v] = COLORS.RED;
  }
  
  adjacentList[fromVertex].forEach(visit);
}

该函数接受与宽度优先搜索函数相同的参数，并执行相同的检查和颜色设置。在将所有节点着色为绿色之后，它将调用第一个顶点的回调函数，然后将其着色为黄色，因为此时在检查它。

它声明了一个访问递归函数，用于调用当前每个顶点的邻接节点。这个访问函数检查节点是否为绿色，是否未被检查或访问，调用回调函数，将其着色为黄色，然后抓取相邻的列表，逐个再次调用自己。

只有在检查完所有相邻列表节点及其相邻列表节点之后，它才能将节点着色为红色，以此类推。它在处理节点之前先深入搜索，这就是为什么它被称为深度优先搜索算法。

彩色图深度优先遍历，右边是一个堆栈，左边是访问顺序。视频

查看这篇文章的所有代码

结论

作为一名开发人员，熟悉所有不同的数据结构并理解如何处理数据对你的职业生涯进入下一个阶段至关重要，与此同时，也要能够应用不同的数据结构算法需要不同的思维方式，去解决任何编程问题。

如果发现译文存在错误或其他需要改进的地方，欢迎到 掘金翻译计划 对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划 是一个翻译优质互联网技术文章的社区，文章来源为 掘金 上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注 掘金翻译计划、官方微博、知乎专栏。

avatar
文章
阅读
粉丝