事实上,根据期望的线性性质和样本由独立同分布采样的性质,我们可以写出
S∼DmE[R(h)]=m1i=1∑mS∼DmE[1h(xi)=c(xi)]=m1i=1∑mS∼DmE[1h(x)=c(x)],
对于样本S中的任何x。因此,
S∼DmE[R(h)]=S∼DmE[1{h(x)=c(x)}]=x∼DE[1{h(x)=c(x)}]=R(h).
下面介绍了可能近似正确(PAC)的学习框架.我们用O(n)来表示任意元素x∈X的关于计算表示的成本的一个上限,用大小(c)表示c∈C的计算的最大成本。例如,X可能是Rn中的向量,对于它,基于数组的表示的成本将是O(n)。
定义2.3 PAC学习
一个概念C被认为是PAC可学习的,如果存在算法A和多项式函数poly(.,.,.,.)使得对任何ϵ>0,δ>0,对于X上的所有分布D和任何目标概念c∈C,以下适用于任何样本大小m≥poly(1/ϵ,1/δ,n,size(c)):
S∼DmPr[R(hs)≤ϵ]≥1−δ.
如果A进一步在poly(1/ϵ,1/δ,n,size(c))中运行,则C被认为是有效的 PAC 可学习的。当这样的算法A存在时,它被称为C的 PAC 学习算法。
因此,如果算法在观察1/ϵ和1/δ中的多项式后返回的假设是以高概率(至少1−δ)近似正确(误差最大为 ϵ)的,则概率类C是PAC可学习的,这证明了PAC术语的合理性。δ>0用于定义置信度1−δ。注意,如果算法的运行时间是1/ϵ 和 1/δ的多项式,那么如果算法接收到完整样本,则样本大小m也必须是多项式。
PAC 定义的几个关键点值得强调。首先,PAC 框架是一个无分布模型:没有对从中抽取样本的分布 D 做出特定假设。其次,用于定义误差的训练样本和测试样本是根据相同的分布 D 绘制的。这是在大多数情况下泛化成为可能的必要假设。
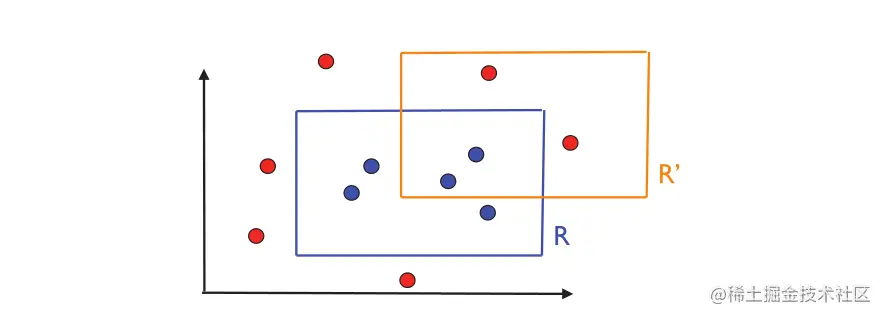
图片2.1 目标概念 R 和可能的假设 R′。圆圈代表训练实例。蓝色圆圈是标记为 1 的点,因为它位于矩形 R 内。其他为红色并标记为 0。
最后,PAC 框架处理概念类C的可学习性问题而不是一个特定的概念。请注意,概念类C是算法已知的,但当然目标概念c∈C是未知的。
在许多情况下,特别是当概念的计算表示没有明确讨论或者很简单时,我们可能会在 PAC 的定义中省略对n和size(c)的多项式依赖,而只关注样本复杂度。
我们现在用一个特定的学习问题来说明 PAC 学习。
示例2.1 学习轴对齐的矩形
考虑实例集是在平面中的点的情况,X=R2,概念集C是位于X=R2中的所有轴对齐矩形的集合。因此,每个概念c是特定轴对齐矩形内的一组点。学习问题包括使用标记的训练样本以较小的误差确定目标轴对齐的矩形。我们将证明轴对齐矩形的概念类是 PAC 可学习的。
图 2.1 说明了这个问题。 R 表示目标轴对齐矩形,R′ 表示假设。从图中可以看出,R′的误差区域由在矩形R内但在矩形R′外的区域和矩形R′内但是在矩形R外的区域构成。第一个区域对应于漏报,即,被R′标记为0或负的点,实际上是正的或被标记为1的点。第二个区域对应于误报,即被R′标记为正但实际上被标记为负的点。
为了表明概念类是 PAC 可学习的,我们描述了一个简单的 PAC 学习算法 A。给定一个标记样本 S,该算法包括返回最紧密的轴对齐矩形 R′ = RS,其中包含标记为 1 的点。图2.2 说明了算法返回的假设。根据定义,RS 不会产生任何误报,因为它的点必须包含在目标概念 R 中。 因此,RS 的误差区域包含在 R 中。
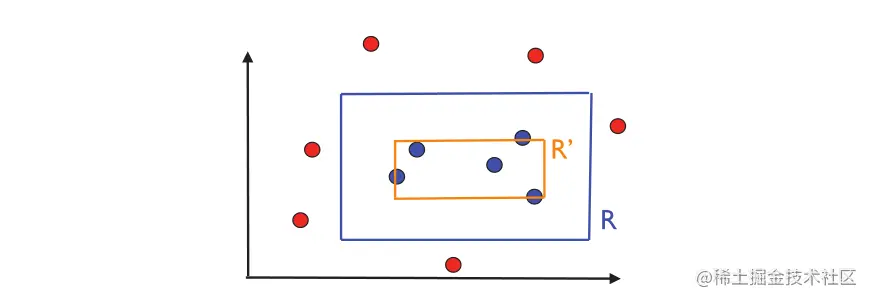
图片2.2 算法返回的假设R′=Rs的图示