强化学习入门2—初识MDP

小菜羊
543 阅读5分钟

本文为强化学习入门系列的第二篇，主要介绍强化学习中非常重要的理论框架——MDP 马尔可夫决策过程。

MDP 马尔可夫决策过程

MDP即Markov Decision Process，马尔可夫决策过程。MDP是强化学习问题的数学化形式，可以说这节开始将接触强化学习的理论部分。

基础概念

什么是强化学习？

有几个概念需先明确。首先是智能体。智能体(agent)表示能进行学习以及实施决策的机器。智能体之外所有与其相互作用的事物都被称作环境(environment)。智能体在环境中，与环境相互交互，在环境的某一时刻的状态(state)中选择动作(action)，环境对动作做出相应的反馈，并在下一时刻转变至新的状态，同时产生一个奖励(reward) 返回给智能体。这就是智能体-环境的一个交互过程。如下图。

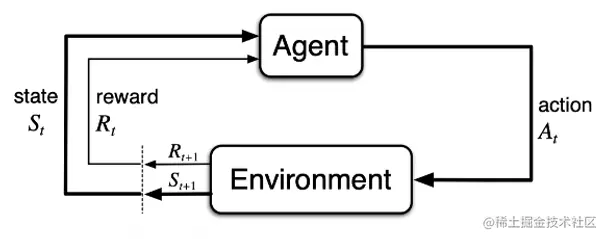
1.1.png

强化学习考虑的就是智能体与环境之间的交互学习，智能体的学习目标就是环境所返回的奖励，而RL任务就是最大化奖励的累积和的期望。是一种无监督下进行主动学习的方法。奖励也是评估动作选择的基础。

MDP

MDP是强化学习的基础，是RL的理论框架。在MDP中，我们考虑状态 SS、动作 AA，奖励 RR。具体来说，智能体在时刻 tt 观察到所处环境状态的某种特征表达 sts_t，接着选择动作 ata_t，下一时刻收到动作 ata_t 的结果即奖励 rt+1r_{t+1}，同时进入下一状态 st+1s_{t+1}。而当MDP中的状态、动作、奖励集合 (S、A、R)(S、A、R) 都只有有限个元素，这样的MDP也称为有限MDP。形式化的序列如下：

(s0,a0,r0,...,st,at,rt,...)(s_0,a_0,r_0,...,s_t,a_t,r_t,...)

四参数表达式

p(s′,r∣s,a)=P(St=s′,Rt=r∣St−1=s,At−1=a)p(s',r|s,a)=P(S_{t}=s',R_{t}=r|S_{t-1}=s,A_{t-1}=a)

下面是一个小结：

Process(s0,s1,s2,...,st,...)  with  P(st∣st−1,...,s0)Markov Process(s0,s1,s2,...,st,...)  with  P(st∣st−1,...,s0)=P(st∣st−1)Markov Process(s0,r0,s1,r1,s2,r2,...,st,rt,...)  with  P(st∣st−1,...,s0)=P(st∣st−1)Markov Decision Process(s0,a0,r0,s1,a1,r1,...,st,at,rt,...)  with  P(st∣st−1,...,a0,,s0)=P(st∣st−1,at−1)\begin{aligned} &\text{Process} \\ &\quad(s_0,s_1,s_2,...,s_t,...)\;\text{with}\; P(s_t|s_{t-1},...,s_0)\\ &{\text{Markov Process}}\\ &\quad(s_0,s_1,s_2,...,s_t,...)\;\text{with}\; P(s_t|s_{t-1},...,s_0)=P(s_t|s_{t-1})\\ &\text{Markov Process}\\ &\quad(s_0,r_0,s_1,r_1,s_2,r_2,...,s_t,r_t,...)\;\text{with}\; P(s_t|s_{t-1},...,s_0)=P(s_t|s_{t-1})\\ &\text{Markov Decision Process}\\ &\quad(s_0,a_0,r_0,s_1,a_1,r_1,...,s_t,a_t,r_t,...)\;\text{with}\; P(s_t|s_{t-1},...,a_0,,s_0)=P(s_t|s_{t-1},a_{t-1})\\ \end{aligned}

上面的概率等式表明，MDP中，st、rts_t、r_t 的每个可能的值的概率只取决于前一个状态和动作 st−1、at−1s_{t-1}、a_{t-1} ，与更早之前的状态和动作无关。这样的状态也因此称具有马尔可夫性。

对于连续性任务，定义G为奖励的加权和：

Gt=Rt+1+γRt+2+γ2Rt+3+...=∑k=0∞γkRt+k+1=Rt+1+γGt+1\begin{aligned} G_t=&R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3}+...=\sum_{k=0}^{\infty}\gamma^k R_{t+k+1}\\ =&R_{t+1}+\gamma G_{t+1} \end{aligned}

γ\gamma 称为折扣因子。

实际上总奖励 GtG_t 仍是有限的，因为只要奖励是非零常数且 γ>1\gamma>1，总奖励 GtG_t 是可以收敛的，比如当奖励是常数1时，可以表示为

Gt=∑k=0∞γk=11−γG_t=\sum_{k=0}^{\infty}\gamma^k=\dfrac{1}{1-\gamma}

状态价值函数与动作价值函数

策略（policy）从状态到每个动作的选择概率的映射，也就是智能体选择动作的随机函数。用 π\pi 表示。π\pi 和 ss 是绑定的。π(a∣s)\pi(a|s) 表示状态s下选择动作a的概率，π(s)\pi(s) 是指在该状态下（也就是该时刻下）的概率密度函数。π(s)\pi(s) 是一个函数，π(a∣s)\pi(a|s) 才是一个具体的概率值。

不同策略下的状态的价值函数不同，所以我们用 vπ(s)v_{\pi}(s) 表示策略 π\pi 下状态 ss 的价值函数。相同策略相同状态下采取不同的动作所得到的价值也不同，故用 qπ(s,a)q_{\pi}(s,a) 表示策略 π\pi 下在状态 ss 下采取动作 aa 的价值函数。vπv_{\pi} 也称为策略 π\pi 的状态价值函数，qπq_{\pi} 也称为策略 π\pi 的动作价值函数。不同策略下采取相同动作的概率可能不同。

对所有的状态 ss，当前状态的价值就是从状态s开始，给定策略 π\pi，智能体根据当前策略执行动作所得到的奖励的概率期望值。这里求期望是因为从 ss 进入到下一状态 s′s' 时，采取不同的动作进入不同的s′s'，所获得的奖励也不一样，所以要对所有可能的 s′s' 求期望。

vπ(s)=Eπ[Gt  ∣  St=s]=Eπ[∑t=0∞γkRt+k+1  ∣  St=s]\begin{aligned} v_{\pi}(s)=& E_{\pi}[G_t\;|\;S_t=s]= E_{\pi}[\sum_{t=0}^{\infty}\gamma^k R_{t+k+1}\;|\;S_t=s] \end{aligned}

同样，对于动作价值函数 qπq_{\pi}，即给定策略 π\pi，执行动作a后，因为不同的动作环境产生的奖励可能不同，所以要对所有可能的决策序列的奖励求期望，我们有

qπ(s,a)=Eπ[Gt  ∣  St=s,At=a]=Eπ[∑t=0∞γkRt+k+1  ∣  St=s,At=a]\begin{aligned} q_{\pi}(s,a)=& E_{\pi}[G_t\;|\;S_t=s,A_t=a]= E_{\pi}[\sum_{t=0}^{\infty}\gamma^k R_{t+k+1}\;|\;S_t=s,A_t=a] \end{aligned}

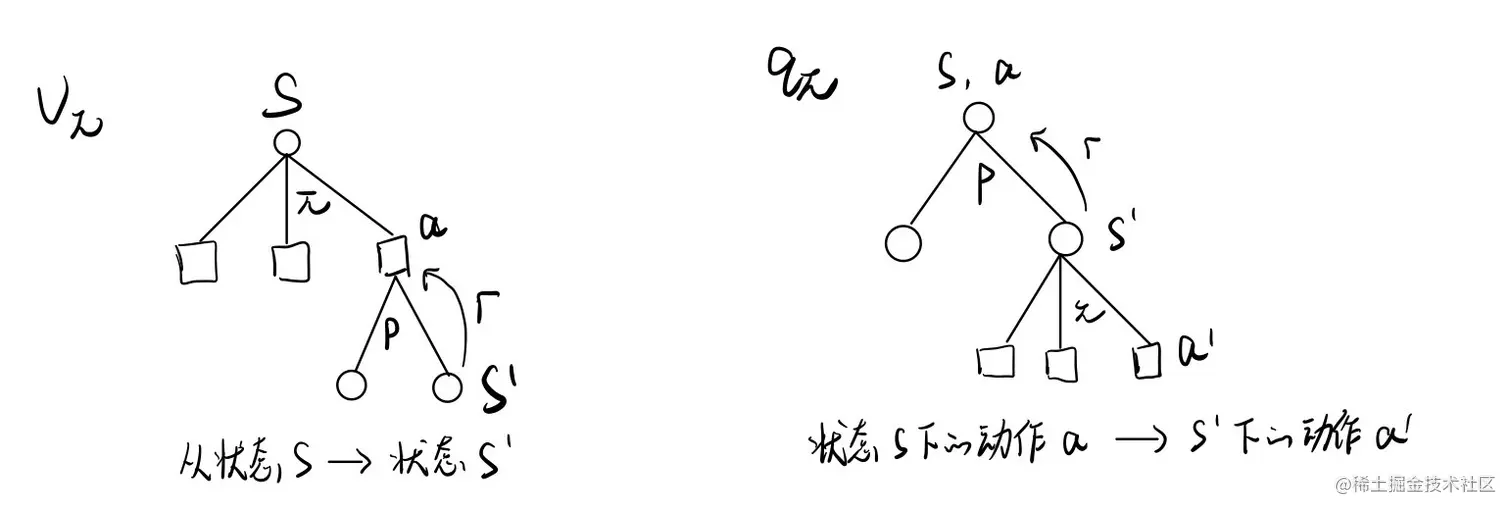
结合图来理解，可以看到，vπv_{\pi} 是从状态到状态的reward期望，qπq_{\pi} 是从动作到动作的reward的期望。而概率 pp 是环境决定的，所以我们只能优化策略。 2021_7_1.jpg

其实，不难发现 vπv_{\pi} 与 qπq_{\pi} 有如下关系：

vπ(s)=Ea∼A(s)[qπ(s,a)]=∑aπ(a∣s)qπ(s,a)v_{\pi}(s)=E_{a\sim A(s)}[ q_{\pi}(s,a)]=\sum_a \pi(a|s) q_{\pi}(s,a)

观察式子可以发现，状态的价值等于该状态下所有可能的动作的价值，乘以当前策略下选择可能的动作的概率的期望。而动作的价值取决于后继奖励的期望值以及其余奖励的总和的期望值。

其实 qπ(s,a)q_{\pi}(s,a) 还可以写成：

qπ(s,a)=E[Rt+1+γ⋅vπ(St+1)  ∣  St=s,At=a]=∑s′,rp(s′,r∣s,a)[r+γvπ(s′)]q_{\pi}(s,a)=E[R_{t+1}+\gamma \cdot v_{\pi}(S_{t+1})\;|\;S_t=s,A_t=a] =\sum_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]

进一步的，对于任何策略 π\pi 和任何状态 ss ，我们可以得到，状态 ss 当前的价值与其可能的后继状态 s′s' 之间的关系：

vπ(s)=Eπ[Rt+1+γGt+1  ∣  St=s]=∑aπ(a∣s)∑s′∑rp(s′,r∣s,a)[r+γEπ[Gt+1  ∣  St+1=s′]=∑aπ(a∣s)∑s′,rp(s′,r∣s,a)[r+γvπ(s′)]\begin{aligned} v_{\pi}(s) =& E_{\pi}[R_{t+1}+\gamma G_{t+1}\;|\;S_t=s] \\ =&\sum_a \pi(a|s)\sum_{s'}\sum_{r}p(s',r|s,a)[r+\gamma E_{\pi}[G_{t+1}\;|\;S_{t+1}=s'] \\ =&\sum_a \pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')] \\ \end{aligned}

该方程也叫贝尔曼方程（Bellman equation）。因为pp是概率密度函数，所以最后一项其实就是期望值，也就是 qπq_{\pi}。

贝尔曼最优方程

如何推导？

我们知道贝尔曼方程，其实就是状态价值函数的递归形式：

vπ(s)=∑aπ(a∣s)∑s′,rp(s′,r∣s,a)[r+γvπ(s′)]v_{\pi}(s)=\sum_a \pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_{\pi}(s')]

怎么找最优的策略？

实际上最优的策略（记作 π∗\pi_* ）可能不止一个，但他们一定共享最优的动作价值函数以及状态价值函数，所以有：

v∗(s)=max⁡πvπ(s)q∗(s,a)=max⁡πqπ(s,a)v_*(s)=\max_{\pi} v_{\pi}(s) \\ q_*(s,a)=\max_{\pi} q_{\pi}(s,a)

最优策略下，各个状态的价值一定等于这个状态下最优动作的期望奖励（因为策略已经确定了），有：

v∗(s)=max⁡a∈A(s)qπ∗(s,a)=max⁡aEπ∗[Gt∣St=s,At=a]=max⁡aEπ∗[Rt+1+γGt+1∣St=s,At=a]=max⁡aE[Rt+1+γv∗(St+1)∣St=s,At=a]=max⁡a∑s′,rp(s′,r∣s,a)[r+γv∗(s′)]\begin{aligned} v_*(s)=&\max_{a\in A(s)} q_{\pi_*}(s,a) \\ =&\max_a E_{\pi_*}[G_t|S_t=s,A_t=a] \\ =&\max_a E_{\pi_*}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a] \\ =&\max_a E[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s,A_t=a] \\ =&\max_a\sum_{s',r}p(s',r|s,a)[r+\gamma v_*(s')] \end{aligned}

这就是状态价值函数的贝尔曼最优方程。

而对于动作价值函数，其贝尔曼最优方程如下：

q∗(s,a)=E[Rt+1+γmax⁡a′q∗(St+1,a′)  ∣  St=s,At=a]=∑s′,rp(s′,r∣s,a)[r+γmax⁡a′q∗(s′,a′)]\begin{aligned} q_{*}(s,a)=&E[R_{t+1}+\gamma \max_{a'}q_*(S_{t+1},a')\;|\;S_t=s,A_t=a] \\ =& \sum_{s',r}p(s',r|s,a)[r+\gamma \max_{a'}q_*(s',a')] \end{aligned}

参考

  1. sutton.Barto.《强化学习（第二版）》
avatar
文章
阅读
粉丝