WebGL第十八课：拉伸的矩阵表达(涉及数学推导)｜ 8月更文挑战

这是我参与8月更文挑战的第4天，活动详情查看：8月更文挑战

本文标题：WebGL第十八课：拉伸的矩阵表达(涉及数学推导)｜ 8月更文挑战

引子

前面两次课，我们分别讲了向量位移和向量拉伸，两个操作，我们知道，进行这两个操作之后，会得出新的向量。

那好，我们给出一个向量A：

$\left(\begin{array}{cc} 1\\ 2\end{array}\right)$

然后再给出一个向量B:

$\left(\begin{array}{cc} 2\\ 4\end{array}\right)$

诸位，请问，由A到B，是进行了什么操作？

通过位移 将A转换成B

如果是位移操作，我们必须得出，进行了多少的位移。

很简单，用向量减法：

$B - A = \left(\begin{array}{cc} 2\\ 4\end{array}\right) - \left(\begin{array}{cc} 1\\ 2\end{array}\right) = \left(\begin{array}{cc} 1\\ 2\end{array}\right)$

我们得出，A经过位移 $\left(\begin{array}{cc} 1\\ 2\end{array}\right)$可以得到B。

通过拉伸 将A转换成B

如果是拉伸的话，我们也需要得到一个拉伸系数才行。

也就是

$A * x = B$

我们需要知道上面式子中的 $x$。

我们通过口算，可以得出：

$A*2 = \left(\begin{array}{cc} 1\\ 2\end{array}\right) * 2 = \left(\begin{array}{cc} 2\\ 4\end{array}\right)$

那么 $x = 2$。

两种操作的辩证

我们发现，A到B的转变，竟然可以通过两种操作都行，并不是唯一的。

是的，对于单个向量来说，转换成另一个向量确实可以有多种途径。

但是，对于一堆向量转换成另一对向量，这个转换的操作就不一定了，往往是固定的。

例如下图：

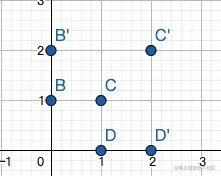
我们观察$BCD$三个点，转换成$B' C' D'$这三个点的过程：

• 看$B$, 既可以认为是拉伸2倍，也可以认为是向上经过一个位移
• 看$C$, 既可以认为是拉伸2倍，也可以认为是向右上方进行一个位移
• 看$D$, 既可以认为是拉伸2倍，也可以认为是向右进行一个位移

结论就是：

对于一堆向量来说，往往只能通过某一种操作转换成另一个向量。

上面的结论很重要，因为我们在游戏行业，一个模型往往有很多的点，我们基于我们的业务需求，例如位移，拉伸，旋转等等，必须把这些点，通过某些操作变成另外一些点。核心就是，所有的点，所经历的操作必须完全一致。不能说，某些点是拉伸了，某些点是位移了，那就乱套了。

我们下面开始正式推导如何用矩阵来表达拉伸操作。

推导矩阵：x拉伸2倍，y拉伸3倍

有向量$A$ :

$\left(\begin{array}{cc} x\\ y\end{array}\right)$

矩阵 $D$:

$\begin{bmatrix} a & c \\ b & d \end{bmatrix}$

我们的结果是$A$的$x$坐标变成$2$倍，$A$的$y$坐标变成$3$倍，如下：

然后：D * A = $\left(\begin{array}{cc} 2x\\ 3y\end{array}\right)$ 。

即：

$\begin{bmatrix} a & c \\ b & d \end{bmatrix}$ * $\left(\begin{array}{cc} x\\ y\end{array}\right)$ = $\left(\begin{array}{cc} 2x\\ 3y\end{array}\right)$

--->(我们以前就说过，矩阵乘法就是，向量线性组合，这一步不懂的可以看前面的课程)

$\left(\begin{array}{cc} a\\ b\end{array}\right) * x + \left(\begin{array}{cc} c\\ d\end{array}\right) * y = \left(\begin{array}{cc} 2x\\ 3y\end{array}\right)$

问题来了：

我们现在需要求出 $\left(\begin{array}{cc} a\\ b\end{array}\right)$是什么，$\left(\begin{array}{cc} c\\ d\end{array}\right)$是什么。

由于A点$\left(\begin{array}{cc} x\\ y\end{array}\right)$是任意的，我们可以随便给几个坐标进去，然后联立解方程组，然后就可以得出相应的结果，我要说的是，最方便的取的A点就是两个就是

$\left(\begin{array}{cc} 1\\ 0\end{array}\right)$和$\left(\begin{array}{cc} 0\\ 1\end{array}\right)$

我们试试$\left(\begin{array}{cc} 1\\ 0\end{array}\right)$：

$\left(\begin{array}{cc} a\\ b\end{array}\right) * 1 + \left(\begin{array}{cc} c\\ d\end{array}\right) * 0 = \left(\begin{array}{cc} 2\\ 0\end{array}\right)$

--->

$\left(\begin{array}{cc} a\\ b\end{array}\right) * 1 = \left(\begin{array}{cc} 2\\ 0\end{array}\right)$

--->

$\left(\begin{array}{cc} a\\ b\end{array}\right) = \left(\begin{array}{cc} 2\\ 0\end{array}\right)$

结果得出来了！

我们再试试$\left(\begin{array}{cc} 0\\ 1\end{array}\right)$

$\left(\begin{array}{cc} a\\ b\end{array}\right) * 0 + \left(\begin{array}{cc} c\\ d\end{array}\right) * 1 = \left(\begin{array}{cc} 0\\ 3\end{array}\right)$

--->

$\left(\begin{array}{cc} c\\ d\end{array}\right) * 1 = \left(\begin{array}{cc} 0\\ 3\end{array}\right)$

--->

$\left(\begin{array}{cc} c\\ d\end{array}\right) = \left(\begin{array}{cc} 0\\ 3\end{array}\right)$

哈哈，又得出来了！

也就是说：

$\left(\begin{array}{cc} 2\\ 0\end{array}\right) * x + \left(\begin{array}{cc} 0\\ 3\end{array}\right) * y = \left(\begin{array}{cc} 2x\\ 3y\end{array}\right)$

即：

$\begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}$ * $\left(\begin{array}{cc} x\\ y\end{array}\right)$ = $\left(\begin{array}{cc} 2x\\ 3y\end{array}\right)$

至此，拉伸操作的正式表达矩阵就推出来了，我们给出一般式子：

平面中的任一点A，向量表达式： $\left(\begin{array}{cc} x\\ y\end{array}\right)$, x坐标变成原来的a倍，y坐标变成原来的b倍，用矩阵来表达就是：

$\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}$ * $\left(\begin{array}{cc} x\\ y\end{array}\right)$ = $\left(\begin{array}{cc} a*x\\ b*y\end{array}\right)$

这个结论的推导过程，要详细看一遍，因为后面即将要讲的旋转推导也是这样的。

---

---

---

正文结束，下面是答疑

小能能说，越看上面的式子，然后越联想线性组合，我就越能明白，为什么矩阵乘法用线性组合的观念来思考最舒服。

• 答：对，大家一定要像小能能这样，去用线性组合的思维来理解矩阵乘法。