今天听莫老师讲了姚期智提出的百万富翁问题，简直神了，这也太厉害了吧，我觉得是和零知识证明一样的神奇，或许这就是数学的魅力吧。在不泄露个人隐私的情况下，可以比较两个富翁的财富大小。着实太强了，佩服，其实归根结底都是数学，学好数学的重要性不言而喻，加油吧好好学习数学！

下面个我将从初学者的角度，来写明白《百万富翁》的问题，同时下方也有姚期智老师的论文下载地址，需要的自取。

1、百万富翁问题：

首先我们假设有两个富翁 A 和 B ，且 A 和 B 的财产都在同一水平，设 A 有 i 亿，B 有 j 亿，$0<i,j<=10$。那么下面开始财富大PK。

首先初始化：A 有一个公钥$PK_A$和私钥$SK_A$，加密函数 E 和解密函数 D ，B 知道 A 的公钥但不知道私钥。

1）B 要做到事情：

1. 首先 B 拿出一个随机大数 x ，然后用 A 的公钥加密得到$k=E(x, PK_A)$，相应的 $x=D(k, SK_A)$
2. 计算出$m=k-j+1$，将 m 发送给 A。

2）A 要做的事情：

1. 计算出$k-j+1,k-j+2,\cdots,k-j+j,\cdots,k-j+10$，因为$m=k-j+1$，所以等价于计算$m,m+1,\cdots,k,\cdots,m+9$，你会发现$k-j$从加 1 到加 10 中必然会加上 j 的，因为$j\subseteq(0, 10]$。
2. 然后使用 A 的私钥，$y=D(m, SK_A)$，解密出$m,m+1,\cdots,k,\cdots,m+9$的值分别为$y_1, y_2,\cdots,y_j，\cdots,y_{10}$。
3. 对$y_n$进行求模运算，$z_n=y_n\mod\ p$，其中 p 是 A 随机生成的一个素数，得出集合 $\{z_n\}=z_1, z_2,\cdots,z_i,\cdots,z_j,\cdots,z_{10}$，如果这个集合中至少有两个是不一样的，则进行下一步，反之则重新生成素数p，重复第三步。
4. 之后，保持$z_1,\cdots,z_i$不变，$z_{i+1},\cdots,z_{10}$都加1，就变成$z_1,z_2,\cdots,z_i,z_{i+1}+1,\cdots,z_9+1,z_{10}+1$，然后 A 将该集合和素数 p 发送给 B 。

3）最后的结果：

1. 如果 $x\mod p=z_j$，说明$z_j\subseteq\{z_1,\cdots,z_i\}$，推出$j<=i$。
2. 如果$x\mod p=z_j$，则说明$z_j\subseteq\{z_{i+1}+1,\cdots,z_{10}+1\}$，推出$j>i$。
3. 最后由 B 告诉 A ，到底谁才是最有钱的。

证明完毕，但是我还是有点疑问就是，这个(3).1，$j<=i$的情况下，还是判断不出来谁最有钱呀？

2、小例子

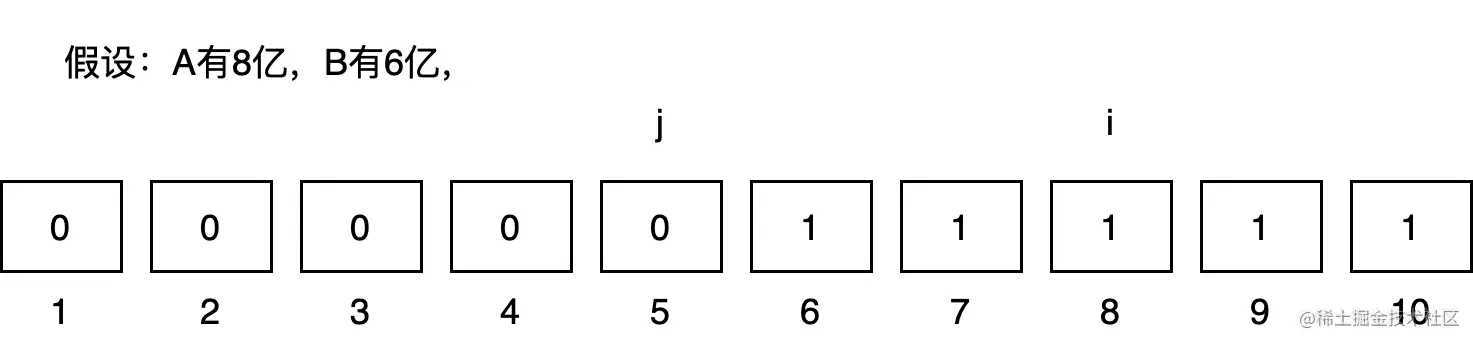
首先生成 10 个箱子，序号从$1,2,3,\cdots,10$，A 有 i 亿，B 有 j 亿，$0<i,j<=10$。

• 然后 B 首先将找到第 j 个箱子
• 设置$1, 2,\cdots,j$号箱子设置为0，$j+1, j+2,\cdots,10$号箱子设置为1。
• 然后轮到 A 找到第 i 箱子，如果箱子的值为0，则$j\geq i$，反之为1，则$j \leq i$。

总结：

姚期智老师在1986年就发表了这个论文，当时互联网处于发展阶段，隐私问题也就没多少人重视，姚老师很有前瞻性，不亏是首位获得图灵奖的华人。但是如今开始重视隐私问题了，滴滴就是前车之鉴，国家也很重视信息安全的建设，所以好好学习吧，哈哈😄