概述

从上一节（什么是神经网络）中我们得知：神经网络是一个函数，它由神经元组成，而神经元也是一个函数。

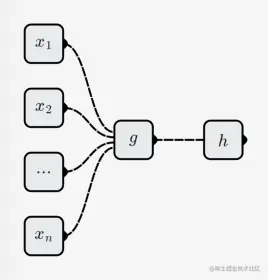
神经元可以继续拆分成2个子函数：

• $n$元线性函数: $g(x_1, ..., x_n)$
• $1$元非线性函数: $h(x)$

神经元所代表的函数为：

$f(x_1, ..., x_n) = h(g(x_1, ..., x_n))$

线性函数$g(x_1, ..., x_n)$

线性函数有如下形式：

$g(x_1, ..., x_n) = w_1x_1 + ..., w_nx_n + b$

其中$w_1, ..., w_n, b$都是参数，不同的线性函数有不同的参数。

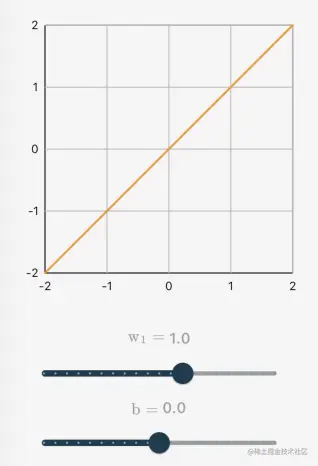
一元线性函数

当$n=1$时，$g(x_1)=w_1x_1 + b$，其函数图像为一条直线：

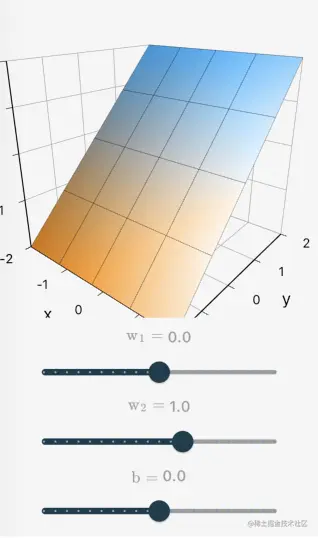
二元线性函数

当$n=2$时，$g(x_1, x_2)=w_1x_1 + w_2x_2+ b$，其函数图像为一个平面：

$n$元线性函数

当$n>2$时，其函数图像为一个超平面。超过了三维，就不方便可视化了。不过大家可以想象，其特点就是直的。

非线性函数$h(x)$

从名字上就很容易理解，非线性函数就是跟线性函数不一样的函数。线性函数是直的，非线性函数就是弯的。如最常见的Sigmoid函数:

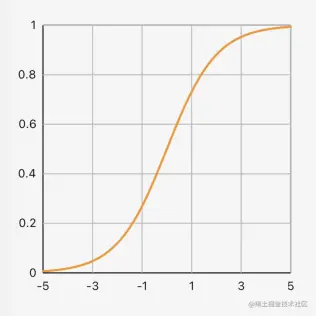
激活函数

在神经网络中，我们把这个非线性一元函数叫做激活函数。一些常见的激活函数可参考知识库中的激活函数，其中：

• Linear: $f(x)=x$是一个线性函数，代表不使用非线性函数的情况
• Softmax 是个特例。严格来讲，它不算激活函数

必要性

为什么要在线性函数后面跟一个非线性的激活函数呢？

这是因为：

1. 如果神经元都是线性函数，那么由神经元构成的神经网络也是一个线性函数。

如下面这个例子：

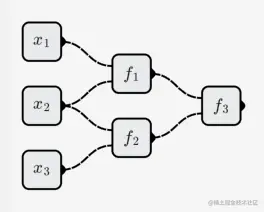
• $f_1(x, y) = w_1x + w_2y + b_1$
• $f_2(x, y) = w_3x + w_4y + b_2$
• $f_3(x, y) = w_5x + w_6y + b_3$

那么整个神经网络所代表的函数为:

$f_3(f_1(x_1, x_2, x_3), f_2(x_1, x_2, x_3))$

$= w_5(w_1x_1 + w_2x_2 + b_1) + w_6(w_3x_2 + w_4x_3 + b_2) + b_3$

$= (w_1w_5)x_1 + (w_2w_5 + w_3w_6)x_2 + (w_4w_6)x_3 + (w_5b_1 + w_6b_2 + b_3)$

这是一个三元的线性函数。

2. 我们需要构造的目标函数包含各式各样的函数，线性函数只是其中一种。

我们希望神经网络能够模拟任意函数，而不只是线性函数。因此我们增加了一个非线性的激活函数，对线性函数进行了"弯曲"。

完整的神经元

完整的神经元融合了线性函数与非线性的激活函数，变得更有趣、更强大了。

一元函数

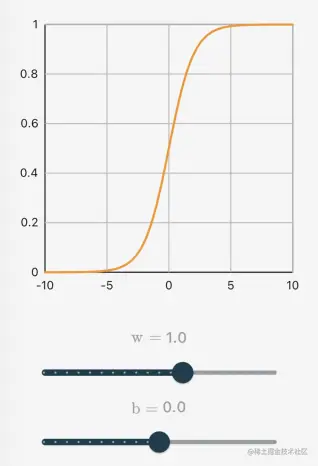
当$n=1$时，$g(x_1)=w_1x_1 + b$，使用Sigmoid激活函数，神经元对应的函数为：

$h(g(x))=\text{sigmoid}(wx + b)$

其函数图像为：

二元函数

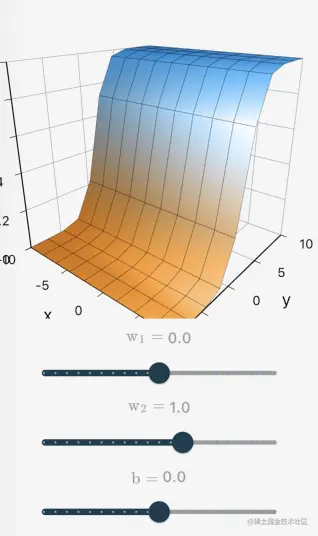
当$n=2$时，$g(x_1, x_2)=w_1x_1 + w_2x_2+ b$，使用Sigmoid激活函数，神经元对应的函数为：

$h(g(x))=\text{sigmoid}(w_1x_1 + w_2x_2 + b)$

其函数图像为：

$n$元函数

由于可视化问题，此处完全靠自己想象！😥

问题

为什么神经元的组合可以模拟复杂函数？

可以直观地想象一下，如何通过简单的神经元模拟稍微复杂一点的函数。

参考软件

可交互版，请参考App： 神经网络与深度学习