2021-07-05算法题

1. 实现strStr() 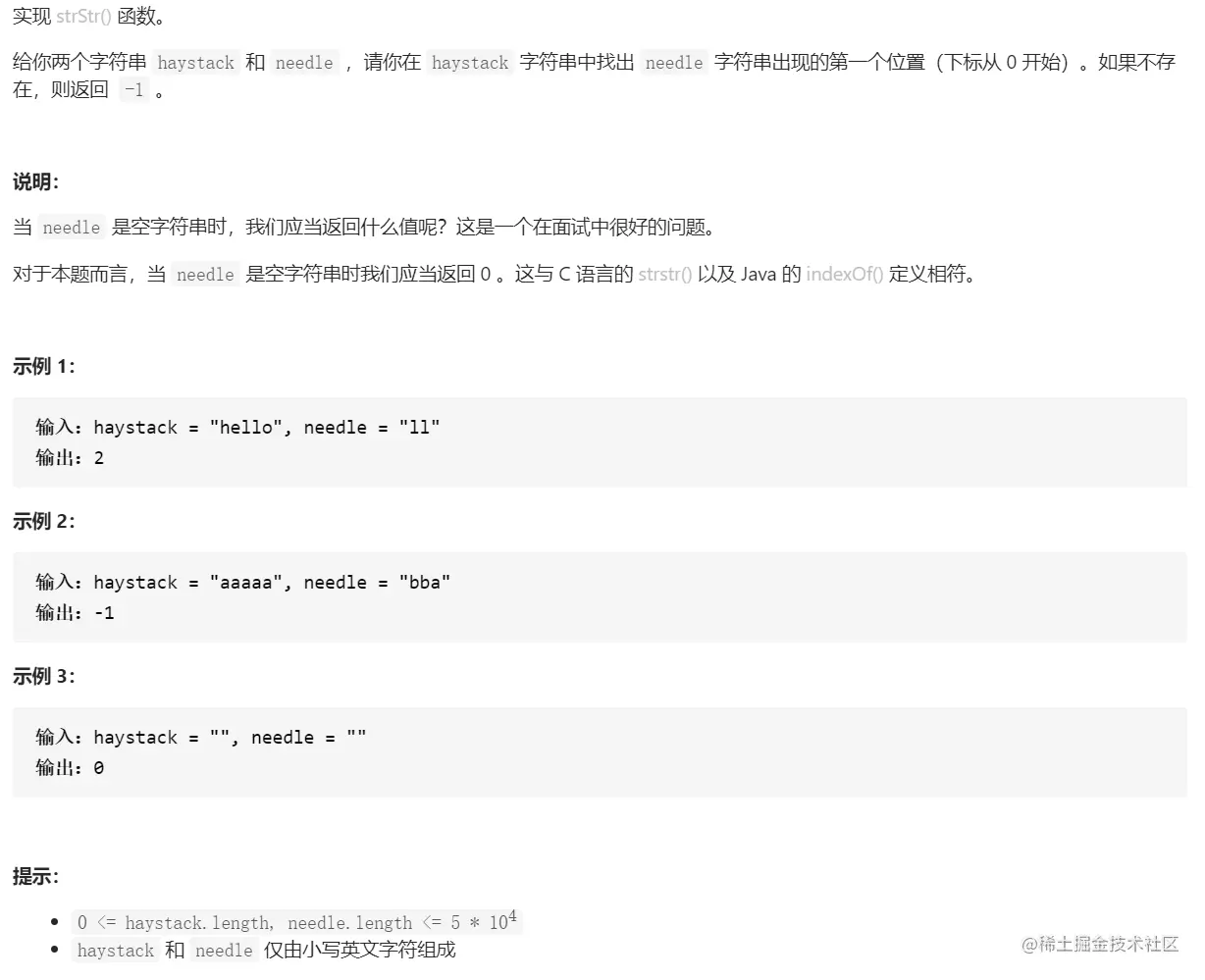思路：暴力匹配：将needle与haystack中所有字串均进行匹配即可

class Solution {
    public int strStr(String haystack, String needle) {
        int index1 = 0;
        int index2 = 0;
        if (needle.length() == 0) {
            return 0;
        } else {
            for (int i = 0; i < haystack.length(); i++) {
                index1 = i;
                while (index1 < haystack.length() && index2 < needle.length()) {
                    if (haystack.charAt(index1) == needle.charAt(index2)) {
                        index1++;
                        index2++;
                    } else {
                        index2 = 0;
                        break;
                    }
                }
                if (index2 == needle.length()) {
                    return i;
                } else if (index1 == haystack.length()) {
                    return -1;
                }
            }
            return -1;
        }
    }
}

2. 搜索插入位置 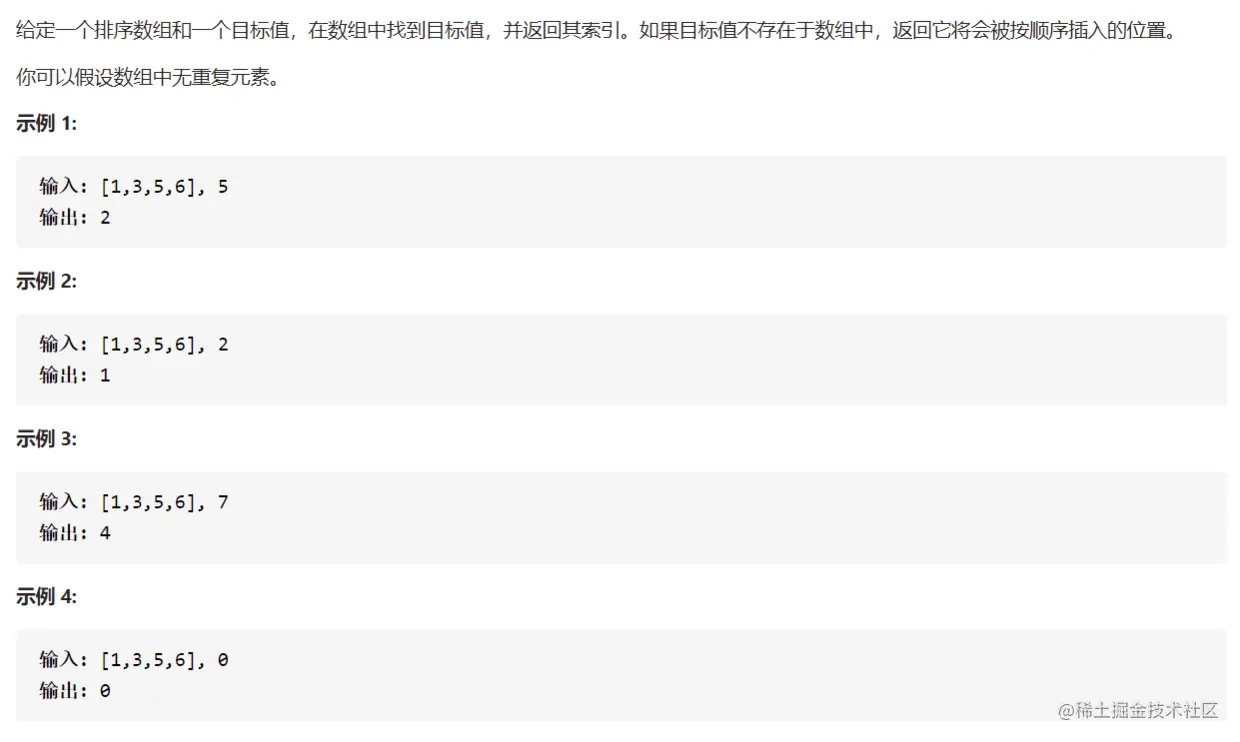思路：当target大于nums[pos]所指元素时pos++，循环结束后的位置即为插入位置（注意在while中要判断pos是否越界）

class Solution {
    public int searchInsert(int[] nums, int target) {
        int pos = 0;
        if (nums.length == 0) {
            nums[0] = target;
            return 0;
        }
        while (target > nums[pos]) {
            pos++;
            if (pos == nums.length) {//注意判断是否越界
                return nums.length ;
            }
        }
        return pos;
    }
}

3. 最大子序和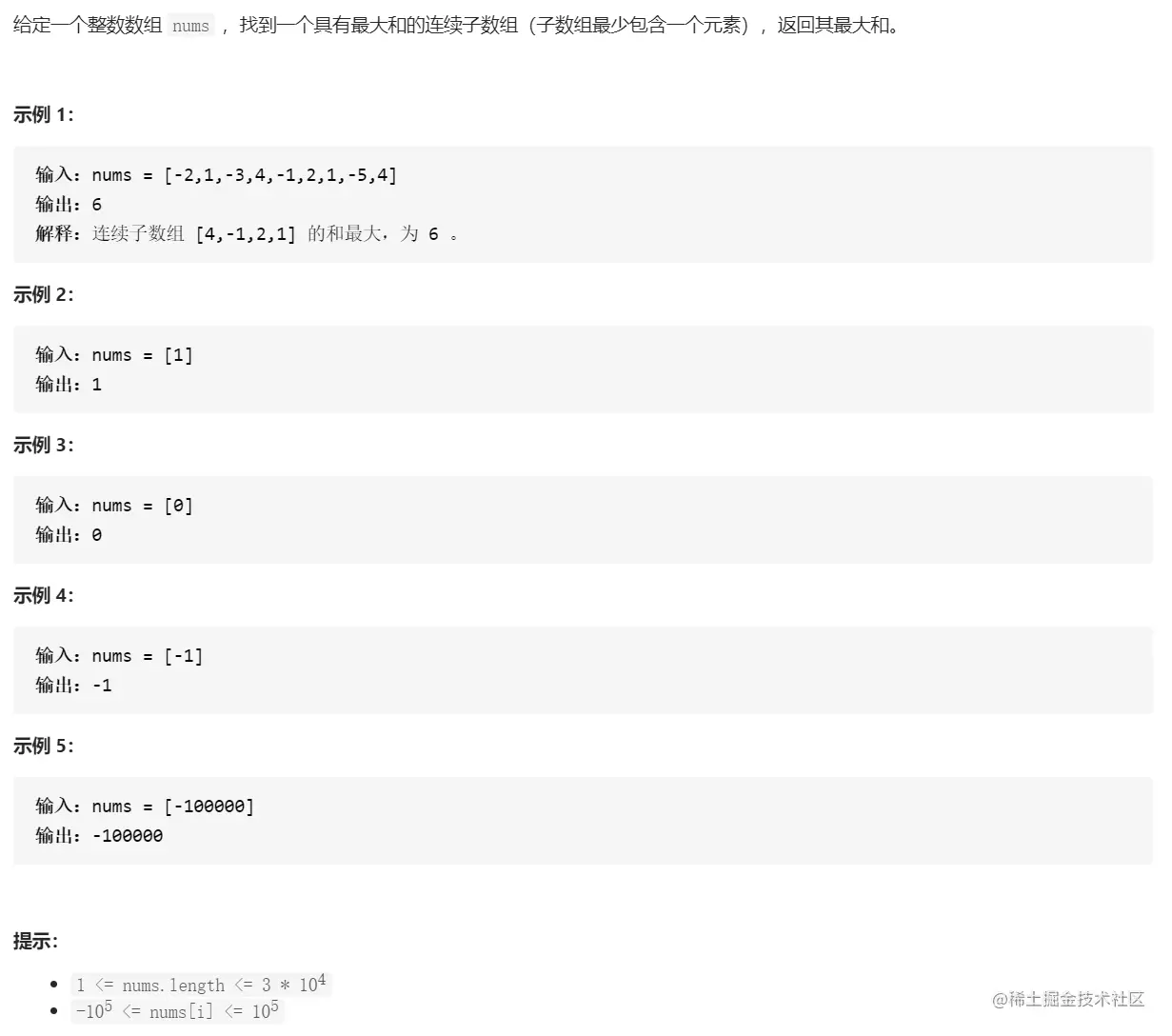（*） 思路：记f(i)为第i个数结尾的最大子序和，用一个变量sum来维护对于当前f(i)的f(i-1)值是多少。sum为sum+nums[i]与nums[i]中最大的那一个

class Solution {
    public int maxSubArray(int[] nums) {
        int sum = nums[0];
        int max = nums[0];
        if (nums.length == 1) {
            return nums[0];
        }
        for (int i = 1; i < nums.length; i++) {
            sum = Math.max(sum + nums[i], nums[i]);
            if (sum > max) {
                max = sum;
            }
        }
        return max;
    }
}