数据降维即将多维数据降为低维,代表性的方法有主成因分析(PCA,principal component analysis)、局部线性嵌入(LLE,locally linear embedding)和拉普拉斯特征映射(Laplacian eigen-map)。
主成因分析(PCA)
在介绍PCA之前,首先需要了解一些线性代数的基本概念:
特征值与特征向量
对于一个n阶矩阵A和实数λ,如果能找到一个非零向量x满足:
则将λ称为A的特征值,x称为A的特征向量。
从几何意义上来说,对于矩阵A,存在一些向量x,使得Ax和x的方向没有发生变化,只有长度发生了变化,长度发生的变化可以用系数λ来度量。
协方差矩阵
协方差
协方差用于衡量两个变量间的误差,方差是协方差的一种特殊情况(两个变量一致时),方差用于衡量单个随机变量的离散程度,其公式如下所示:
σx2=n−11i=1∑n(xi−xˉ)2
协方差则度量两个随机变量的相似程度(变化趋势),其公式如下:
σ(x,y)=n−11i=1∑n(xi−xˉ)(yi−yˉ)
Cov(X,Y)=E[(X−μx)(Y−μy)]
协方差的计算中,两个变量和自身的期望做差再相乘,当两个变量的取值都大于/小于自身期望时,计算得到的协方差为正值,即两个变量的变化趋势相同,反之若一大一小,则协方差为负值。因此协方差可以反映变量间的相关程度。
在现实中描述一个物体的特征通常是多维的,如描述一个人会包括他的身高、性别、体重等等。在对多维数据进行分析时,就需要协方差矩阵来描述,例如对于2维数据,任意两个维度间求其协方差,则可以得到一个包括4个协方差的协方差矩阵:
Σ=[σ(x,x)σ(y,x)σ(x,y)σ(y,y)](2)
可以看到,主对角线上的元素实际为两个维度的方差(特殊的协方差)。下图为4个不同协方差矩阵的数据分布情况:
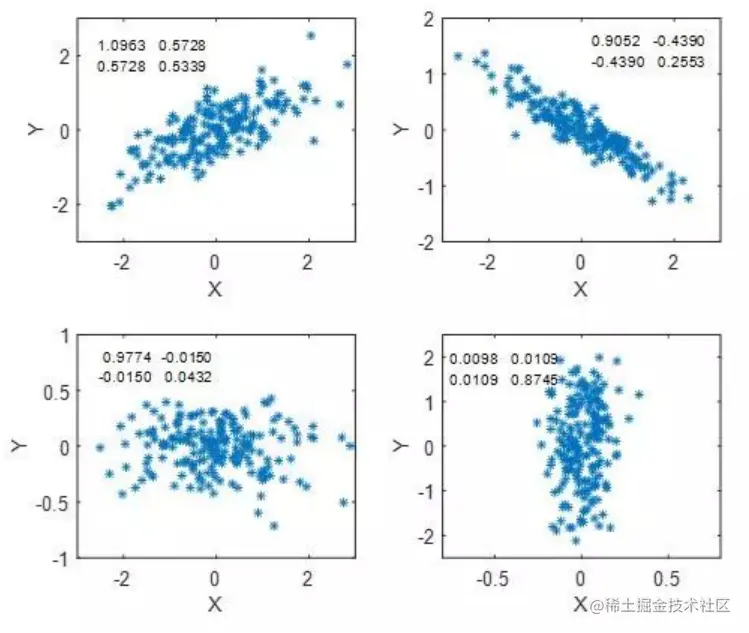
主对角线上的值表示数据在x和y方向的离散程度,值越小越集中。而σ(x,y)和σ(y,x)的正负以及值的大小决定了x与y的相关性,协方差的绝对值越大,相关关系越明显。
PCA基本原理
PCA的主要目的是将n维特征映射到比n小的k维上,并最大程度降低其信息损失。其方法是从原始的空间顺序中找到一组相互正交的坐标轴,然后第一个新坐标轴的选择时原始数据中方差最大的方向,第二个是与第一个坐标轴正交的平面中方差最大的方向,以此类推。研究发现,大部分方差都包含在前k个坐标轴中,后面包含的很少,因此可以只报了前k个含有绝大部分方差的坐标轴,从而实现数据特征的降维。
通过计算数据矩阵的协方差矩阵,再计算协方差矩阵的特征值和特征向量,选取特征值最大(即方差最大)的k个特征所对应的特征向量组成新矩阵,就能实现上面的降维方法。
计算协方差矩阵特征值和特征向量有两种方法,因此PCA算法的实现也有两种:
基于特征值分解协方差矩阵
对于n维数据集X={x1,x2,...,xn}进行降维主要步骤如下所示:
- 零均值化(中心化):每一个特征减去各自的均值。(关于这一步的解释见链接)
- 计算协方差矩阵n1XXT。(推导过程可见链接)
- 用特征值分解法求协方差矩阵的特征和特征向量
特征值分解矩阵
若矩阵A是一个m×m的实对称矩阵(A=AT),矩阵A通过特征值分解可以化为下式:
A=QΣQ−1=QΣQT
其中Q是矩阵A特征向量组成的矩阵,Σ是一个对角阵,对角线上的元素为特征值,QQT=I。(对于正交矩阵 QT=Q−1)
上述式子的推导过程见链接
基于SVD(奇异值)分解矩阵
基于SVD的方法则是通过奇异值分解来求协方差矩阵的特征值和特征向量。特征值分解要求矩阵A必须为实对称矩阵,但遇到一般性矩阵(如m×n的矩阵A),则需要用SVD的方法进行分解。
对于矩阵A可以有以下分解形式:
A=UΣVT
其中,U和V均为单位正交矩阵,即UUT=I,VVT=I,Σ仅在主对角线上有值,称为奇异值。且U∈Rm×m,Σ∈Rm×n,V∈Rn×n。
推导过程见链接
局部线性嵌入(LLE)
PCA为线性降维方法,但现实中存在很多非线性高维数据,为了有效处理非线性数据,提出了LLE方法。
LLE基本原理
LLE方法基于假设:局部原始数据近似位于一张超平面上,局部内某一数据可以由其领域数据线性表示。数学表达为:
xi=wi1∗xi1+wi2∗xi2+...+wik∗xik
其中的xi表示原始数据集中第i个元素,xik表示x领域内的第k个数据,wik表示对应的权重。在xi确定的情况下,可以使用K-NN等算法求其领域数据。
降维后,样本在低维上的投影也应该满足其原有的线性关系,y是x在低维空间上的投影,则y应该满足:
yi=wi1∗yi1+wi2∗yi2+...+wik∗yik
LLE算法的基本步骤为:
- 在高维空间中根据样本的近邻样本求权重系数
- 在权重系数和关系不变的情况下计算样本低维投影
权重计算
对m个n维样本{x1,x2,...,xm},xj为xi的近邻样本,通过最小化损失函数(均方差)来求权重系数:
l(wi)=∥xi−j=1∑kwijxij∥2
对权重添加约束条件:∑j=1kwij=1
代入上式变为:
l(wi)=∥j=1∑kwijxi−j=1∑kwijxij∥2=∥j=1∑kwij(xi−xij)∥2(3)=∥[xi−xi1,...,xi−xik]Wi∥2(4)=WiTQiTQiWi
其中,Wi=[wi1,...,wik],Qi=[xi−xi1,...,xi−xik]。
关于公式中(3)→(4)的个人思考,损失函数是在计算均方差,之前说到方差是协方差的特殊情况而协方差又可以表示为n1XXT,因此(3)可以转化为(4)式。
令Ai=QiTQi,则可以得到:l(Wi)=WiTAiWi。
将权重的约束矩阵化为:∑j=1kwij=WiT1k=1,其中1k为k维的全1向量。
对于带约束的优化问题,通常用拉格朗日乘子法(Lagrange Multiplier),将约束式用一个系数与原式合并为一个式子(拉格朗日函数),从而消除约束,再对拉格朗日函数求导求极值极值验证得最优解。(具体见链接)
使用拉格朗日乘子法得到:
l(Wi)=WiTAiWi+λ(WiT1k−1)
对上式的W求偏导得:
∂Wi∂l=2AiWi+λ1kT
为求极值点,令偏导数为0,可得:Wi=−21λAi−11k。
因为 WiT1k=1,对Wi归一化后上式可以化为:
Wi=1kTZi−11kAi−11k
Wi为一个向量,若原始数据集中有m个数据,则可求得m个Wi,组成一个k×m的矩阵W:
W=⎣⎡Wi1...Wik..........Wm1...Wmk⎦⎤
求解低维数据
在求得Wi后,根据Wi可求低维数据,低维数据yi也应满足以下的关系:
yi=wi1∗yi1+wi2∗yi2+...+wik∗yik
同样,通过最小化损失函数(均方差)来求解,高维的式子中高维数据已知因此求W,低维则反过来在已知W的情况下求低维数据。
l(y)=i=1∑m∥yi−j=1∑kwijyij∥2=i=1∑m∥(yIi−ymi)∥2
其中,Ii表示从低维数据集y中取的第i个数据,mi则是由wik组成的稀疏矩阵。进一步化简得:
l(y)=i=1∑m∥y(Ii−mi)∥2=yRRTyT
其中,R=(Ii−mi)。
为了得到标准化的低维数据,添加两个约束:
m1i=1∑myiyiT=Idi=1∑myi=0
其中,Id为d维的单位矩阵。第一个约束表示低维数据的协方差矩阵之和为单位矩阵的m倍,第二个约束表示所有低维数据的和为0。
第一个约束条件可化为:
其中,y=[y1,y2,...,ym]。
同样使用拉格朗日乘子法得:
l(y)=yRRTyT+λ(yyT−nId)
对y求偏导,令偏导数为0得:
∂y∂l=2RRTyT+λyTRRTyT=−21λyT
令σ=−21λ,M=RRT,上式化为:
MyT=σyT
由上文的特征向量和特征值公式可得,yT为矩阵M的特征向量构成的矩阵。要得到最小d维数据集,只需求出矩阵M最小的d个特征向量组成的矩阵Y=(y1,y2,...,yd)T。
拉普拉斯特征映射(Laplacian Eigen-map, LE)
LE方法的基本思想和LLE类似,但区别在于其使用了拉普拉斯矩阵。
拉普拉斯矩阵
拉普拉斯矩阵L的定义为:L=D−W。其中D为度矩阵,W为邻接矩阵。
度矩阵和邻接矩阵
度矩阵和邻接矩阵的概念与图有关,对于图 G(V,E),,V=(v1,v2,...,vn)是图中所有点的集合,E是边的集合,wij是点vi和vj间的权重,没有边连接的两个点间权重为0。
对于图中任意一点vi,它的度di定义为和该点相连的所有边的权重和:
di=j=1∑nwij
根据这点,可以得到一个n×n的度矩阵D,为一个对角矩阵,如下所示:
⎣⎡d1⋯⋮⋯⋯d2⋮⋯⋯⋯⋱⋯⋯⋯⋮dn⎦⎤
此外,还可以得到图的n×n邻接矩阵W,第i行的第j个值表示对应wij,可以看出D和W都是对称矩阵。
拉普拉斯矩阵的性质
- 拉普拉斯矩阵是对称矩阵(因为D和W都是对称矩阵)
- 所有特征值都是实数。(对称矩阵的性质)
- 通过其定义易证明,对任意向量f有:
fTLf=21i,j=1∑nwij(fi−fj)2
- 为半正定矩阵,且有0=λ1≤λ2≤...λn,最小的特征值为0。
LE的思想
与LLE类似,LE首先在高维空间中描述样本结构。假设原始数据集为X=[x1,x2,...,xn],X∈Rm,为一个n×m的集合。
对于样本点xi,若存在点xj为其近邻则有:
Wij=exp∥xi−xj∥2/t
t为指定的某个常数,若xj不是近邻则Wij=0。(这里是使用K-NN算法构建邻接矩阵)
通过高维计算出W后,在低维空间中需要保持样本的结构,低维数据Y=[y1,y2,...,yn],Y∈Rk,为一个n×k的数据集。在低维空间中要让xi尽可能接近xj,则需要最小化目标函数:
mini,j∑∥yi−yj∥2Wij=i=1∑nj=1∑n(yiTyi−2yiTyj+yjTyj)Wij=2i=1∑nDiiyiTyi−2i=1∑nj=1∑nyiTyiWij
此处的Dii=∑j=1nWij,即图的度矩阵。令Y=∑i=1nyi,上式可继续化为:
2trace(YTDY)−2i=1∑nyiT(j=1∑njiWij)=2trace(YTDY)−2i=1∑nyiT(YW)i=2trace(YTDY)−2trace(TTWY)=2trace(YT(D−W)Y)
由拉普拉斯矩阵的定义L=D−W,可得最终转化的目标函数:
mintrace(YTLY)s.t.YTDY=I
YTDY=I的限制条件是为了消除低维空间中的缩放因子,并保证优化问题有解。
同样使用拉格朗日乘子法求解,其中Λ为一个对角矩阵:
f(Y)=trace(YTLY)+trace(Λ(YTDY−I))
对Y求偏导,用到了矩阵的迹求导:
∂Y∂f(Y)=LY+LTY+DTYΛT+DYΛ=2LY+2DYΛ=0
即:LY=−DYΛ,对于单个样本值y,式子可化为D−1Ly=λy,可以看出这变成了广义特征值分解问题,通过对D−1L进行特征值分解取其第二小到第m小(最小值为0,故舍弃)的特征值所对应的特征向量即为降维后的Y。