数据结构与算法总结 - 第一篇1. 10个最常用的数据结构数组链表栈队列散列表二叉树堆跳表图 Trie

1. 10个最常用的数据结构

数组
链表
栈
队列
散列表
二叉树
堆
跳表
图
Trie树

2. 10个最常用的算法

递归
排序
二分查找
搜索
哈希算法
贪心算法
分治算法
回溯算法
动态规划
字符串匹配算法

3. 数据结构和算法的关系

数据结构是数据的组织方式,为算法服务.
算法就是针对特定的数据结构执行操作.

4. 常见的时间复杂度

O(1)
O(logn)
O(n)
O(nlogn)
O的k次方
指数阶 O(2的n次方)
阶乘阶 O(n!)

5. 时间复杂度称为渐进时间复杂度,表示算法的执行时间随数据规模的增长关系.

6. 空间复杂度称为渐进空间复杂度,表示算法的存储空间随数据规模的增长关系.

7. 线性表

线性表是数据排成像一条线一样的结构.
每个线性表上的数据最多只有向前和向后两个方向.
数组,链表,队列,栈都是线性表.

8. 非线性表

非线性表中,数据之间不是简单的前后关系
二叉树,堆,图都是非线性表

9. 数组

数组是一种线性表数据结构,用一组连续的内存空间,存储一组具有相同类型的数据.
连续的内存空间和相同类型的数据
- 优点:让数组可以随机访问/根据下标随机访问数组元素.
- 缺点:数组中添加,删除元素,为了保证内存连续性,需要做大量的数据搬移.
数组的查找时间复杂度并不是O(1),即使是排序后的数组,查找某个数据,也需要O(logn)
容器/ArrayList和数组比较优点
- ArrayList将很多数组的操作进行封装,便于使用
- ArrayList支持动态扩容
  - 动态扩容依然免不了内存中数据搬移,如果能事先确定数据量,创建ArrayList时应先指定数据大小.
容器/ArrayList和数组比较缺点
- ArrayList无法存储基本类型,要存储基本类型,会涉及装箱,拆箱有性能损耗
- 数据量已知,且对数据的操作很简单,不涉及ArrayList大部分方法,可以使用数组
容器/ArrayList和数组如何选择
- 业务开发,直接使用ArrayList即可,简单.性能低一点几乎无影响
- 底层开发比较网路框架,性能要优化到极致,要使用数组.

10. 链表: 通过指针将一组零散的内存块串联在一起.

单链表

Node head = node0;
Node tail = noden;
head.next = node1;
**
tail.next = null;

循环链表

Node head = node0;
Node tail = noden;
head.next = node1;
**
tail.next = head;

双向链表

Node head = node0;
Node tail = noden;
head.next = node1;
head.pre = null;
**
tail.next = null;
tail.pre = noden-1;

双向循环链表

Node head = node0;
Node tail = noden;
head.next = node1;
head.pre = tail;
**
tail.next = head;
tail.pre = noden-1;

11. 数组和链表的比较

链表插入,删除的时间复杂度是O(1),随机访问的时间复杂度是O(n).
数组插入,删除的时间复杂度是O(n),随机访问的时间复杂度是O(1).
数组使用内存上的连续空间,对CPU缓存友好,链表中数据在内存上不连续,对CPU缓存不友好.
数组缺点是大小固定,声明后就占用完整空间,声明数组过大,会浪费内存,甚至会直接OOM,声明过小后面数组扩容会影响性能.
链表天然支持动态扩容.但链表中每个元素都要存储next及pre指针,单个元素占用内存更大.
如果数据个数可控,使用数组性能更好.避免存储next及pre指针占用额外空间.

12. 链表的几个问题

1. 单链表实现LRU

public class LRULinkedList<T>{
    class Node<T>{
        public T data;
        public Node next;
        public Node(T data, Node next){
            super();
            this.data = data;
            this.next = next;
        }
    }
    
    private static int DEFAULT_CAPACITY = 6;
    private int capacity = DEFAULT_CAPACITY;
    private int count = 0;
    private Node head = null;
    public LRULinkedList(int capacity){
        this.capacity = capacity;
    }
    public boolean isFull(){
        return count == capacity;
    }
    public Node createNode(T data){
       Node node = new Node(data, null);
       return node;
    }
    public void access(T data){
        if(data == null){
            throw new IllegalArgumentException("访问的元素不能为空!");
        }
        if(head == null){
            head = createNode(data);
            count++;
            return;
        }
        if(head.data.equals(data)){
            //头结点就是要访问的数据
            return;
        }
        Node curr = head;
        while(curr.next != null && !curr.next.data.equals(data)){
            curr = curr.next;
        }
        if(curr.next != null && curr.next.data.equals(data)){
            //要访问的元素已存在
            Node target = curr.next;
            curr.next = target.next;
            target.next = head;
            head = target;
        }else{
            //要访问的元素不存在
            if(isFull()){
                //链表已满
            	//删除当前尾结点
            	
            	//这样写有问题,打印结果:
            	//当前数据为:  -> 10 -> 8 -> 6 -> 4 -> 2 -> 9 -> 7 -> 5 -> 3 -> 1
//                Node c = head;
//                while(c != null && c.next != null) {
//                	c = c.next;
//                }
//                c = null;
                
            	Node c = head;
				while(c != null && c.next != null && c.next.next != null) {
					c = c.next;
				}
				c.next = null;
            	
                addHead(data);
            }else{
                //链表未满
                //直接添加头结点
            	addHead(data);
                count++;
            }
        }
    }
    private void addHead(T data) {
    	Node target = createNode(data);
        target.next = head;
        head = target;
    }
    private void printAll() {
        System.out.print("当前数据为: ");
        Node curr = head;
        while(curr != null) {
            System.out.print(" -> " + curr.data);
            curr = curr.next;
        }
    }
    public static void main(String[] args) {
        LRULinkedList<Integer> list = new LRULinkedList<>(6);
        list.access(1);
        list.access(3);
        list.access(5);
        list.access(7);
        list.access(9);
        list.access(2);
        list.access(4);
        list.access(6);
        list.access(8);
        list.access(10);
        list.printAll();
    	
    	Person a = new Person();
    	a.name = "a";
    	Person b = new Person();
    	b.name = "b";
    	Person c = new Person();
    	c.name = "c";
    	a.friend = b;
    	b.friend = c;
    	
    	//这样写有问题: b的朋友:name:c
//    	try {
//    		c = null;
//    		System.out.println("b的朋友:" + b.friend);
//		} catch (Exception e) {
//		}
    	
//    	try {
//    		b.friend = null;
//    		System.out.println("b的朋友:" + b.friend);
//		} catch (Exception e) {
//		}
    }
    public static class Person{
    	public String name;
    	public Person friend;
    	@Override
    	public String toString() {
    		return "name:" + name;
    	}
    }
}

2. 上面的例子引出1个认识误区

//A.attr和C都指向同一个对象B
A.attr = B;
BInstance C = B;
//C置空
C = null;
//此时A.attr并不是null

A.attr -> B
C -> B
C = null, 仅仅是断开了C这个变量名和 B这个实例的链接,但是B依然被 A.attr 继续链接. B本身不会被置空.

3. 约瑟夫问题一道阿里笔试题：我是如何用一行代码解决约瑟夫环问题的

3.1. 使用数组解决

/**
 * 约瑟夫问题 : 使用数组解决
 */
public class JosephusArray {
    public static void main(String[] args) {
        JosephusArray t = new JosephusArray();
        int[] arr = new int[11];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = i + 1;
        }
        System.out.println("数组的值:");
        Arrays.stream(arr).forEach(System.out::println);
        int result = t.findLastItemData(arr, 3);
        System.out.println("最终剩余Item的值:" + result);
    }

    public int findLastItemData(int[] arr, int k) {
        if (arr == null || arr.length <= 0) {
            return -1;
        }
        if (arr.length == 1) {
            return 0;
        }
        int length = arr.length;
        int count = arr.length;
        int index = 0;
        int step = 0;
        int tagIndex = -1;
        while (count > 1) {
            while (step < k) {
                if (arr[index] != -1) {
                    step++;
                    tagIndex = index;
                }
                if (index == length - 1) {
                    index = 0;
                } else {
                    index++;
                }
            }
            arr[tagIndex] = -1;
            step = 0;
            count--;
        }
        while(arr[index] == -1) {
            if (index == length - 1) {
                index = 0;
            } else {
                index++;
            }
        }
        return arr[index];
    }
}

//打印结果:
数组的值:
1
2
3
4
5
6
7
8
9
10
11
最终剩余Item的值:7

3.2. 使用循环列表解决

public class JosephusLinkedList<T> {
	public static class Node<T>{
		public T data;
		public Node<T> next;
		public Node(T data) {
			super();
			this.data = data;
		}
	}
	private Node<T> head;
	private Node<T> tail;
	public void add(Node<T> node) {
		if(head == null) {
			head = tail = node;
			head.next = head;
		}else {
			tail.next = node;
			node.next = head;
			tail = node;
		}
	}
	public void remove(Node<T> node) {
		if(head == null || node == null) {
			return;
		}
		Node curr = head;
		while(curr.next != node) {
			curr = curr.next;
		}
		if(head.next == head) {
			head.next = null;
			head = tail = null;
			return;
		}
		Node next = node.next;
		curr.next = next;
		if(node == head) {
			head = next;
		}
		node.next = null;
	}
	public int findLastItemData(int k) {
		if(head == null) {
			return -1;
		}
		Node curr = head;
		Node pre = null;
		int step = 0;
		while(head.next != head) {
			while(step < k) {
				pre = curr;
				curr = curr.next;
				step++;
			}
			remove(pre);
			step = 0;
		}
		return (int) head.data;
	}
	public static void main(String[] args) {
		JosephusLinkedList<Integer> t = new JosephusLinkedList<Integer>();
		for(int i=1;i<=11;i++) {
			t.add(new Node<Integer>(i));
		}
		int result = t.findLastItemData(5);
		System.out.println("最后剩余项的值:" + result);
	}
}

//打印结果:
最后剩余项的值:8

4. 数组实现LRU

public class LRUBasedArray<T> {
	public static int DEFAULT_CAPACITY = 6;
	private int capacity = DEFAULT_CAPACITY;
	private T[] data;
	private int count;
	private Map<T, Integer> positionHolder;
	
	public LRUBasedArray(int capacity) {
		this.count = 0;
		this.capacity = capacity;
		this.data = (T[]) new Object[capacity];
		this.positionHolder = new HashMap<>(capacity);
	}
	public void clear() {
		positionHolder.clear();
		data = (T[]) new Object[capacity];
		count = 0;
	}
	public boolean isFull() {
		return count == capacity;
	}
	public boolean contains(T item) {
		return positionHolder.containsKey(item);
	}
	public void access(T item) {
		//首先判断item是否已存在
		boolean contains = contains(item);
		if(contains) {
			//获取item所在索引
			int index = positionHolder.get(item);
			if(index == 0) {
				//当前要访问的数据,已经在数组头部
				return;
			}else {
				//当前要访问的数据,不在数组头部,需要将数据移到头部,并将其他数组元素右移
				transferToRight(index);
				setHead(item);
			}
		}else {
			//判断数组是否已满
			boolean isFull = isFull();
			if(isFull) {
				//数组已满
				//将尾元素置空
				removeTail();
				//将元素右移
				transferToRight(capacity - 1);
				//插入头元素
				setHead(item);
			}else {
				//数组未满
				//将元素右移
				transferToRight(count);
				//插入头元素
				setHead(item);
				//count加一
				count++;
			}
		}
	}
	public void setHead(T item) {
		data[0] = item;
		positionHolder.put(item, 0);
	}
	public void removeTail() {
		positionHolder.remove(data[capacity - 1]);
		data[capacity - 1] = null;
	}
	public void transferToRight(int toIndex) {
		for(int i = toIndex-1; i >= 0; i--) {
			data[i + 1] = data[i];
			positionHolder.put(data[i + 1], i+1);
		}
	}
	public void printAll() {
		for(int i = 0; i < count; i++) {
			System.out.println("item"+i+" : " + data[i]);
		}
	}
	public static void main(String[] args) {
		LRUBasedArray<Integer> lruBasedArray = new LRUBasedArray<>(6);
		lruBasedArray.access(1);
		lruBasedArray.access(2);
		lruBasedArray.access(3);
		lruBasedArray.access(4);
		lruBasedArray.access(5);
		lruBasedArray.access(6);
		lruBasedArray.access(7);
		lruBasedArray.access(3);
		lruBasedArray.access(3);
		lruBasedArray.access(3);
		lruBasedArray.access(8);
		lruBasedArray.access(9);
		lruBasedArray.access(10);
		lruBasedArray.printAll();
	}
}

//运行结果
item0 : 10
item1 : 9
item2 : 8
item3 : 3
item4 : 7
item5 : 6

5. 自定义单链表,校验字符是否是回文字符串

public class PalindromeSinglyList<T> {
	public class Node<T>{
		public T data;
		public Node<T> next;
		public Node(T data, Node<T> next) {
			super();
			this.data = data;
			this.next = next;
		}
		@Override
		public String toString() {
			return "Node [data=" + data + "]";
		}
	}
	
	public Node<T> head;
	public void add(T item) {
		if(head == null) {
			head = new Node<T>(item, null);
			return;
		}
		Node<T> tail = head;
		while(tail.next != null) {
			tail = tail.next;
		}
		tail.next = new Node<T>(item, null);
	}
	public Node inverseList(Node tail) {
		Node curr = head;
		Node next = null;
		while(curr.next != tail) {
			next = curr.next.next;
			curr.next.next = head;
			head = curr.next;
			curr.next = next;
		}
		tail.next = head;
		curr.next = null;
		head = tail;
		return tail;
	}
	public boolean compareTwoList(Node leftHead, Node rightHead) {
		if(leftHead == null || rightHead == null) {
			return false;
		}
		while(leftHead != null && rightHead != null && leftHead.data.equals(rightHead.data)) {
			leftHead = leftHead.next;
			rightHead = rightHead.next;
		}
		return leftHead == null && rightHead == null;
	}
	private void printNode(Node node) {
		while(node != null) {
			System.out.println(node);
			node = node.next;
		}
	}
	public boolean isPalindrome() {
		if(head == null) {
			//空列表
			return false;
		}
		if(head.next == null) {
			//只有头元素
			return true;
		}
		if(head.next.next == null) {
			//只有2个元素
			return head.data.equals(head.next.data);
		}
		//有>=3个元素
		//首先判断元素个数是奇数还是偶数
		Node slow = head;
		Node fast = head;
		while(slow.next != null && fast.next != null && fast.next.next != null) {
			slow = slow.next;
			fast = fast.next.next;
		}
		Node leftHead,rightHead;
		if(fast.next != null) {
			//偶数个元素
			rightHead = slow.next;
			leftHead = inverseList(slow);
		}else {
			//奇数个元素
			rightHead = slow;
			leftHead = inverseList(slow);
		}
		//打印两个Node及后续Node
		System.out.println("左半边列表元素:");
		printNode(leftHead);
		System.out.println("右半边列表元素:");
		printNode(rightHead);
		boolean result = compareTwoList(leftHead, rightHead);
		System.out.println("是否回文字符串:" + result);
		return result;
	}
	public static void main(String[] args) {
		int[] d1 = new int[] {1,2,3,4,3,2,1};
		int[] d2 = new int[] {1,2,3,2,1};
		int[] d3 = new int[] {1,2,2,1};
		int[] d4 = new int[] {1,0,1,0};
		PalindromeSinglyList list1 = new PalindromeSinglyList();
		for(int item:d1) {
			list1.add(item);
		}
		PalindromeSinglyList list2 = new PalindromeSinglyList();
		for(int item:d2) {
			list2.add(item);
		}
		PalindromeSinglyList list3 = new PalindromeSinglyList();
		for(int item:d3) {
			list3.add(item);
		}
		PalindromeSinglyList list4 = new PalindromeSinglyList();
		for(int item:d4) {
			list4.add(item);
		}
		list1.isPalindrome();
		System.out.println("===============");
		list2.isPalindrome();
		System.out.println("===============");
		list3.isPalindrome();
		System.out.println("===============");
		list4.isPalindrome();
	}
}

//运行结果
左半边列表元素:
Node [data=4]
Node [data=3]
Node [data=2]
Node [data=1]
右半边列表元素:
Node [data=4]
Node [data=3]
Node [data=2]
Node [data=1]
是否回文字符串:true
===============
左半边列表元素:
Node [data=3]
Node [data=2]
Node [data=1]
右半边列表元素:
Node [data=3]
Node [data=2]
Node [data=1]
是否回文字符串:true
===============
左半边列表元素:
Node [data=2]
Node [data=1]
右半边列表元素:
Node [data=2]
Node [data=1]
是否回文字符串:true
===============
左半边列表元素:
Node [data=0]
Node [data=1]
右半边列表元素:
Node [data=1]
Node [data=0]
是否回文字符串:false

6. 单链表反转

public class LinkedListTest {
    public class Node<T>{
        public T data;
        public Node<T> next;
        public Node(T data){
            this.data = data;
        }
    }
    public Node reverse(Node list) {
        if(list == null) {
            throw new IllegalArgumentException("链表头结点不能为空!");
        }
        if(list.next == null) {
            return list;
        }
        Node curr = list;
        Node next = null;
        while(curr.next != null) {
            next = curr.next.next;
            curr.next.next = list;
            list = curr.next;
            curr.next = next;
        }
        return list;
    }
    private void testReverse() {
        Node list = new Node<Integer>(3);
        Node n1 = new Node<Integer>(2);
        Node n2 = new Node<Integer>(4);
        Node n3 = new Node<Integer>(6);
        Node n4 = new Node<Integer>(8);
        list.next = n1;
        n1.next = n2;
        n2.next = n3;
        n3.next = n4;
        Node result = reverse(list);
        while(result != null) {
                System.out.println("当前值:" + result.data);
                result = result.next;
        }
    }
    public static void main(String[] args) {
        LinkedListTest t = new LinkedListTest();
        t.testReverse();
    }
}

//运行结果:
当前值:8
当前值:6
当前值:4
当前值:2
当前值:3

单链表中环的检测

public boolean checkCircle(Node list) {
    if (list == null || list.next == null || list.next.next == null) {
        return false;
    }
    Node slow = list;
    Node fast = list;
    while(slow.next != null && fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
        if(slow == fast) {
            return true;
        }
    }
    return false;
}
private void testCheckCircle() {
    Node list = new Node<Integer>(3);
    Node n1 = new Node<Integer>(2);
    Node n2 = new Node<Integer>(4);
    Node n3 = new Node<Integer>(6);
    Node n4 = new Node<Integer>(8);
    list.next = n1;
    n1.next = n2;
    n2.next = n3;
    n3.next = n1;
//		n3.next = n4;
    boolean result = checkCircle(list);
    System.out.println("当前单链表有环:" + result);
}

public static void main(String[] args) {
    LinkedListTest t = new LinkedListTest();
    t.testCheckCircle();
}

//运行结果:
当前单链表有环:true

7. 两个有序单链表的合并

public Node mergeTwoSortedList(Node l1, Node l2) {
    if(l1 == null || l2 == null) {
        throw new IllegalArgumentException("参数不能为空!");
    }
    Node soldier = new Node(null);
    Node curr = soldier;
    while(l1 != null && l2 != null) {
        if(l1.data.hashCode() < l2.data.hashCode()) {
            curr.next = l1;
            l1 = l1.next;
        }else {
            curr.next = l2;
            l2 = l2.next;
        }
        curr = curr.next;
    }
    if(l1 != null) {
        curr.next = l1;
    }
    if(l2 != null) {
        curr.next = l2;
    }
    return soldier.next;
}
public void testMergeTwoSortedList() {
    Node<Integer> l1 = new Node<Integer>(1);
    Node<Integer> l11 = new Node<Integer>(3);
    Node<Integer> l12 = new Node<Integer>(9);
    Node<Integer> l13 = new Node<Integer>(19);
    l1.next = l11;
    l11.next = l12;
    l12.next = l13;

    Node<Integer> l2 = new Node<Integer>(2);
    Node<Integer> l21 = new Node<Integer>(4);
    Node<Integer> l22 = new Node<Integer>(6);
    Node<Integer> l23 = new Node<Integer>(12);
    l2.next = l21;
    l21.next = l22;
    l22.next = l23;
    Node result = mergeTwoSortedList(l1, l2);
    while (result != null) {
        System.out.println("当前项值:" + result.data);
        result = result.next;
    }
}

public static void main(String[] args) {
    LinkedListTest t = new LinkedListTest();
    t.testMergeTwoSortedList();
}

//运行结果:
当前项值:1
当前项值:2
当前项值:3
当前项值:4
当前项值:6
当前项值:9
当前项值:12
当前项值:19

8. 删除单链表倒数第K个结点

public Node deleteLastK(Node list, int k) {
    if(list == null || k < 1) {
        throw new IllegalArgumentException("参数有误!");
    }
    Node fast = list;
    int count = 0;
    while(fast.next != null && count < k - 1) {
        fast = fast.next;
        count++;
    }
    if(count < k - 1) {
        throw new IllegalArgumentException("列表长度不够!");
    }
    if(fast.next == null) {
        //说明链表中只有k个结点,只能删除头节点
        Node curr = list;
        list = list.next;
        curr.next = null;
        return curr;
    }
    Node slow = list;
    fast = fast.next;
    while(slow.next != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next;
    }
    Node next = slow.next.next;
    slow.next.next = null;
    slow.next = next;
    return list;
}
public void testDeleteLastK() {
    Node list = new Node<Integer>(3);
    Node n1 = new Node<Integer>(2);
    Node n2 = new Node<Integer>(4);
    Node n3 = new Node<Integer>(6);
    Node n4 = new Node<Integer>(8);
    Node n5 = new Node<Integer>(10);
    Node n6 = new Node<Integer>(12);
    list.next = n1;
    n1.next = n2;
    n2.next = n3;
    n3.next = n4;
    n4.next = n5;
    n5.next = n6;
    Node result = deleteLastK(list,4);
    while(result != null) {
        System.out.println("当前项值:" + result.data);
        result = result.next;
    }
}
public static void main(String[] args) {
    LinkedListTest t = new LinkedListTest();
    t.testDeleteLastK();
}

//运行结果:
当前项值:3
当前项值:2
当前项值:4
当前项值:8
当前项值:10
当前项值:12

9. 求单链表的中间节点

public Node findMiddleNode(Node list) {
    if(list == null) {
        throw new IllegalArgumentException("参数不能为空!");
    }
    if(list.next == null || list.next.next == null) {
        //仅有1个节点,或仅有2个节点. 以头节点作为中间节点
        return list;
    }
    Node slow = list;
    Node fast = list;
    while(slow.next != null && fast.next != null && fast.next.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow;
}
public void testFindMiddleNode() {
    Node list = new Node<Integer>(3);
    Node n1 = new Node<Integer>(2);
    Node n2 = new Node<Integer>(4);
    Node n3 = new Node<Integer>(6);
    Node n4 = new Node<Integer>(8);
    Node n5 = new Node<Integer>(10);
    Node n6 = new Node<Integer>(12);
    list.next = n1;
    n1.next = n2;
    n2.next = n3;
    n3.next = n4;
    n4.next = n5;
    n5.next = n6;
    Node middle = findMiddleNode(list);
    System.out.println("中间节点的值:" + middle.data);
}
public static void main(String[] args) {
    LinkedListTest t = new LinkedListTest();
    t.testFindMiddleNode();
}

//运行结果:
中间节点的值:6

13. 栈 : 一种操作受限的线性表结构,仅支持单方向的入栈及出栈.

1. 用2个栈来实现浏览器的前进及回退

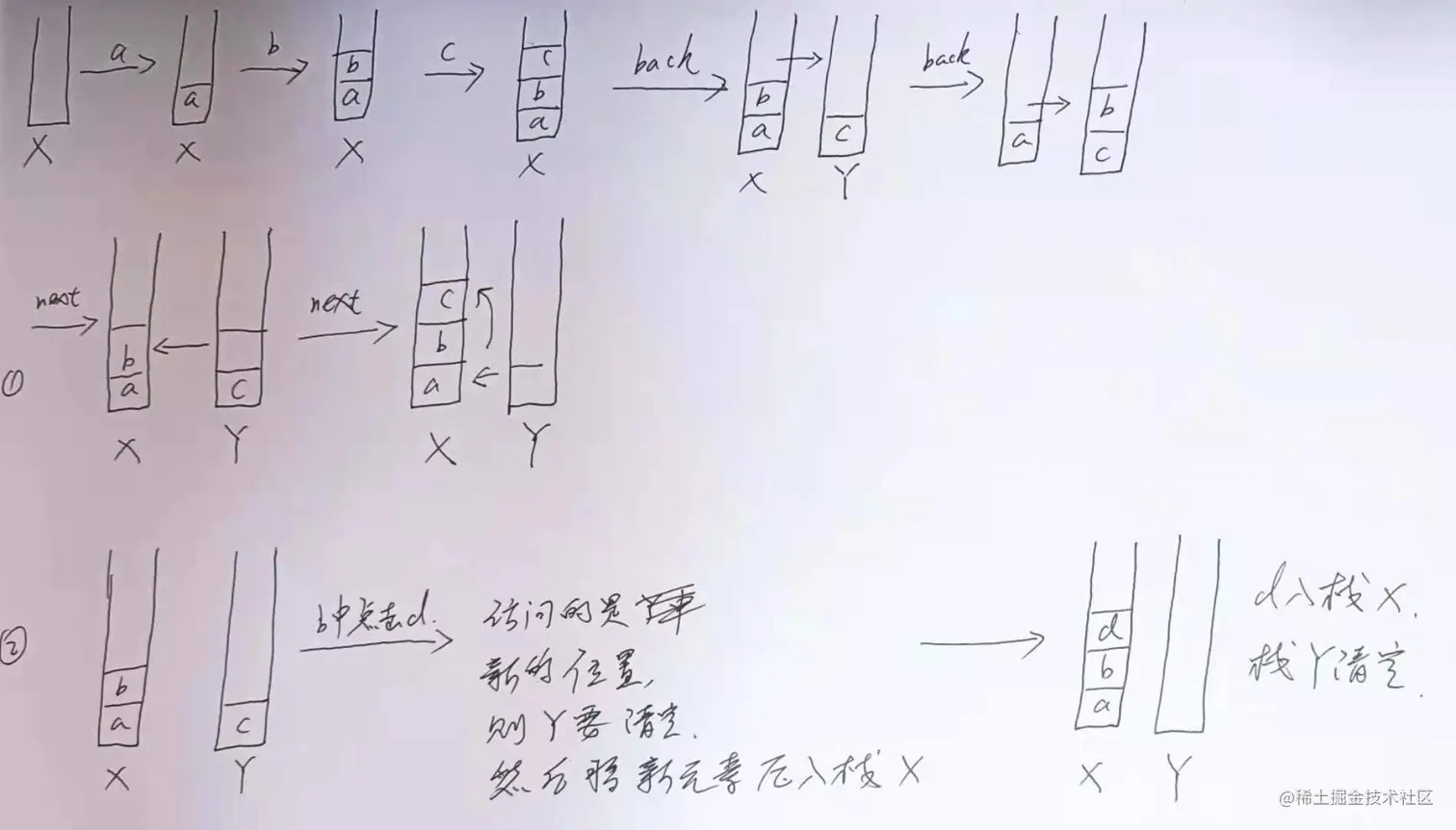
用2个栈实现浏览器的前进及回退功能.jpg

2. 使用链表实现栈

public class StackBasedOnLinkedList {
    public class Node {
        public int data;
        public Node next;
        public Node(int data, Node next) {
            super();
            this.data = data;
            this.next = next;
        }
        public int getData() {
            return data;
        }
    }

    private Node top;
    public void push(int data) {
        Node node = new Node(data, null);
        if (top == null) {
            top = node;
        } else {
            node.next = top;
            top = node;
        }
    }
    public int pop() {
        if(top == null) {
            return -1;
        }
        int value = top.data;
        top = top.next;
        return value;
    }
    public void printAll() {
        while(top!=null) {
            System.out.println("当前值:" + top.data);
            top = top.next;
        }
    }
    public static void main(String[] args) {
        StackBasedOnLinkedList t = new StackBasedOnLinkedList();
        t.push(1);
        t.push(2);
        t.push(3);
        t.push(4);
        t.push(5);
        t.printAll();
    }
}

//运行结果:
当前值:5
当前值:4
当前值:3
当前值:2
当前值:1

3.使用2个栈来实现浏览器的打开,前进,后退功能

public class SimpleBrowser {
    public class Node {
        public String data;
        public Node next;

        public Node(String data, Node next) {
            super();
            this.data = data;
            this.next = next;
        }

        public String getData() {
            return data;
        }
    }

    public class StackBasedOnLinkedList {
        public Node top;

        public void push(Node node) {
            if (top == null) {
                top = node;
            } else {
                node.next = top;
                top = node;
            }
        }

        public String pop() {
            if (top == null) {
                return "当前栈为空!";
            }
            String result = top.data;
            top = top.next;
            return result;
        }

        public void clear() {
            while (top != null) {
                pop();
            }
        }

        public boolean hasElements() {
            return top != null;
        }
        public void printAll() {
            Node curr = top;
            while(curr != null) {
                System.out.println("当下元素值:" + curr.data);
                curr = curr.next;
            }
        }
    }

    public String currentPage;
    public StackBasedOnLinkedList backStack;
    public StackBasedOnLinkedList forwardStack;

    public SimpleBrowser() {
        this.backStack = new StackBasedOnLinkedList();
        this.forwardStack = new StackBasedOnLinkedList();
    }

    public boolean canGoBack() {
        return this.backStack.hasElements();
    }

    public boolean canGoForward() {
        return this.forwardStack.hasElements();
    }

    public String goBack() {
        if (canGoBack()) {
            String url = this.backStack.pop();
            this.forwardStack.push(new Node(url, null));
            this.currentPage = this.backStack.top == null ? null : this.backStack.top.data;
            return url;
        }
        return null;
    }

    public String goForward() {
        if (canGoForward()) {
            String url = this.forwardStack.pop();
            this.backStack.push(new Node(url, null));
            this.currentPage = url;
            return url;
        }
        return null;
    }

    public String open(String url) {
        this.forwardStack.clear();
        this.backStack.push(new Node(url, null));
        this.currentPage = url;
        return url;
    }

    public static void main(String[] args) {
        SimpleBrowser t = new SimpleBrowser();
        t.open("url1");
        t.open("url2");
        t.open("url3");
        t.open("url4");
        t.open("url5");
        t.open("url6");
        t.open("url7");
        t.open("url8");
        t.goBack();
        t.goBack();
        t.goBack();
        t.goBack();
        System.out.println("当前页面:" + t.currentPage);
        t.goBack();
        t.goForward();
        t.goForward();
        System.out.println("当前页面:" + t.currentPage);
        t.open("urlX");
        System.out.println("当前页面:" + t.currentPage);
    }
}

//运行结果
当前页面:url4
当前页面:url5
当前页面:urlX

14. 队列: 一种操作受限的线性表,先进先出,就是典型的队列.

1. 入队: 向队列尾部添加1个元素

2. 出队: 从队列头部取1个元素

3. 构建以数组为基础的队列

/**
 * 以数组构建的队列.
 */
public class QueueBasedOnArray {
    public String[] items;
    public int head, tail;
    public int size;

    public QueueBasedOnArray(int capacity) {
        this.size = capacity;
        this.items = new String[size];
        head = tail = 0;
    }

    /**
     * 判断队列是否为空
     * 
     * @return
     */
    public boolean isEmpty() {
        return head == tail;
    }

    /**
     * 判断队列是否已满
     * 
     * @return
     */
    public boolean isFull() {
        return tail == size;
    }

    /**
     * 入队
     * 
     * @param item
     * @return
     */
    public boolean enqueue(String item) {
        //只要队列之前满过,就不能继续添加元素,即使删除了元素
        if (isFull()) {
            // 当前队列已满
            return false;
        }
        items[tail] = item;
        tail++;
        return true;
    }

    /**
     * 出队
     * 
     * @return
     */
    public String dequeue() {
        if(isEmpty()) {
            return null;
        }
        String result = items[head];
        head++;
        return result;
    }

    /**
     * 打印当前队列中所有元素
     */
    public void printAll() {
        if (isEmpty()) {
            return;
        }
        System.out.println("队列所有元素:");
        for (int i = head; i < tail; i++) {
            System.out.println("当下元素值:" + items[i]);
        }
    }
    public static void main(String[] args) {
        QueueBasedOnArray t = new QueueBasedOnArray(6);
        t.enqueue("1");
        t.enqueue("2");
        t.enqueue("3");
        t.enqueue("4");
        t.enqueue("5");
        t.enqueue("6");
        t.enqueue("7");
        t.printAll();
        t.dequeue();
        t.dequeue();
        t.dequeue();
        t.dequeue();
        t.enqueue("X");
        t.printAll();
    }
}

//运行结果:
队列所有元素:
当下元素值:1
当下元素值:2
当下元素值:3
当下元素值:4
当下元素值:5
当下元素值:6
队列所有元素:
当下元素值:5
当下元素值:6

4. 构建以数组为基础的队列,只要数组有剩余空间,就可以继续添加元素

public class DynamicQueueBasedOnArray {
    public String[] items;
    public int head, tail;
    public int size;

    public DynamicQueueBasedOnArray(int capacity) {
        size = capacity;
        items = new String[size];
        head = tail = 0;
    }

    public boolean isEmpty() {
        return head == tail;
    }

    public String dequeue() {
        if (isEmpty()) {
                return null;
        }
        String result = items[head];
        head++;
        return result;
    }

    /**
     * 入队
     * 入队时候,如果队列尾部已经达到阈值,看头部是不是在0的位置,不在0的位置,说明队列从0->head-1的位置的元素已经被取出,队列仍然有空间.
     * 应该执行元素搬移,然后将新元素添加到队列尾部.
     * @param item
     * @return
     */
    public boolean enqueue(String item) {
        if (tail == size) {
            if (head == 0) {
                // 队列已满
                return false;
            } else {
                // 队列未满
                // 从0到head-1的位置都是空的
                for (int i = head; i < tail; i++) {
                    items[i - head] = items[i];
                }
                tail = tail - head;
                head = 0;
            }
        }
        items[tail] = item;
        tail++;
        return true;
    }

    public void printAll() {
        if (isEmpty()) {
            return;
        }
        System.out.println("当下队列所有元素:");
        for (int i = head; i < tail; i++) {
            System.out.println("当下元素值:" + items[i]);
        }
    }

    public static void main(String[] args) {
        DynamicQueueBasedOnArray t = new DynamicQueueBasedOnArray(6);
        t.enqueue("1");
        t.enqueue("2");
        t.enqueue("3");
        t.enqueue("4");
        t.enqueue("5");
        t.enqueue("6");
        t.enqueue("7");
        t.enqueue("8");
        t.printAll();
        t.dequeue();
        t.dequeue();
        t.dequeue();
        t.dequeue();
        t.enqueue("X");
        t.printAll();
    }
}

//运行结果:
当下队列所有元素:
当下元素值:1
当下元素值:2
当下元素值:3
当下元素值:4
当下元素值:5
当下元素值:6
当下队列所有元素:
当下元素值:5
当下元素值:6
当下元素值:X

5. 构建以链表为基础的队列,无界队列

/**
 * 以链表为基础构建队列
 * 链表本身是无界的,所以队列中元素数量不限制
 */
public class QueueBasedOnLinkedList {
    public class Node{
        public String data;
        public Node next;
        public Node(String data, Node next) {
            this.data = data;
            this.next = next;
        }
        public Node(String data) {
            this.data = data;
        }
    }

    public Node head;
    public Node tail;

    public void enqueue(String data) {
        if(head == null) {
            head = tail = new Node(data);
        }else {
            tail.next = new Node(data);
            tail = tail.next;
        }
    }
    public String dequeue() {
        if(head == null) {
            return null;
        }
        String data = head.data;
        head = head.next;
        if(head == null) {
            tail = null;
        }
        return data;
    }
    public void printAll() {
        Node curr = head;
        System.out.println("当下队列所有元素:");
        while(curr != null) {
            System.out.println("当下元素值:" + curr.data);
            curr = curr.next;
        }
    }
    public static void main(String[] args) {
        QueueBasedOnLinkedList t = new QueueBasedOnLinkedList();
        t.enqueue("1");
        t.enqueue("2");
        t.enqueue("3");
        t.enqueue("4");
        t.dequeue();
        t.printAll();
    }
}

//运行结果:
当下队列所有元素:
当下元素值:2
当下元素值:3
当下元素值:4

6. 构建以数组为基础的循环队列

tail指向的是一个当下还未存储元素的索引. 这样便于判断队列是否为空. tail指向的是'下一个',这样当 head==tail, 就说明队列是空的.
如果tail指向的是队列中最后一个元素,要判断队列是否为空,就要判断head位置或tail位置的元素是否是空. 为了保证是空,就要在每次出队时候将对应位置的数组元素置空,然后才能'head+1'.
1和2比较可见,tail指向'下一个'可以简化代码.
在以数组为基础构建的循环队列里,一定存在1个位置是要被浪费的.
- 因为tail指向'下一个',是当前没有存储元素的位置.
- 而循环队列是环形的,这个位置只能是环上的一个索引值.
- 不像数组构建的非循环对列,tail最大可以是n, 而n并不在数组索引值的范围.

public class CircleQueueBasedOnArray {
    public String[] items;
    public int head, tail;
    public int size;

    public CircleQueueBasedOnArray(int capacity) {
        head = tail = 0;
        size = capacity;
        items = new String[size];
    }

    public boolean isEmpty() {
        return head == tail;
    }

    public boolean isFull() {
        return (tail + 1) % size == head;
    }

    public boolean enqueue(String item) {
        if (isFull()) {
            return false;
        }
        items[tail] = item;
        tail = (tail + 1) % size;
        return true;
    }

    public String dequeue() {
        if (isEmpty()) {
            return null;
        }
        String result = items[head];
        head = (head + 1) % size;
        return result;
    }

    public void printAll() {
        if (isEmpty()) {
            return;
        }
        System.out.println("当前队列所有元素:");
        for (int i = head; i != tail; i = (i + 1) % size) {
            System.out.println("当下元素值:" + items[i]);
        }
    }
    public static void main(String[] args) {
        CircleQueueBasedOnArray t = new CircleQueueBasedOnArray(6);
        t.enqueue("1");
        t.enqueue("2");
        t.enqueue("3");
        t.enqueue("4");
        t.enqueue("5");
        t.enqueue("6");
        t.printAll();
        t.dequeue();
        t.dequeue();
        t.dequeue();
        t.printAll();
        t.enqueue("11");
        t.enqueue("12");
        t.enqueue("13");
        t.enqueue("14");
        t.enqueue("15");
        t.printAll();
    }
}

//当前运行结果:
//从打印结果可以看出: 以数组为基础构建的循环队列,会有1个位置被浪费掉,为了tail指向'下一个'.
当前队列所有元素:
当下元素值:1
当下元素值:2
当下元素值:3
当下元素值:4
当下元素值:5
当前队列所有元素:
当下元素值:4
当下元素值:5
当前队列所有元素:
当下元素值:4
当下元素值:5
当下元素值:11
当下元素值:12
当下元素值:13

15. 递归

1. 可以用递归解决的问题需满足的条件

1个问题的解可以分解为几个子问题的解.
原问题和子问题,除了数据规模不同,求解方法完全一致.
问题分解为子问题,不能无限分解,要有终止条件,即存在递归终止条件.

2. 递归的缺点

递归层级太深,会导致堆栈溢出.
- 以JVM为例,每个线程栈的深度是有限的,如果递归数量过大,不断将栈帧压入函数调用栈,超过限制就触发Stack Overfllow
递归可能存在重复计算问题
- 比如f(n) = f(n-1) + f(n-2), f(n-1) = f(n-2) + f(n-3) ,f(n-2)就被重复计算了2遍
- 为例避免重复计算,应该将之前指定参数的结果用散列表存下来
每一次调用递归,都会创建1个栈帧压栈,栈帧中包含临时变量,多次调用会增加算法的空间复杂度.
- 相对于while循环,我们可以声明1个变量,在while循环中反复使用,空间复杂度低
递归是'同步'的,需等待之前的调用结果,如果调用次数过大,会积累至很高的时间成本.

3. 几个递归问题

3.1. n阶楼梯,每次可以上1阶或者上2阶,一共有多少种走法?

private Map<Integer,Integer> results = new HashMap<Integer,Integer>();
public int goStairs(int n){
    if(n <= 1){
        return 1;
    }
    if(n == 2){
        return 2;
    }
    if(results.containsKey(n)){
        return results.get(n);
    }
    return goStairs(n - 1) + goStairs(n - 2);
}

16. 如何评价1个排序算法: 从排序算法的执行效率, 排序算法的空间复杂度, 排序算法的稳定性 3个方面来衡量.

1. 排序算法的执行效率

最好情况,最坏情况,平均情况时间复杂度.
- 要排序的数据有的接近有序,有的完全无序.有序度的不同影响排序的执行时间,需要知道算法在不同有序度的数据下的性能表现.
时间复杂度的系数,常数,低阶.
- 时间复杂度反应的是n很大时执行时间的增长趋势,表示时会忽略系数,常数,低阶.
- 但实际排序场景,可能只会遇到1000以内这样很小的数据规模.所以对于同一阶时间复杂度的不同算法,其系数,常数,低阶都要考虑进来.
比较次数和交换(移动)次数.
- 基于比较的排序算法,一定会涉及元素间的比较及位置交换(或移动).所以要将比较及交换(或移动)次数也考虑进去.

2. 排序算法的内存消耗

和其他算法一样,其内存消耗使用空间复杂度来衡量.
原地排序:特指空间复杂度是O(1)的排序算法.

3. 排序算法的稳定性

稳定性是指: 若待排序的序列中存在值相等的元素,经过排序之后,值相等元素之间原有的先后顺序保持不变.
排序后,值相等元素之间原始顺序不变,称为稳定的排序算法.
排序后,值相等元素之间原始顺序改变,称为不稳定的排序算法.
比如一组数据,要按照attr1属性从大到小排序,attr1属性值相等时,按照attr2属性值从小到大排序.
- 首先按照attr2属性值从小到大排序
- 再利用稳定排序算法,按照attr1从大到小排序.

17. 冒泡排序

1. 冒泡排序只会操作相邻的2个数据.

2. 若相邻的2个元素大小关系不满足要求,则互换.

3. 1次冒泡会让至少1个元素移动到移动到正确位置,重复n次,就完成了n个数据的排序.

public class BubbleSort {
    public void bubbleSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
        int length = arr.length;
        //moved用于标记每一次冒泡是否发生了元素交互,若未发生交互,说明当前数据已经排序完成,可以中止继续比较.
        boolean moved = false;
        int temp;
        for (int i = 0; i < length; i++) {
            moved = false;
            for (int j = 0; j < length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    moved = true;
                }
            }
            if (!moved) {
                System.out.println("冒泡次数:" + (i + 1));
                break;
            }
        }
    }

    public static void main(String[] args) {
        BubbleSort t = new BubbleSort();
        int[] arr = { 12, 54, 32, 8, 6, 3, 111, 45 };
        t.bubbleSort(arr);
        Arrays.stream(arr).forEach(System.out::println);
    }
}

//运行结果:
冒泡次数:6
3
6
8
12
32
45
54
111

4. 冒泡排序的时间复杂度,空间复杂度,稳定性

最好情况时间复杂度: O(n)
- 所有元素都是有序的.
- 冒泡一次并发现无元素交换就终止排序.
最坏情况时间复杂度: O(n^2)
- 所有元素完全是逆序
- n次冒泡.
平均情况时间复杂度: O(n^2)
- 有序度: 原始数组中排序正确的元素对个数
- 满有序度: 原始数组是完全有序的,其有序度称为满有序度
- 逆序度: 原始数组中排序错误的元素对个数
  - 逆序度 = 满有序度 - 有序度
  - 逆序度是原始数组需要执行元素交换的次数
  - 满有序度 = n*(n-1)/2, 逆序度平均就是满有序度/2 = n*(n-1)/4
  - 比较交换次数肯定大于交换次数,且最坏时间复杂度就是O(n^2).所以冒泡排序的平均情况时间复杂度就是O(n^2)
空间复杂度是O(1), 属于稳定排序.

18. 插入排序

1. 插入排序将数组整体分为已排序区间和未排序区间.初始已排序区间只有1个元素,就是数组的第一个元素.

2. 每次取未排序区间头上的元素,在已排序区间中找到合适的位置将其插入,并保证已排序区间一直有序.

3. 重复整个过程,直至未排序区间元素为空.

public class InsertSort {
    public void insertSort(int[] a) {
        if (a == null || a.length <= 1) {
            return;
        }
        int value;
        int j;
        for (int i = 1; i < a.length; i++) {
            value = a[i];
            j = i - 1;
            for (; i >= 0; j--) {
                if(a[j] > value) {
                    a[j + 1] = a[j];
                }else {
                    break;
                }
            }
            a[j + 1] = value;
        }
    }

    public static void main(String[] args) {
        InsertSort t = new InsertSort();
        int[] a = {1,2,31,32,19,18,17,16,61,58,54};
        t.insertSort(a);
        System.out.println("运行结果:\n");
        Arrays.stream(a).forEach(System.out::println);
    }
}

运行结果:

1
2
16
17
18
19
31
32
54
58
61

4. 插入排序最好情况时间复杂度是O(n),最坏情况时间复杂度是O(n^2),平均情况时间复杂度是O(n^2). 空间复杂度是O(1),属于稳定排序.

19. 选择排序

1. 选择排序类似插入排序,也将整个数组分为已排序区间和未排序区间.

2. 每次从未排序区间中找到最小元素,放到已排序区间末尾.

public class SelectSort {
    public void selectSort(int[] a) {
        if (a == null || a.length <= 1) {
            return;
        }
        int minIndex;
        int temp;
        for (int i = 0; i < a.length - 1; i++) {
            minIndex = i;
            for (int j = i + 1; j < a.length; j++) {
                if (a[j] < a[minIndex]) {
                    minIndex = j;
                }
            }
            temp = a[i];
            a[i] = a[minIndex];
            a[minIndex] = temp;
        }
    }

    public static void main(String[] args) {
        SelectSort t = new SelectSort();
        int[] a = { 3, 5, 7, 2, 4, 6, 89, 40 };
        t.selectSort(a);
        System.out.println("选择排序后数组:");
        Arrays.stream(a).forEach(System.out::println);
    }
}

选择排序后数组:
2
3
4
5
6
7
40
89

3. 选择排序的最好,最坏,平均时间复杂度都是O(n^2),因为每次都要完整比较,没有中途退出的机会.

4. 选择排序的空间复杂度是O(1).

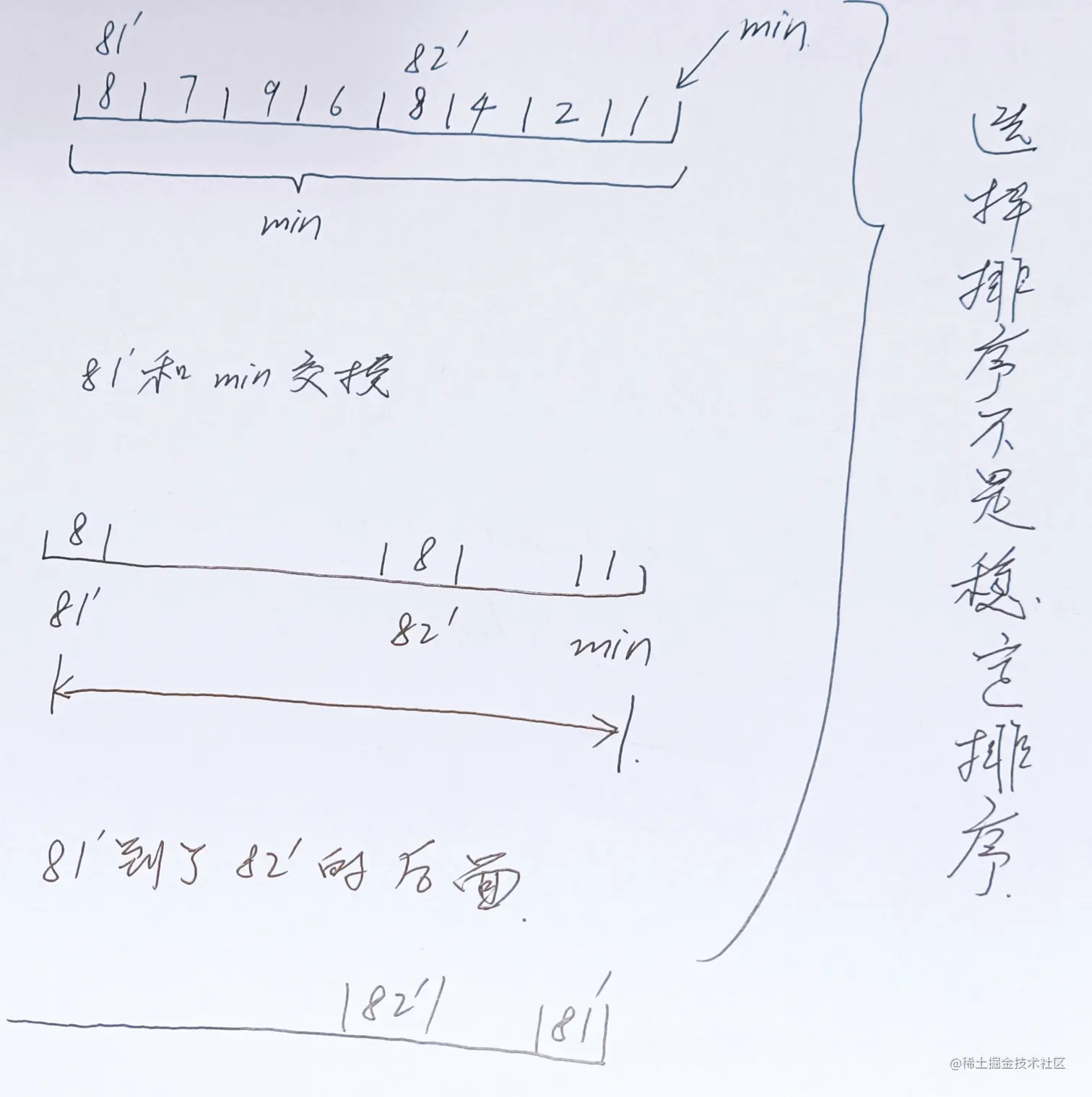
5. 选择排序不是稳定排序,因为min元素要和已排序区间的末尾元素进行交换,有几率导致顺序被打乱. 上图:

选择排序并不是稳定排序.jpg

20. 冒泡排序和插入排序的时间复杂度相同,都是O(n^2).为什么插入排序使用更普遍

1. 两者虽然时间复杂度相同都是O(n^2),但是元素交换操作,插入排序比冒泡排序要简单,代码行数更低,所以插入排序性能更好.

2. 两者元素交换比较

//冒泡排序
if(a[j] > a[j + 1]){
    temp = a[j];
    a[j] = a[j + 1];
    a[j + 1] = temp;
    moved = true;
}

//插入排序
if(a[j] > value){
    a[j + 1] = a[j];
}else{
    break;
}

21. 归并排序

1. 将原始数组分为2部分,2部分排序完成后,将2部分合并

2. 每一部分可以继续分为2部分,递归执行

3. 伪代码

public void sort(int[] arr) {
    splitSort(arr, 0, arr.length - 1);
}
public int[] splitSort(int[] arr, int startIndex, int endIndex) {
    if (startIndex >= endIndex) {
        return new int[] { arr[startIndex] };
    }
    int midIndex = (startIndex + endIndex) / 2;
    int[] a1 = splitSort(arr, startIndex, midIndex);
    int[] a2 = splitSort(arr, midIndex + 1, endIndex);
    int[] result = merge(a1, a2);
    return result;
}
public int[] merge(int[] a1, int[] a2) {
    int[] result = new int[a1.length + a2.length];
    int i1 = 0;
    int i2 = 0;
    for (int i = 0; i < result.length; i++) {
        if (a1[i1] > a2[i2]) {
            result[i] = a2[i2];
            i2++;
        } else {
            result[i] = a1[i1];
            i1++;
        }
    }
    return result;
}

4. 归并排序的时间复杂度是O(nlogn),很稳定

5. 归并排序的空间复杂度是O(n),因为合并数组数组需要创建新的数组,所以不是原地排序.

6. 归并排序属于稳定排序.比如a1和a2中有相同值的元素,按照约定将a1的元素先加到合并后的数组中.

22. 快速排序

1. 快速排序,是每次取数组中的一个元素作为分区值,数组中元素值,小于该值的放到其左边,大于该值的放到其右边.

2. 然后对其左边及右边再分别进行排序,递归执行.

3. 伪代码

public void sort(int[] arr){
    quickSort(arr, 0, arr.length - 1);
}
public void quickSort(int[] arr, int startIndex, int endIndex){
    if(arr == null || startIndex >= endIndex){
        return;
    }
    int pivot = partition(arr, startIndex, endIndex);
    quickSort(arr, startIndex, pivot - 1);
    quickSort(arr, pivot + 1, endIndex);
}
public int partition(int[] arr, int startIndex, int endIndex){
    int value = arr[endIndex];
    int pivot = endIndex;
    for(int i = startIndex; i<endIndex - 1; i++){
        if(a[i] < value){
            if(pivot == endIndex){
                if(i != startIndex){
                    swap(i, startIndex);
                }
                pivot = startIndex;
            }else{
                swap(pivot+1, i);
                pivot++;
            }
        }
    }
    if(pivot != endIndex){
        pivot = pivot + 1;
        swap(endIndex, pivot);
    }
    return pivot;
}

4. 快速排序的时间复杂度是O(nlogn),最差时间复杂度是O(n^2).

5. 快速排序是原地排序,因为不涉及创建新的数组,直接对数组元素进行排序.

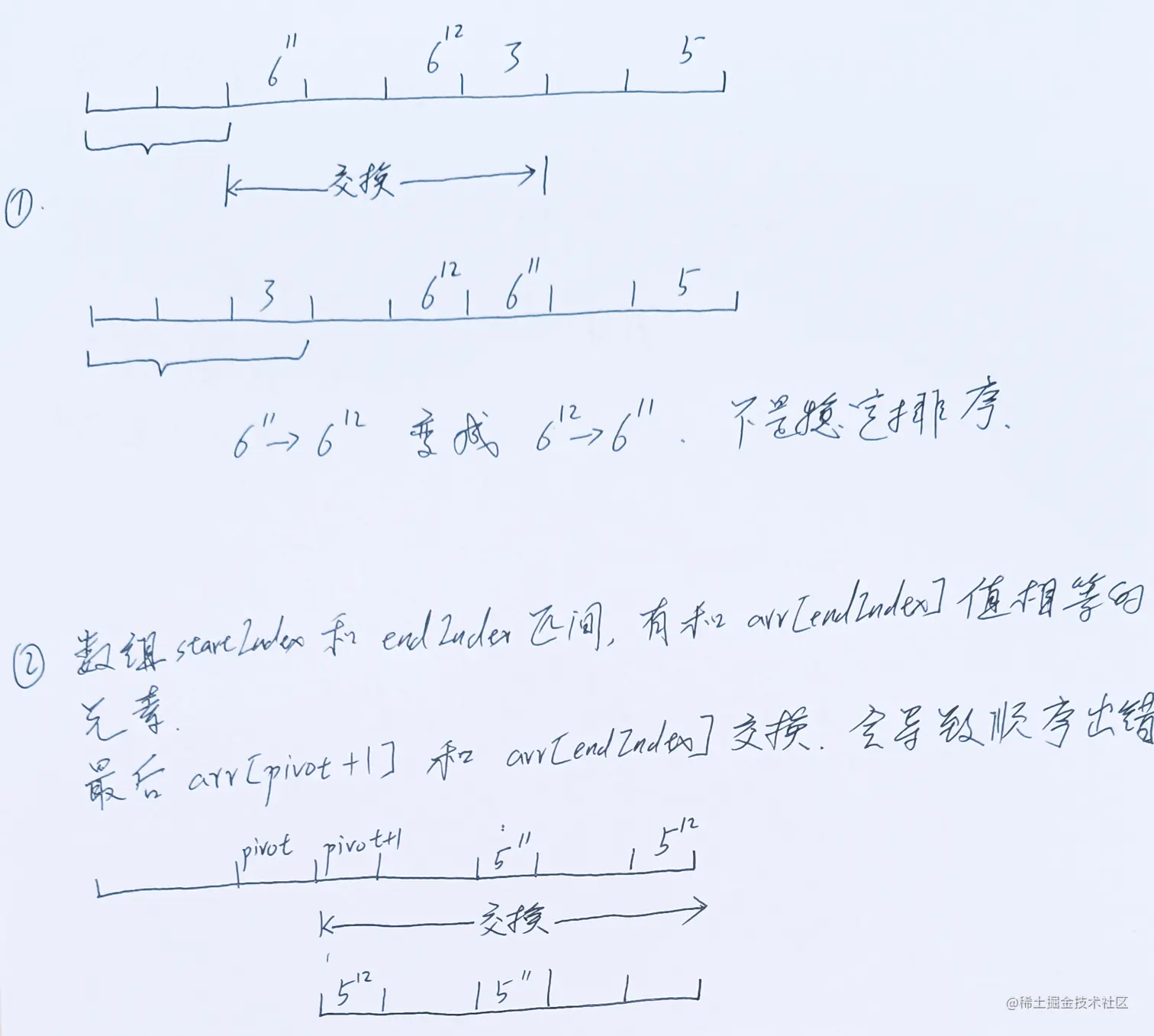
6. 款速排序不是稳定排序,设计到数组元素的交换.有2种情况会导致相同值的元素顺序改变.

快排不是稳定排序

数据结构与算法总结 - 第一篇

1. 10个最常用的数据结构

2. 10个最常用的算法

3. 数据结构和算法的关系

4. 常见的时间复杂度

5. 时间复杂度称为渐进时间复杂度,表示算法的执行时间随数据规模的增长关系.

6. 空间复杂度称为渐进空间复杂度,表示算法的存储空间随数据规模的增长关系.

7. 线性表

8. 非线性表

9. 数组

10. 链表: 通过指针将一组零散的内存块串联在一起.

11. 数组和链表的比较

12. 链表的几个问题

1. 单链表实现LRU

2. 上面的例子引出1个认识误区

3. 约瑟夫问题 一道阿里笔试题：我是如何用一行代码解决约瑟夫环问题的

3.1. 使用数组解决

3.2. 使用循环列表解决

4. 数组实现LRU

5. 自定义单链表,校验字符是否是回文字符串

6. 单链表反转

7. 两个有序单链表的合并

8. 删除单链表倒数第K个结点

9. 求单链表的中间节点

13. 栈 : 一种操作受限的线性表结构,仅支持单方向的入栈及出栈.

1. 用2个栈来实现浏览器的前进及回退

2. 使用链表实现栈

3.使用2个栈来实现浏览器的 打开,前进,后退 功能

14. 队列: 一种操作受限的线性表,先进先出,就是典型的队列.

1. 入队: 向队列尾部添加1个元素

2. 出队: 从队列头部取1个元素

3. 构建以数组为基础的队列

4. 构建以数组为基础的队列,只要数组有剩余空间,就可以继续添加元素

5. 构建以链表为基础的队列,无界队列

6. 构建以数组为基础的循环队列

15. 递归

1. 可以用递归解决的问题需满足的条件

2. 递归的缺点

3. 几个递归问题

3.1. n阶楼梯,每次可以上1阶或者上2阶,一共有多少种走法?

16. 如何评价1个排序算法: 从 排序算法的执行效率, 排序算法的空间复杂度, 排序算法的稳定性 3个方面来衡量.

1. 排序算法的执行效率

2. 排序算法的内存消耗

3. 排序算法的稳定性

17. 冒泡排序

1. 冒泡排序只会操作相邻的2个数据.

2. 若相邻的2个元素大小关系不满足要求,则互换.

3. 1次冒泡会让至少1个元素移动到移动到正确位置,重复n次,就完成了n个数据的排序.

4. 冒泡排序的时间复杂度,空间复杂度,稳定性

18. 插入排序

1. 插入排序将数组整体分为已排序区间和未排序区间.初始已排序区间只有1个元素,就是数组的第一个元素.

2. 每次取未排序区间头上的元素,在已排序区间中找到合适的位置将其插入,并保证已排序区间一直有序.

3. 重复整个过程,直至未排序区间元素为空.

4. 插入排序最好情况时间复杂度是O(n),最坏情况时间复杂度是O(n^2),平均情况时间复杂度是O(n^2). 空间复杂度是O(1),属于稳定排序.

19. 选择排序

1. 选择排序类似插入排序,也将整个数组分为 已排序区间 和 未排序区间.

2. 每次从未排序区间中找到最小元素,放到 已排序区间末尾.

3. 选择排序的最好,最坏,平均时间复杂度都是O(n^2),因为每次都要完整比较,没有中途退出的机会.

4. 选择排序的空间复杂度是O(1).

5. 选择排序不是稳定排序,因为min元素要和已排序区间的末尾元素进行交换,有几率导致顺序被打乱. 上图:

20. 冒泡排序和插入排序的时间复杂度相同,都是O(n^2).为什么插入排序使用更普遍

1. 两者虽然时间复杂度相同都是O(n^2),但是元素交换操作,插入排序比冒泡排序要简单,代码行数更低,所以插入排序性能更好.

2. 两者元素交换比较

21. 归并排序

1. 将原始数组分为2部分,2部分排序完成后,将2部分合并

2. 每一部分可以继续分为2部分,递归执行

3. 伪代码

4. 归并排序的时间复杂度是O(nlogn),很稳定

5. 归并排序的空间复杂度是O(n),因为合并数组数组需要创建新的数组,所以不是原地排序.

6. 归并排序属于稳定排序.比如a1和a2中有相同值的元素,按照约定将a1的元素先加到合并后的数组中.

22. 快速排序

1. 快速排序,是每次取数组中的一个元素作为分区值,数组中元素值,小于该值的放到其左边,大于该值的放到其右边.

2. 然后对其左边 及 右边 再分别进行排序,递归执行.

3. 伪代码

4. 快速排序的时间复杂度是O(nlogn),最差时间复杂度是O(n^2).

5. 快速排序是原地排序,因为不涉及创建新的数组,直接对数组元素进行排序.

6. 款速排序不是稳定排序,设计到数组元素的交换.有2种情况会导致相同值的元素顺序改变.

3. 约瑟夫问题一道阿里笔试题：我是如何用一行代码解决约瑟夫环问题的

3.使用2个栈来实现浏览器的打开,前进,后退功能

16. 如何评价1个排序算法: 从排序算法的执行效率, 排序算法的空间复杂度, 排序算法的稳定性 3个方面来衡量.

1. 选择排序类似插入排序,也将整个数组分为已排序区间和未排序区间.

2. 每次从未排序区间中找到最小元素,放到已排序区间末尾.

2. 然后对其左边及右边再分别进行排序,递归执行.