今天一项工作要处理坐标变换，简单研究了下。
局部坐标系到全局坐标系
原理如下：
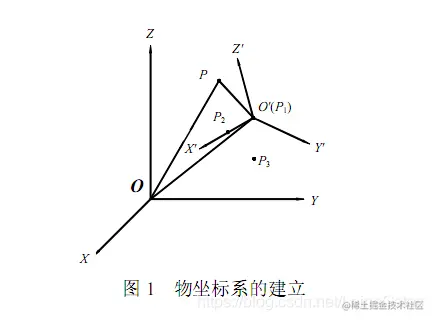图中，世界坐标系是(X,Y,Z)，局部坐标系是(X′,Y′,Z′)，局部坐标系原点O′。
要转换的点是P。
OP=x∗i+y∗j+z∗kOO′=a∗i+b∗j+c∗k
坐标轴对应关系
⎩⎨⎧i′=u11∗i+u12∗j+u13∗kj′=u21∗i+u22∗j+u22∗kk′=u31∗i+u32∗j+u33∗k
联立公式
O′P=x′∗i′+y′∗j′+z′∗k′=x′∗(u11∗i+u12∗j+u13∗k)+y′∗(u21∗i+u22∗j+u22∗k)+z′∗(u31∗i+u32∗j+u33∗k)=(u11∗x′+u21∗y′+u31∗z′)∗i+(u12∗x′+u22∗y′+u32∗z′)∗j+(u13∗x′+u23∗y′+u33∗z′)∗k
OP=OO′+O′P ，于是
⎩⎨⎧x=a+u11∗x′+u21∗y′+u31∗z′y=b+u12∗x′+u22∗y′+u32∗z′z=c+u13∗x′+u23∗y′+u33∗z′
得转换关系
[xyz1]=[x′y′z′1]∗W
最终获得矩阵
W=⎣⎡u11u21u31au12u22u32bu13u23u33c0001⎦⎤
全局坐标系到局部坐标系
因为
[xyz1]=[x′y′z′1]∗W
那么
[xyz1]∗W−1=[x′y′z′1]
观察到
W=⎣⎡u11u21u31au12u22u32bu13u23u33c0001⎦⎤=⎣⎡u11u21u310u12u22u320u13u23u3300001⎦⎤⋅⎣⎡100a010b001c0001⎦⎤=R⋅T
其中，R是旋转矩阵，T是平移矩阵
那么
W−1=(R⋅T)−1=T−1∗R−1
其中
T−1=⎣⎡100−a010−b001−c0001⎦⎤
如果R是正定矩阵，即R⋅R−1=E。那么
R−1=RT=⎣⎡u11u12u130u21u22u230u31u32u3300001⎦⎤
直接可计算W−1。
但如果R不是正定方阵，即局部坐标系的坐标轴不是右手系相互垂直的，那么还是直接求逆得W−1。
