吴恩达机器学习-4-神经网络基础
在本周中主要讲解的是神经网络-Neural Networks的基础知识:
- 非线性假设
- 神经元和大脑
- 模型表示
- 特征和直观理解
- 多类分类问题
非线性假设Non-linear Hypotheses
线性回归和逻辑回归的缺点:特征太多的时候,计算负荷会非常大
假设我们希望训练一个模型来识别视觉对象(例如识别一张图片上是否是一辆汽车),我们怎样才能这么做呢?一种方法是我们利用很多汽车的图片和很多非汽车的图片,然后利用这些图片上一个个像素的值(饱和度或亮度)来作为特征。

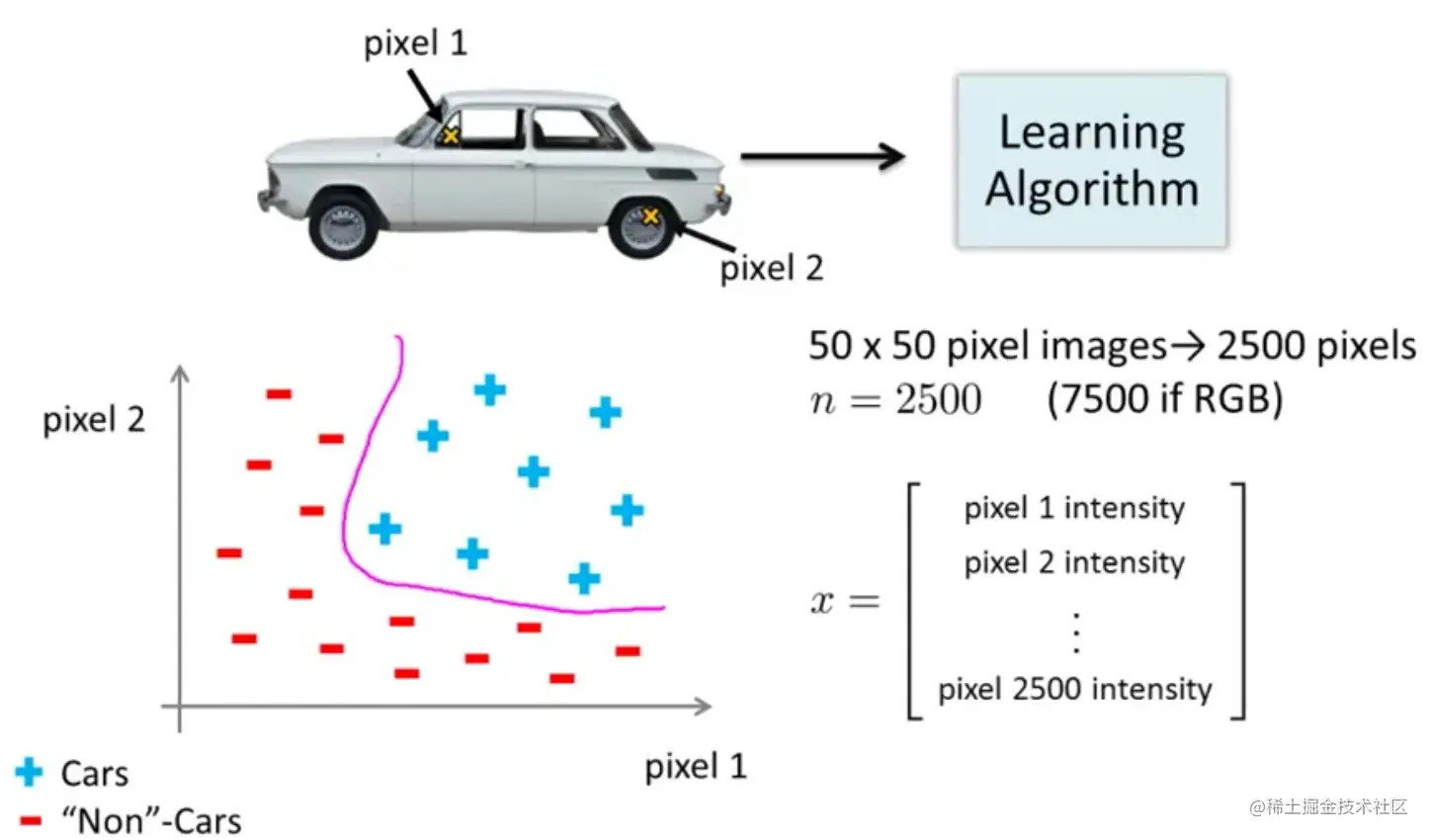
假设采用的是50*50像素的小图片,将所有的像素视为特征,则有2500个特征。普通的逻辑回归模型不能处理的,需要使用神经网络
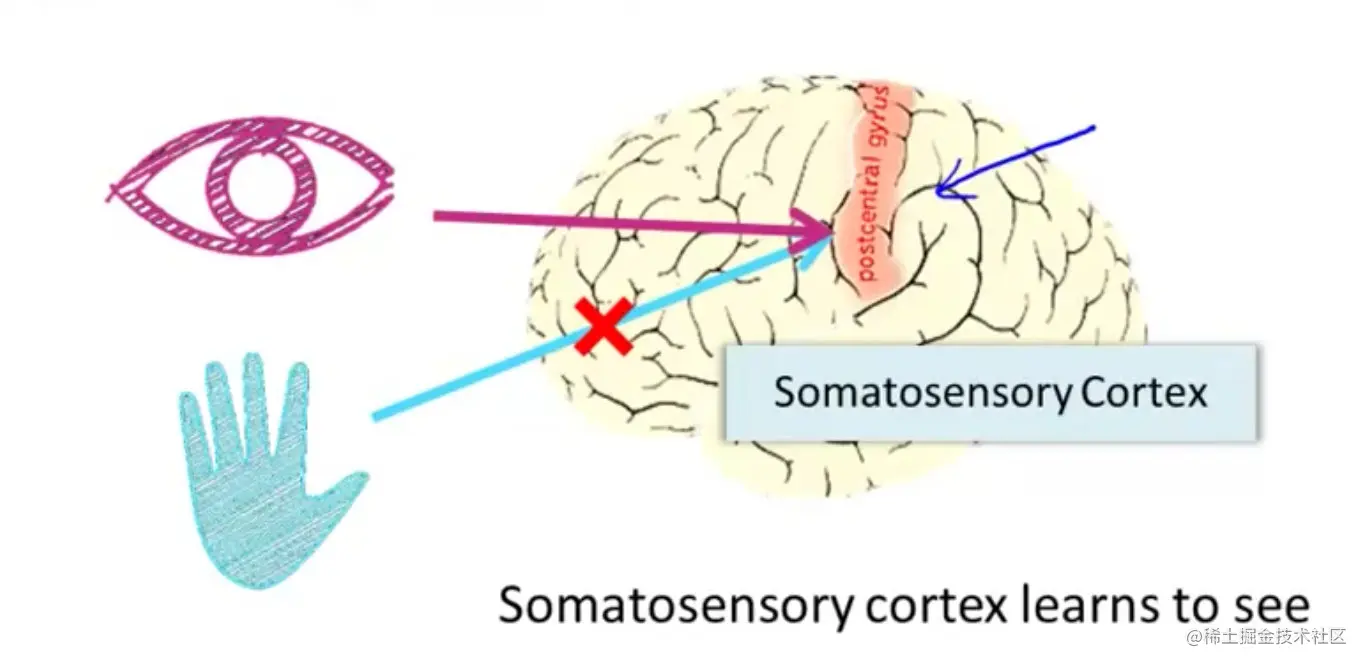
神经元和大脑
模型表示
模型表示1
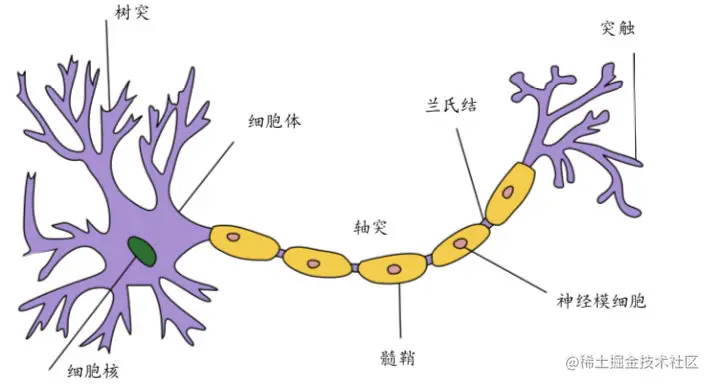
每个神经元是可以被认为一个处理单元/神经核processing unit/Nucleus,主要包含:
- 多个输入/树突
input/Dendrite
- 一个输出/轴突
output/Axon
神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络
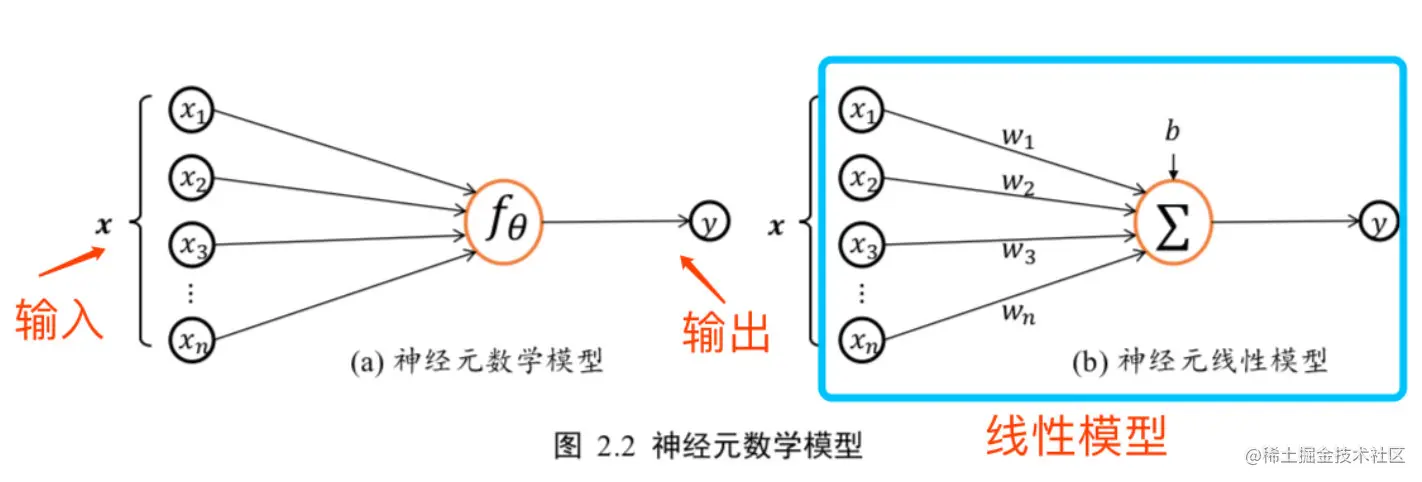
- 神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型
- 神经元称之为激活单元activation unit;在神经网络中,参数又可被成为权重(weight)
- 类似神经元的神经网络
神经网络
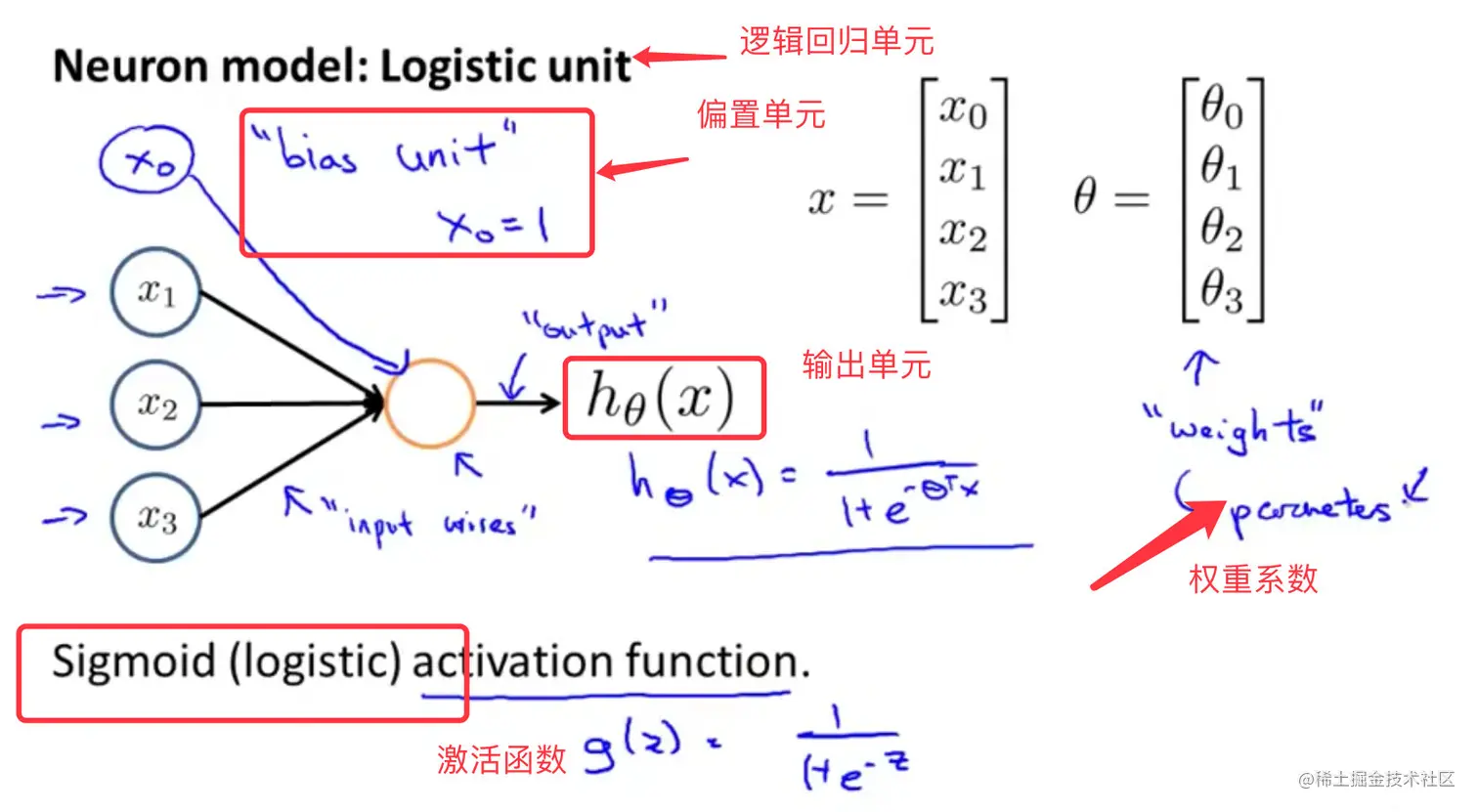
下图是逻辑回归模型作为自身学习模型的神经元示例
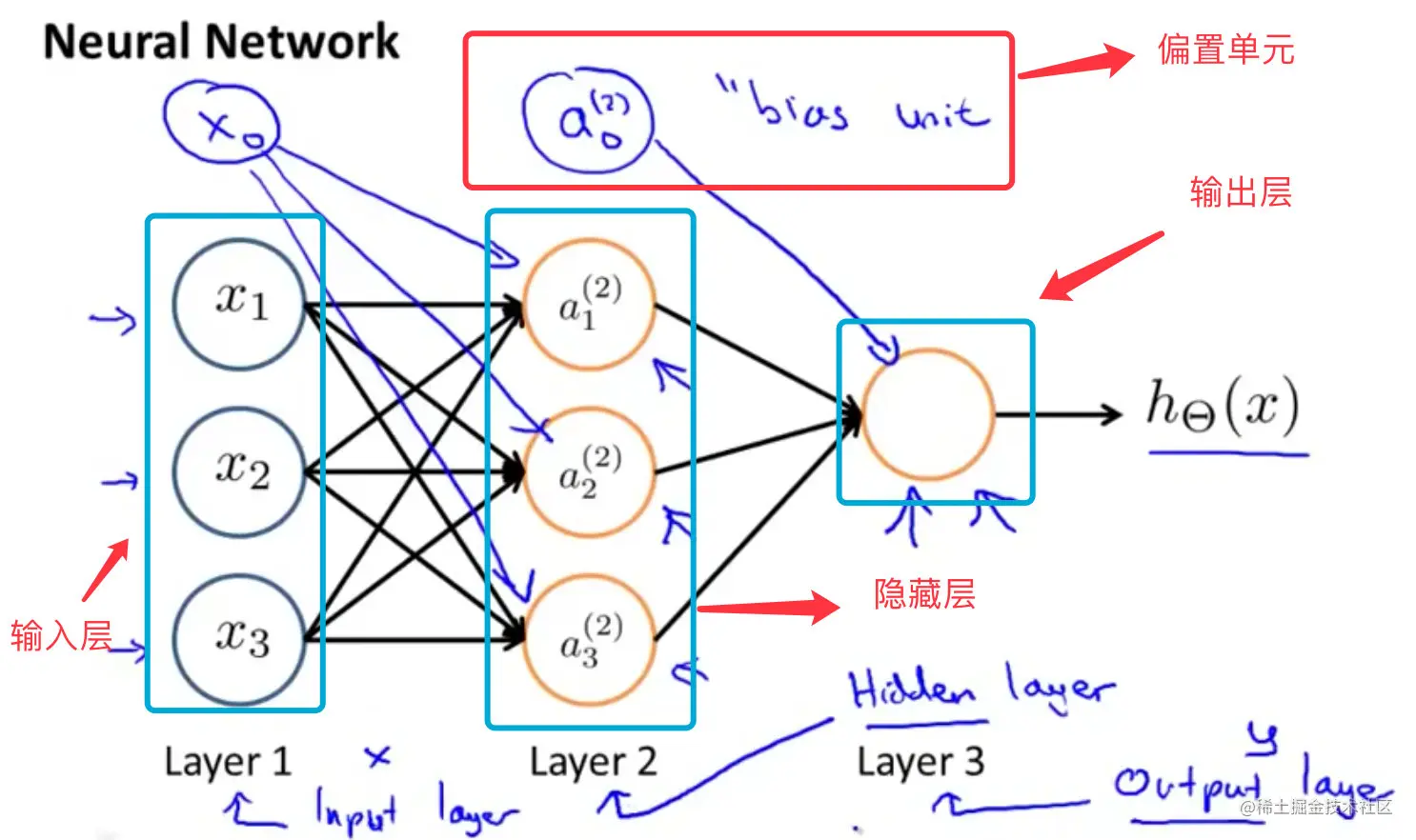
类似神经元的神经网络结构
-
x1,x2,x3是输入单元,将原始数据输入给它们
-
几个比较基础的概念
- 输入层:数据节点所在的层
- 网络层:输出hi连同它的网络层参数w,b
- 隐藏层:网络层中间的层
- 输出层:最后一层
- 偏置单元:
bias unit,每层加上偏置单元
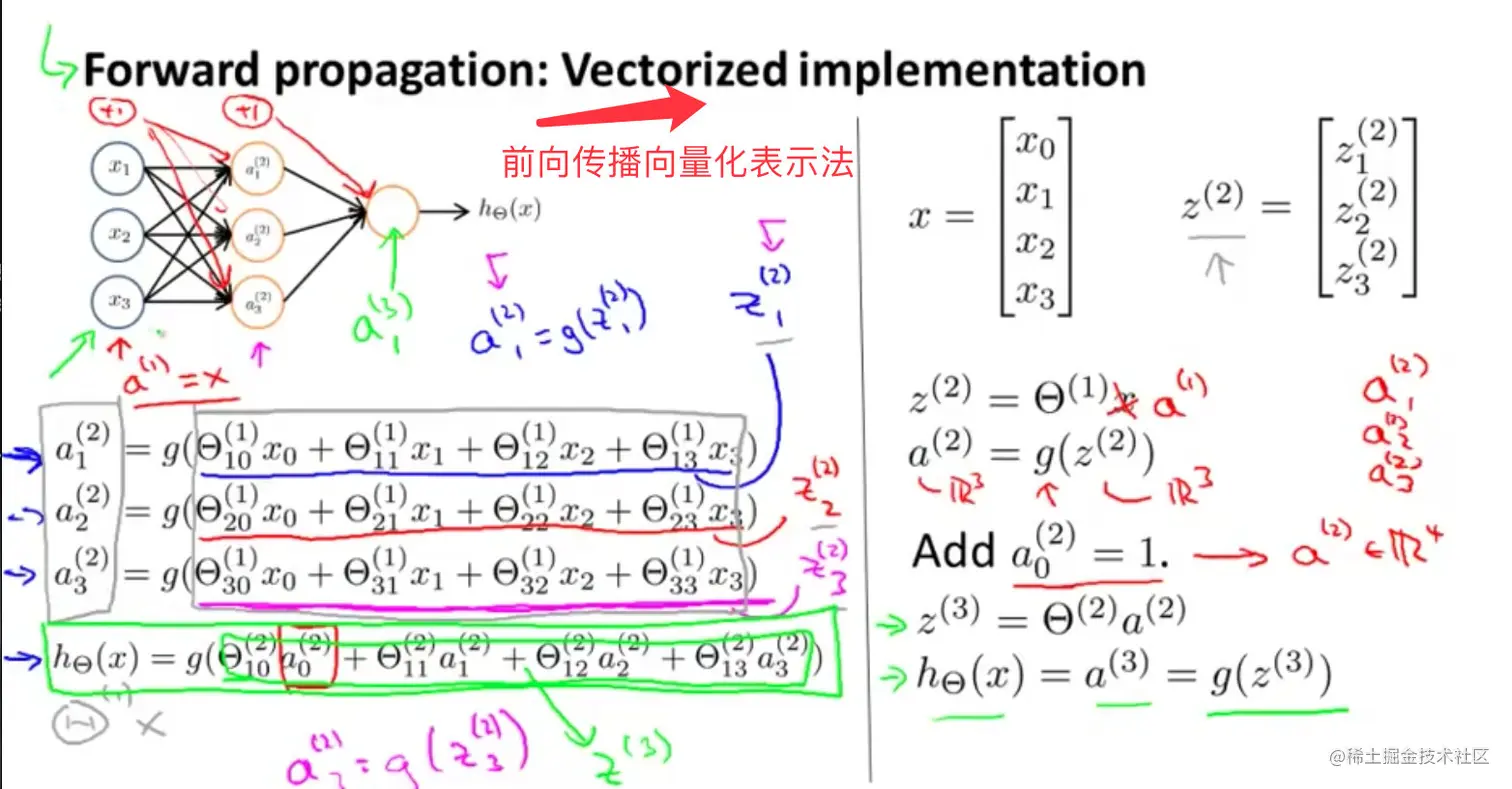
上面模型的激活单元和输出分别表示为:
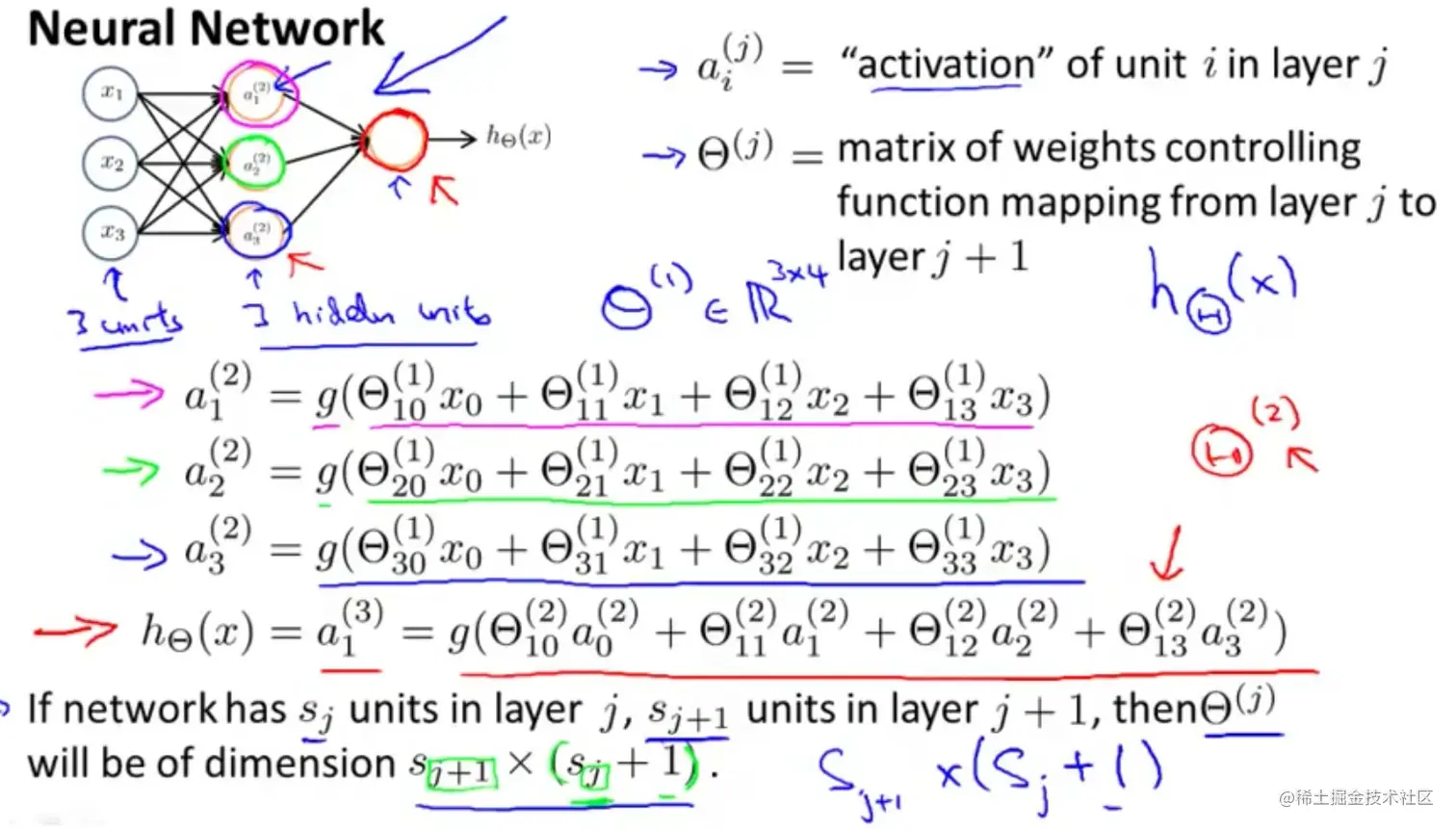
三个激活单元的表达式:
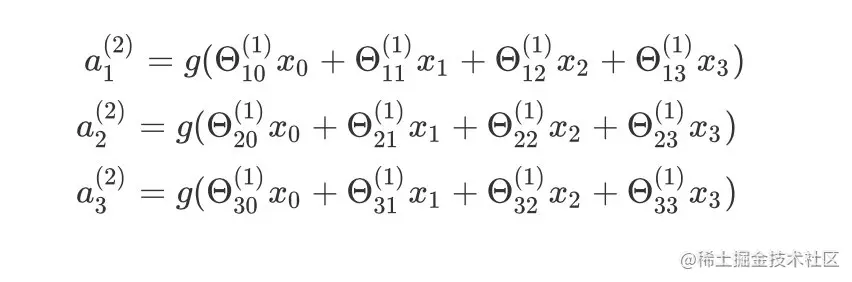
a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
输出的表达式为:
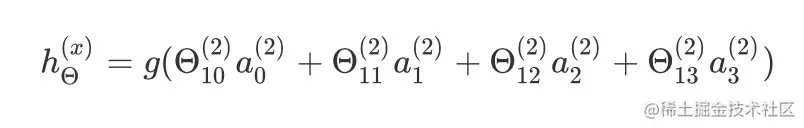
hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
将特征矩阵的每行(一个训练实例)喂给了神经网络,最终需要将整个训练集都喂给神经网络。
这种从左到右计算的算法称之为:前向传播法FORWARD PROPAGATION
模型标记的记忆方法
ai(j)表示的是第j层的第i个激活单元
θ(j)代表从第j层映射到第j+1层的权重矩阵;例如:上图所示的神经网络中θ(1)的尺寸为 3*4。其尺寸具体表示为:
- 以第j 层的激活单元数量为行数
- 以第 j+1层的激活单元数+1为列数的矩阵
模型表示2
FORWARD PROPAGATION相对于使用循环来编码,利用向量化的方法会使得计算更为简便,
假如现在有:
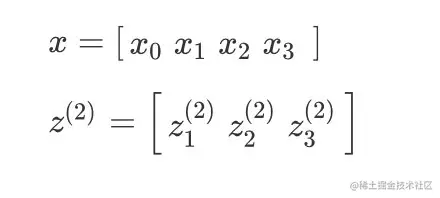
x=[x0 x1 x2 x3 ]
z(2)=[z1(2) z2(2) z3(2)]
其中z满足:
z(2)=Θ(1)x
也就是上面三个激活单元式子中的括号里面部分,那么有:
a(2)=g(z(2))
将输入x看成是a(1),则有:
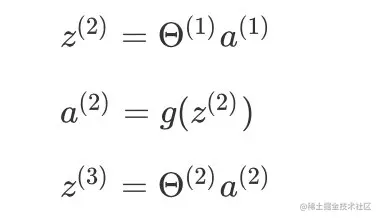
z(2)=Θ(1)a(1)
a(2)=g(z(2))
z(3)=Θ(2)a(2)
那么输出h可以表示为 :
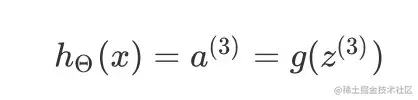
hΘ(x)=a(3)=g(z(3))
特征和直观理解
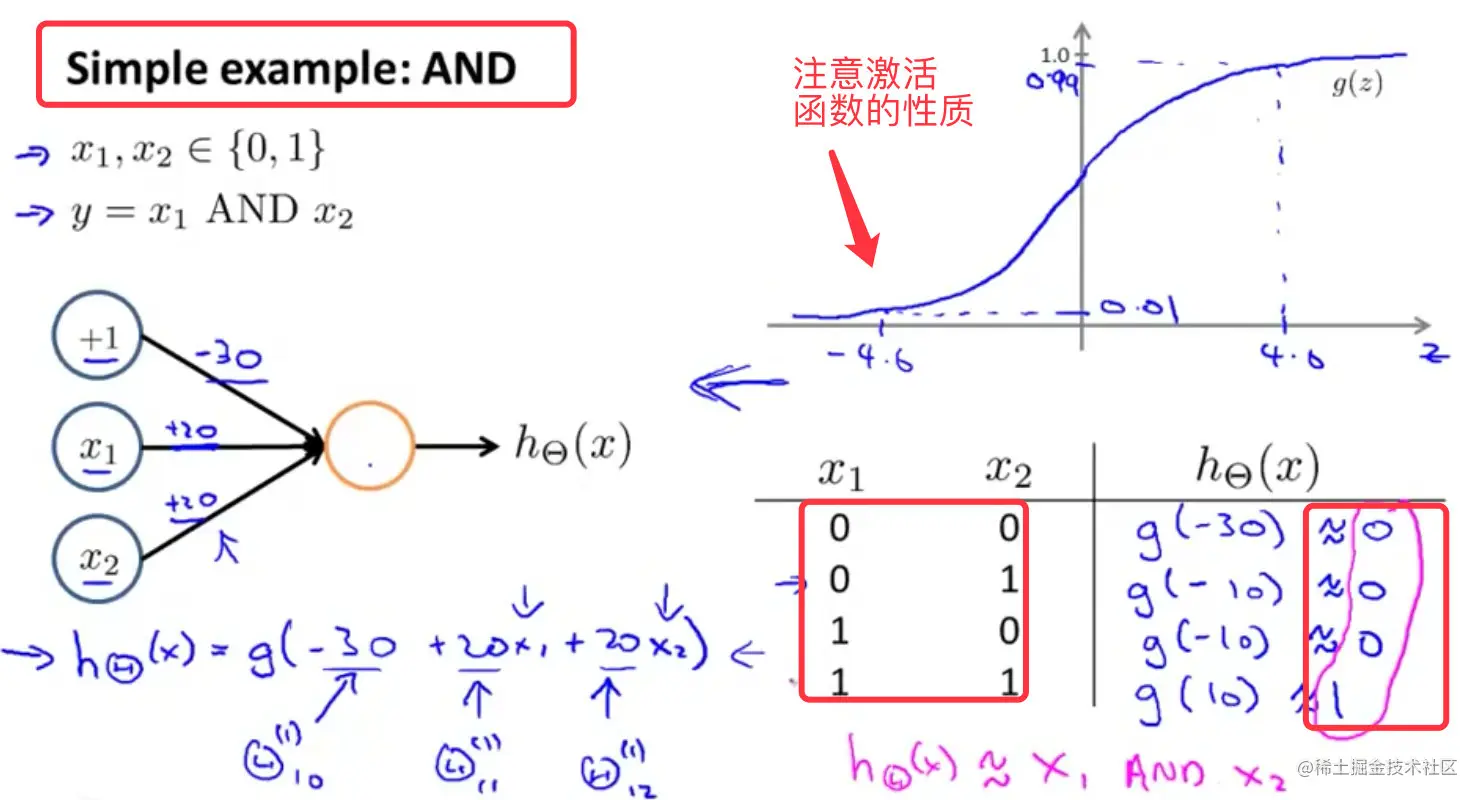
神经网络中,单层神经元(无中间层)的计算可用来表示逻辑运算,比如逻辑与(AND)、逻辑或(OR)
实现逻辑”与AND”
实现逻辑"或OR"

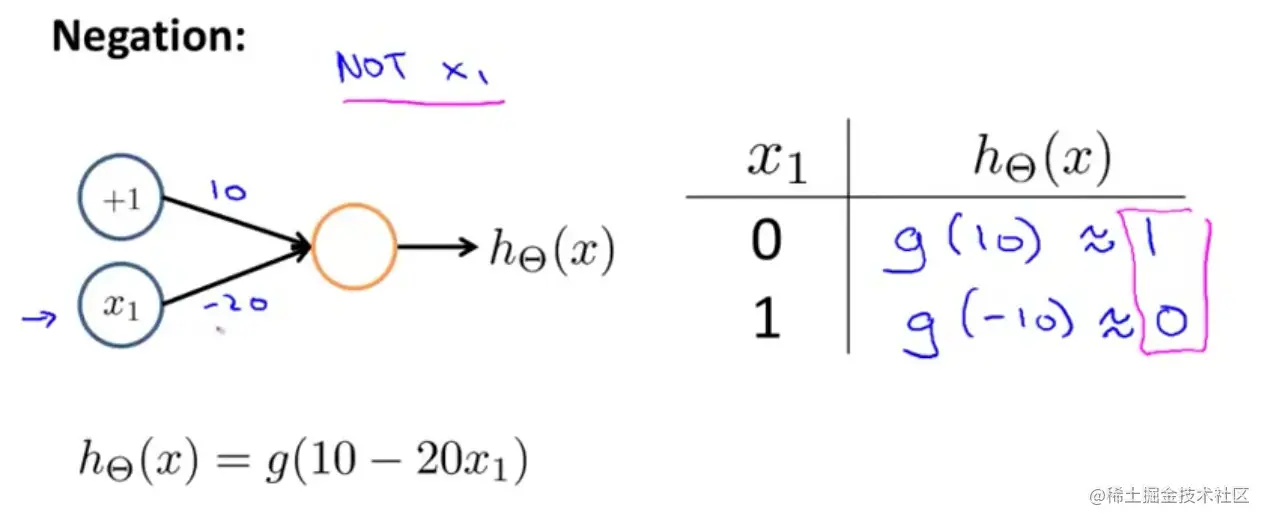
实现逻辑“非not”
多类分类问题
当输出中不止有两种分类时,比如使用神经网络算法来识别路人、汽车、摩托车等。
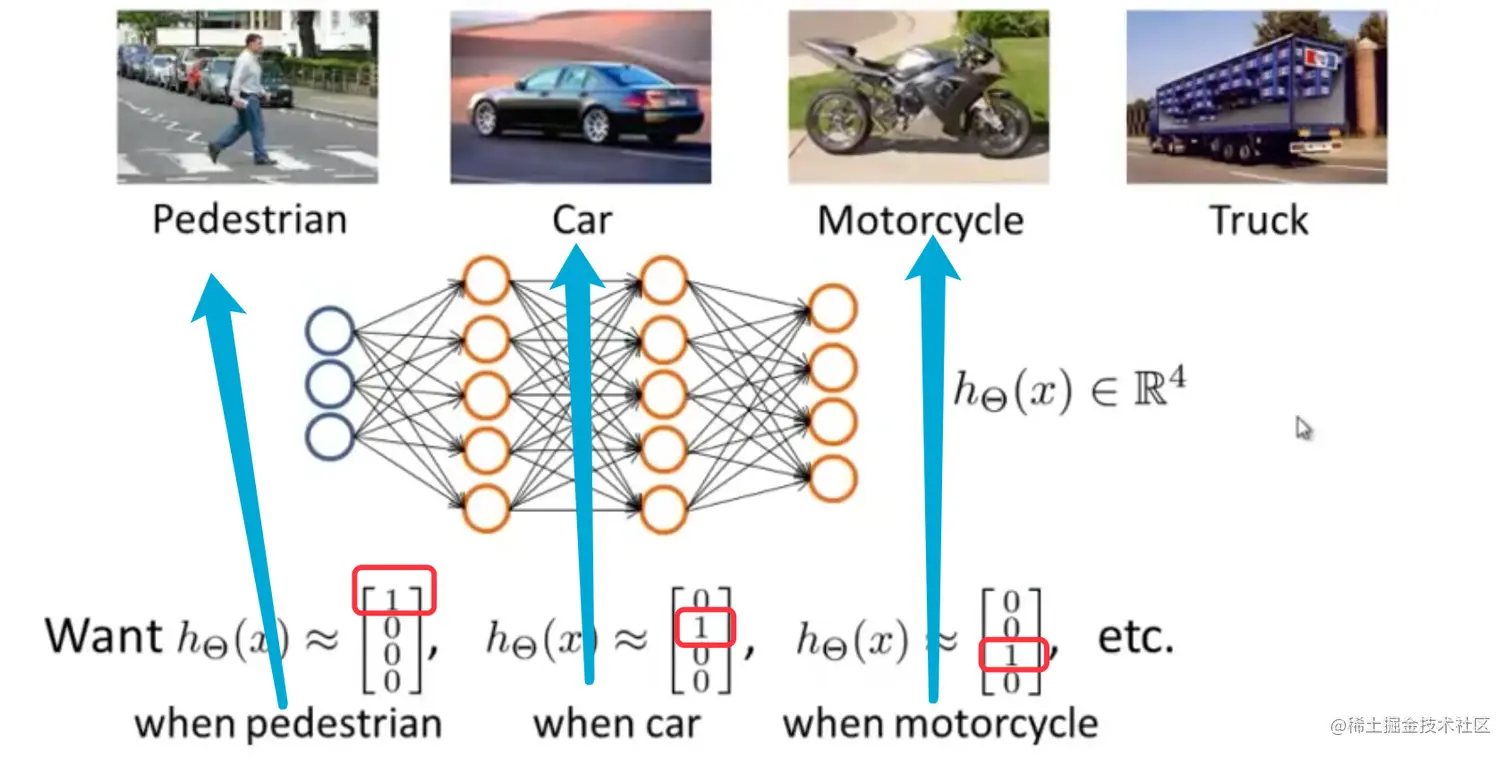
- 输入向量有3个维度,两个中间层
- 输出层有4个神经元表示4种分类,也就是每一个数据在输出层都会出现[a,b,c,d]T,且[a,b,c,d]中仅有一个为1,表示当前类
TF中解决办法
上述多类分类问题和TF中手写数字问题类似,解决办法如下:
- 将输出设置为dout个输出节点的向量,dout与类别数相同
- 让第i∈[1,dout]个输出值表示当前样本属于类别i的概率P
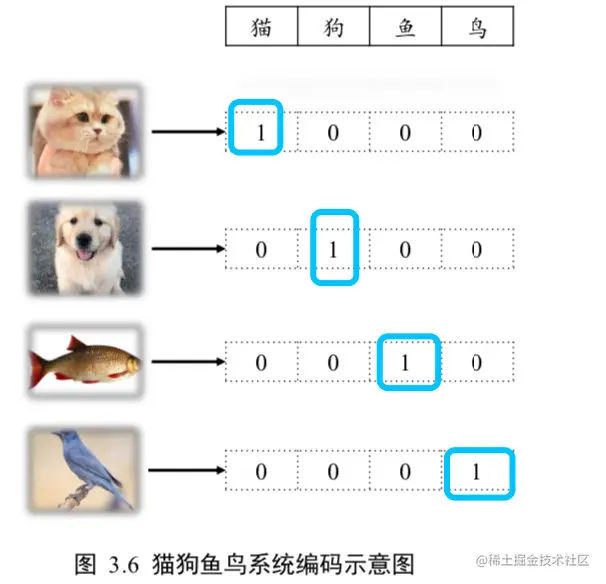
- 如果属于第i类,索引为i的位置设置为1,其余为0!!!!
- 下图中:对于所有猫的图片,数字编码是0,one-hot编码为[1,0,0,0];其他类推
- 手写数字图片数据
总类别数是10,即输出节点总数值dout=10,假设某个样本的类别是i,即图片中的数字是i,需要一个长度为10的向量y,索引号为i的位置设置为1,其余是0。
- 0的one-hot编码是[1,0,0,0,….]
- 1的one-hot编码是[0,1,0,0,….]
- 其余类推