【Leetcode】70. 爬楼梯

题目描述

// 70. 爬楼梯

// 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

// 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
// 注意：给定 n 是一个正整数。

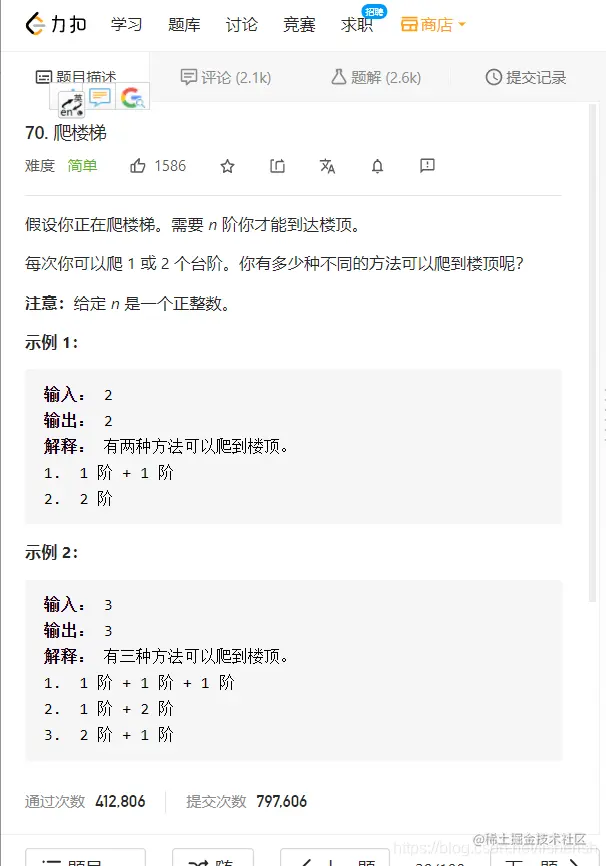
题解

// 跟【剑指offer】10.2. 青蛙跳台阶问题 一样的
// 假设到n阶有f(n)种方法，由于只能走1阶，和走2阶，所以第一步只有两种可能，
// 假设第一步走1阶，还剩n-1阶，有f(n - 1)方法，假设第一步走2阶，
// 还剩n-2阶，有f(n - 2)方法，f(n)实际就是这两种情况各自所有可能的走法，相加。
// 那么有f(n - 1) + f(n - 2) = f(n)。
//
// 执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗：35.1 MB, 在所有 Java 提交中击败了83.44%的用户
class Solution {
    public int climbStairs(int n) {
        if (n == 0)
            return 1;
        if (n <= 2)
            return n;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n - 1];
    }
}


// 执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
// 内存消耗：35.3 MB, 在所有 Java 提交中击败了40.10%的用户
class Solution {
    public int climbStairs(int n) {
        if (n == 0)
            return 1;
        if (n <= 2)
            return n;
        int a = 1;
        int b = 2;
        int f = 0;
        for (int i = 2; i < n; i++) {
            f = a + b;
            a = b;
            b = f;
        }
        return f;
    }
}