207. 课程表

题目

思路

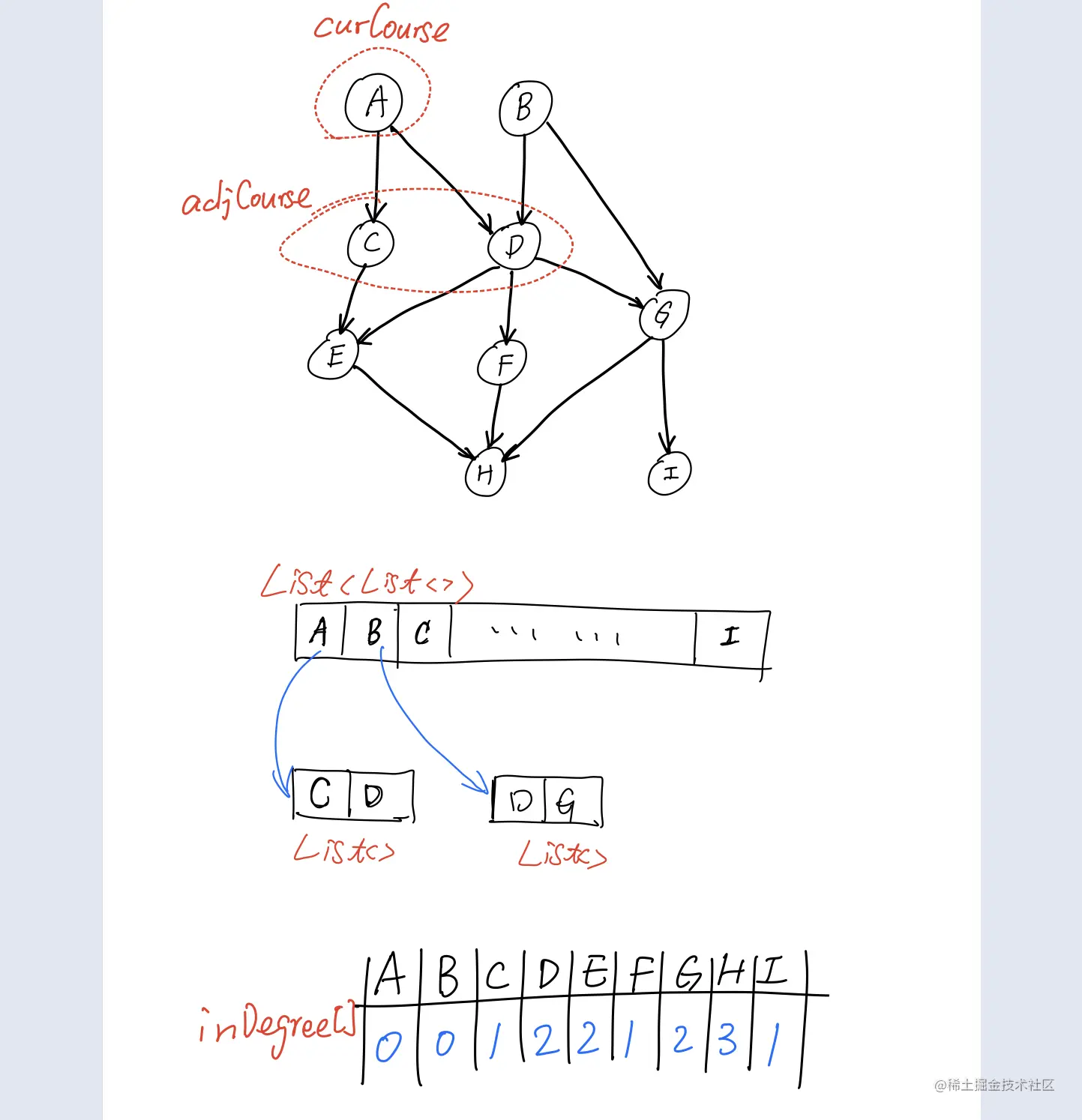
• 根据课程间的依赖关系建立一个有向图， 用List<List<Integer>>, Integer表示课程号。
  • 如果图中有环，说明存在循环依赖，返回false
• 建图的同时统计图中每个节点的入度，生成入度表inDegree
• 维护一个queue，表示当前不需要前置课程可以开始学习的课，即：将所有入度为0的节点加入queue
  • 每入queue一门课，count + 1
  • queue非空时，依次将队首节点出队，记为curCourse，然后把它所有的后继课程adjCourse们的入度-1
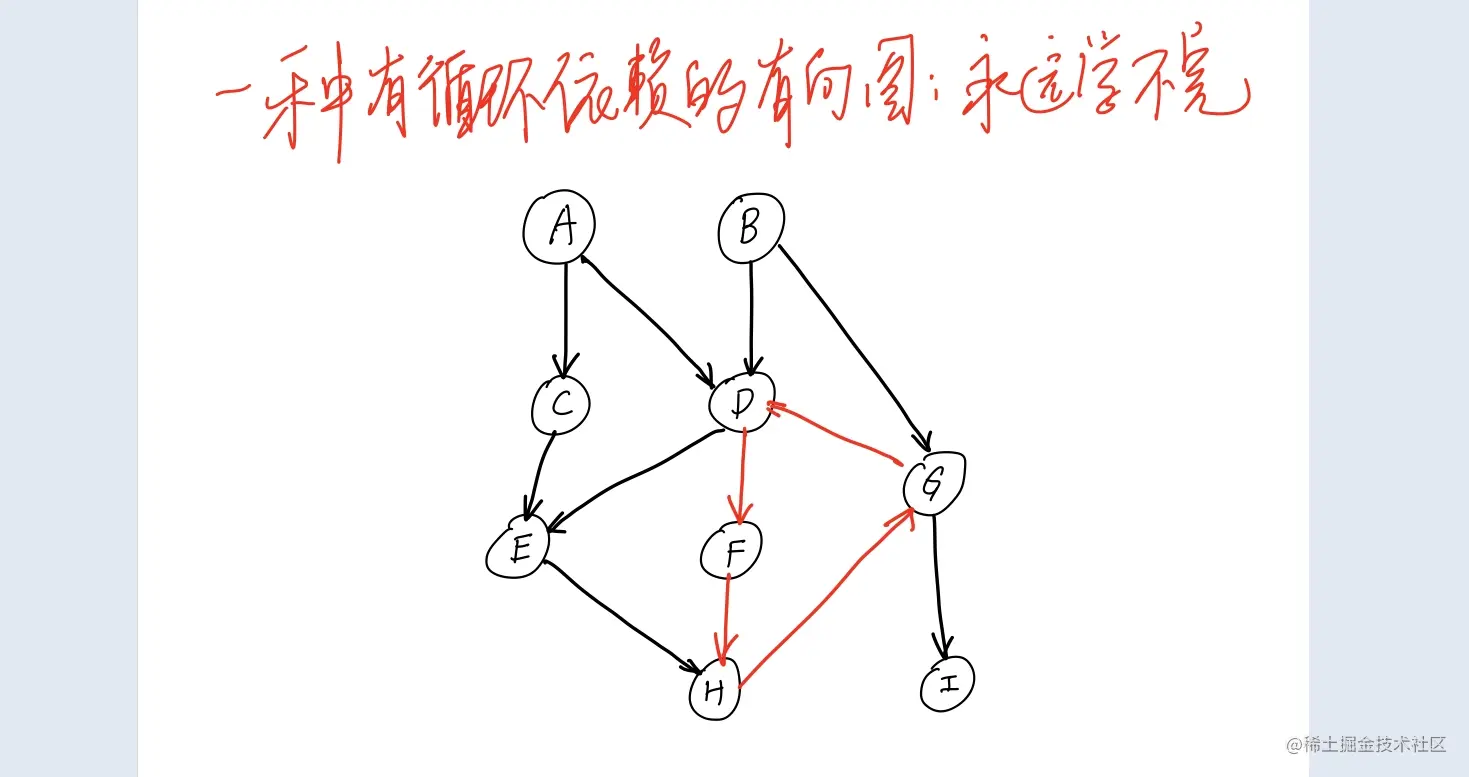
  • 如果存在环，则肯定有课程入度永远不为零，永远无法被加入queue。那么，当queue空时，count不会等于课程总数。

代码

//课程用0,1,2,...numCourse-1表示
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<List<Integer>> graph = new ArrayList<>();//图
        int[] inDegree = new int[numCourses];//入度表
        //初始化每个课程的后继课程list
        for (int i = 0; i < numCourses; i++) {
            graph.add(new ArrayList<>());
        }
        //根据依赖关系prerequisites建立有向图，更新入度表
        for (int[] arr : prerequisites) {
            graph.get(arr[1]).add(arr[0]);//把当前课程的后继课程添加到list中
            inDegree[arr[0]]++;//后继课程的入度+1
        }
        //初始化可学课程队列，入度为0的课程可学
        LinkedList<Integer> queue = new LinkedList<>();
        for (int i = 0; i < inDegree.length; i++) {//i表示0到courseNum-1的课程
            if (inDegree[i] == 0) {
                queue.add(i);//找到所有入度为0的课程，加入队列，表示可以学了
            }
        }
        int count = 0;//学过的课程计数
        //从可学队列中拿出一门课，更新入度表
        while (!queue.isEmpty()) {
            int curCourse = queue.removeFirst();
            count++;
            for (int adjCourse : graph.get(curCourse)) {//adjCourse为当前课程的后继课程
                inDegree[adjCourse]--;//学完当前课程，后继课程的入度都-1
                if (inDegree[adjCourse] == 0) {//如果后继课程入度也为0了，加入可学队列
                    queue.add(adjCourse);
                }
            }
        }
        return count == numCourses;//如果学过的课数量 = 一开始要学的数量，true
    }
}