221. 最大正方形

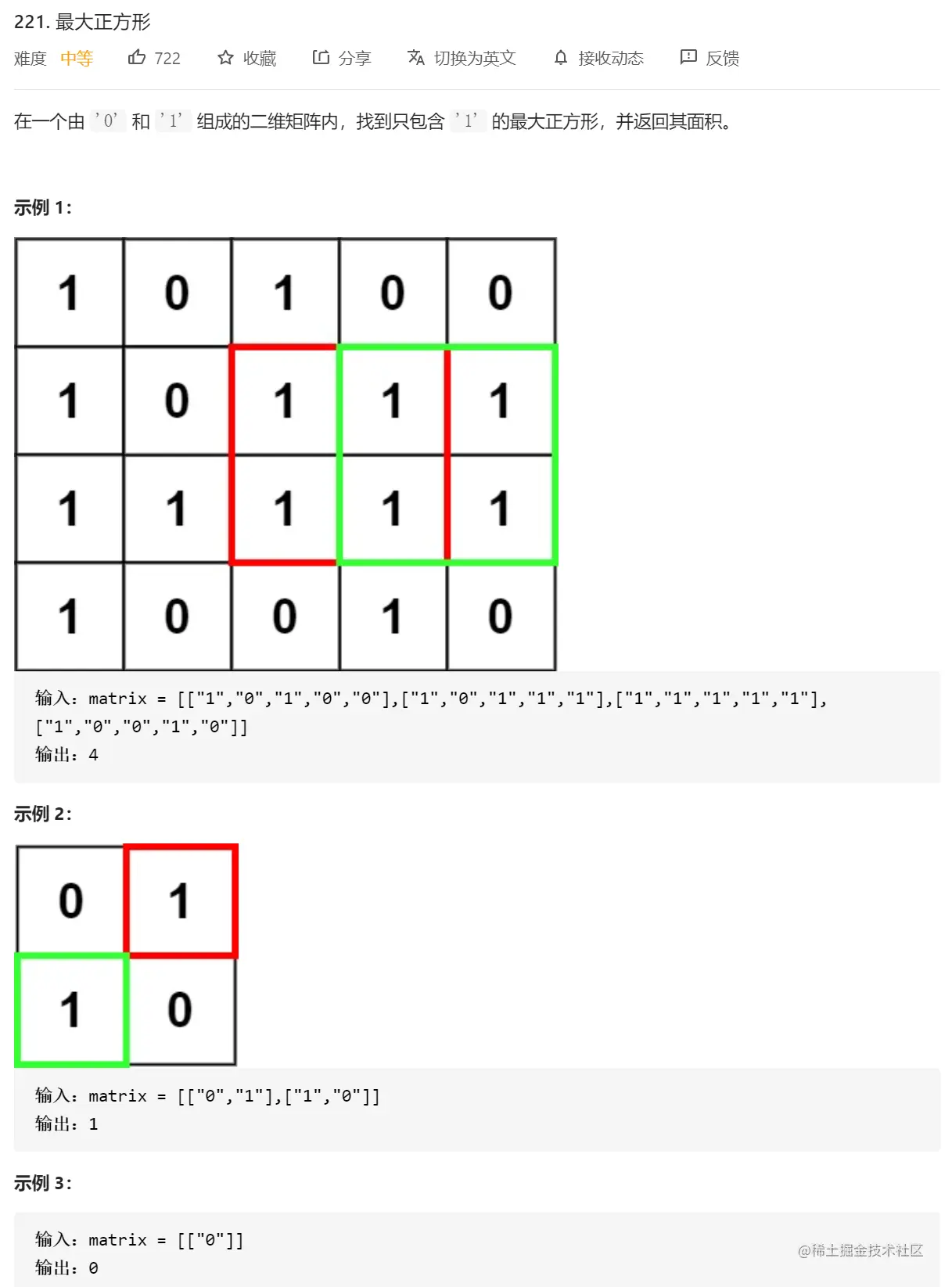
题目

思路：动态规划

• dp[i][j]表示以 (i, j) 为右下角，且只包含1的正方形的边长最大值
• 如果该位置的值是0，则dp=0,因为当前位置不可能在由1组成的正方形中；
• 如果该位置的值是1，则dp的值由其上方、左方和左上方的三个相邻位置的dp值决定。具体而言，当前位置的元素值等于三个相邻位置的元素中的最小值加1
• 转移方程：dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1])) + 1

代码

• 找三个数中min的方法: Math.min(num1, Math.min(num2, num3)

class Solution {
    public int maximalSquare(char[][] matrix) {
        int max = 0;
        int n = matrix[0].length, m = matrix.length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {//上、左边缘上的1
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = 1 + Math.min(dp[i - 1][j], Math.min(dp[i][j - 1], dp[i - 1][j - 1]));//三个数求min
                    }
                    max = Math.max(max, dp[i][j]);//注意位置
                } 
            }
        }
        return max * max;
    }
}