1，归并排序的思想

采用经典的分治法，先将数组进行拆分成小的数组，再按照左右两边的小数组顺序合并，再将剩余的顺序拷贝，最终再将临时的数组拷贝回原始数组中去

2，归并排序示意图

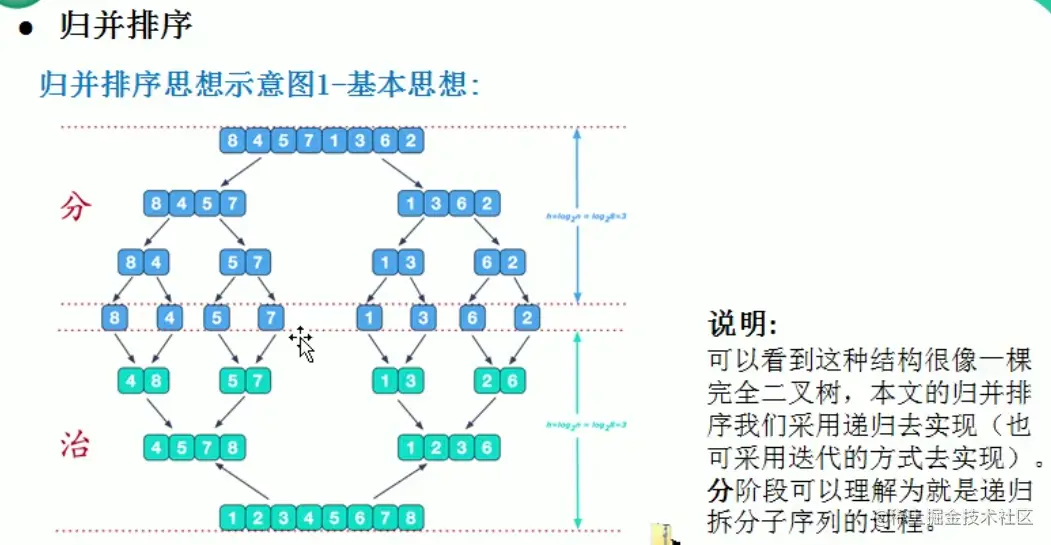
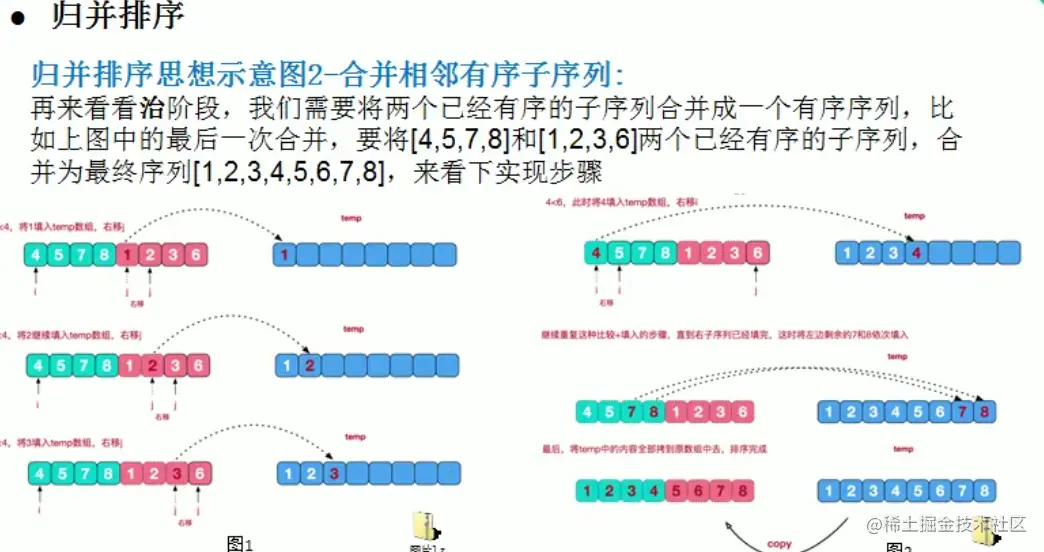
3，归并排序代码

 * 将数组拆分，也就是分
 * @param array
 * @param left
 * @param right
 * @param temp
 */
public static void mergeSort(int[] array, int left, int right, int[] temp) {
    if (left < right) {
        int middle = (left + right) / 2;
        //左递归分解
        mergeSort(array, left, middle, temp);
        //右递归分解
        mergeSort(array, middle + 1, right, temp);
        //合并
        merge(array, left, right, temp);
    }
}

/** 归并代码，也就是治
 * @param array  待排序的数组
 * @param left   左索引
 * @param middle 中间值
 * @param right  右索引
 * @param temp   临时数组
 */
public static void merge(int[] array, int left, int right, int[] temp) {
    int mid = (left + right) / 2;
    int i = left;
    int j = mid + 1;
    //指向临时数组的索引
    int t = 0;
    //第一步：先将左右两边的数组按照有序的顺序填充到temp数组中
    while (i <= mid && j <= right) {
        if (array[i] < array[j]) {
            temp[t] = array[i];
            i++;
            t++;
        } else {
            temp[t] = array[j];
            j++;
            t++;
        }
    }
    //第二步：将左右两边数组中剩余的数据依次填充到temp数组中
    while (i <= mid) {
        temp[t] = array[i];
        i++;
        t++;
    }
    while (j <= right) {
        temp[t] = array[j];
        j++;
        t++;
    }
    //第三步：最后进行数组的归并,并不是每次都拷贝所有的数据
    t = 0;
    int index = left;
    while (index <= right) {
        array[index] = temp[t];
        t++;
        index++;
    }
}