主成分分析PCA

1. 基本思想

有的时候，我们拿到的数据，多个维度之间的信息可能互相影响，导致单个维度的数据不是独立的，出现数据冗余。

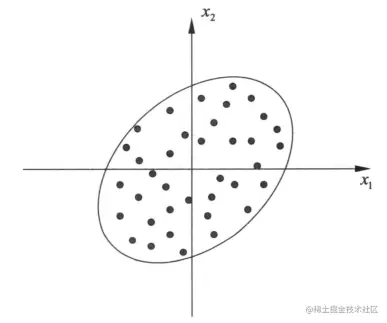
图1.1 数据线性相关

上图中， $x_{1},x_{2}$ 为线性相关，即 $x_{1}$ 确定时， $x_{2}$ 不是随机分布的。就好比一个人的身高和体重，两维数据存在互相影响。这时候我们希望==通过原基向量线性组合组成新的基向量，将数据以新基向量表示，从而使信息集中在前 $K$ 维度上，达到降维的目的==。

主成分分析对数据进行正交变换，几何上来看，即对数据轴进行旋转变换，并将数据以新坐标轴为基准表示。

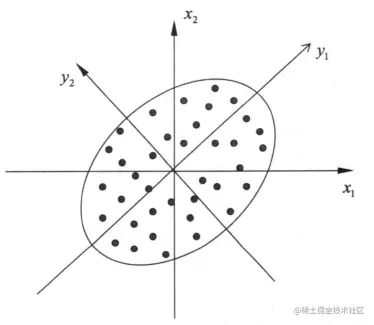
图1.2 主成分分析示意图

通过旋转坐标轴，数据中的变量 $y_{1},y_{2}$ 可以说是线性无关的，消除了数据冗余，直觉上讲我们认为信息集中在 $y_{1}$ 维上，以数据在 $y_{1}$ 上的投影代替原数据进行数据分析，达到降维的目的。

所以目前来讲，可以将问题分为两步：

数据表示和基变换
最优基向量选择

2. 数据表示和基变换

2.1 矩阵乘法

矩阵为线性方程组提供了一种表示方法

\left\{\begin{matrix}k_{11}x_{1} + k_{12}x_{2} = y_{1} \\k_{21}x_{1} + k_{22}x_{2} = y_{2}\end{matrix}\right.\\\begin{pmatrix}k_{11} & k_{12} \\k_{21} & k_{22}\end{pmatrix}\begin{pmatrix}x_{1} \\x_{2} \end{pmatrix}= \begin{pmatrix}y_{1} \\y_{2} \end{pmatrix}

这也是矩阵乘法“第一个矩阵的按行，第二个矩阵按列，顺序相乘相加”规则的由来。

2.2 数据表示与基向量表示

按照习惯以行向量的形式表示一个基向量，如：

p_{1} = \begin{pmatrix}p_{11} & p_{2} & p_{3} \end{pmatrix}

数据通常是以记录形式存在的，如：

{ "身高": 180, "体重":180, "年龄": 18 }

按照习惯以列向量的形式表示一个数据，如：

a_{1} = \begin{pmatrix} a_{11} \\ a_{12} \\ a_{13} \end{pmatrix}

同时为了简化后面的方差计算，通常先对数据进行去均值化，

a_{1} = \begin{pmatrix} a_{11} - \bar{a}_{1} \\ a_{12}- \bar{a}_{1} \\ a_{13}- \bar{a}_{1} \end{pmatrix}

我们之后说的原始数据，即指数据去均值化之后的结果。

2.3 基变换

数据的表示与采用的基向量有关，如二维下设原始数据基向量为 $(1,0),(0,1)$ ，采用其他基向量时，由向量内积的重要性质： A与B的内积 = A到B的投影长度 × |B|。基向量模为1的情况下，原始数据与基向量相乘即得到数据变换后的坐标。如

\begin{pmatrix} \frac{1}{\sqrt{2} } & \frac{1}{\sqrt{2} } \\ - \frac{1}{\sqrt{2} } & \frac{1}{\sqrt{2} } \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} \frac{5}{\sqrt{2} } \\ - \frac{1}{\sqrt{2} } \end{pmatrix}

表示数据 $(3,2)$ 在基向量 $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}),(-\frac{1}{\sqrt{2} },\frac{1}{\sqrt{2} })$ 下新坐标为 $(\frac{5}{\sqrt{2}},- \frac{1}{\sqrt{2} })$

==用行向量 $p_{i}$ 表示一个基向量，列向量 $a_{i}$ 表示一个数据，对多组数据进行基变换可以用矩阵乘法统一表示==。

\begin{pmatrix} p_{1} \\ p_{2} \\ \vdots \\ p_{r} \end{pmatrix} \begin{pmatrix} a_{1} & a_{2} & \dots & a_{m} \end{pmatrix} = \begin{pmatrix} p_{1}a_{1} & p_{1}a_{2} & \dots & p_{1}a_{m} \\ p_{2}a_{1} & p_{2}a_{2} & \dots & p_{2}a_{m} \\ \vdots & \vdots & \ddots & \vdots \\ p_{r}a_{1} & p_{r}a_{2} & \dots & p_{r}a_{m} \\ \end{pmatrix}

新坐标即为：（注意 $p_{i}，a_{i}$ 都是矩阵）

\begin{pmatrix} p_{1}a_{1}\\ p_{2}a_{1}\\ \vdots\\ p_{r}a_{1}\\ \end{pmatrix} , \begin{pmatrix} p_{1}a_{2}\\ p_{2}a_{2}\\ \vdots\\ p_{r}a_{2}\\ \end{pmatrix} , \dots , \begin{pmatrix} p_{1}a_{m}\\ p_{2}a_{m}\\ \vdots\\ p_{r}a_{m}\\ \end{pmatrix}

现在我们找到了基变换时求得对应的数据表示的方法，下一步需要对基向量组 $p^{T} = (p_{1},p_{2},\dots,p_{r} )$ 进行评估，以便找到最优基向量组。

3. 基向量评估

我们希望用前 $K$ 维表示数据并保留信息，就需要前 $K$ 维的表示尽可能接近数据的原始表示。

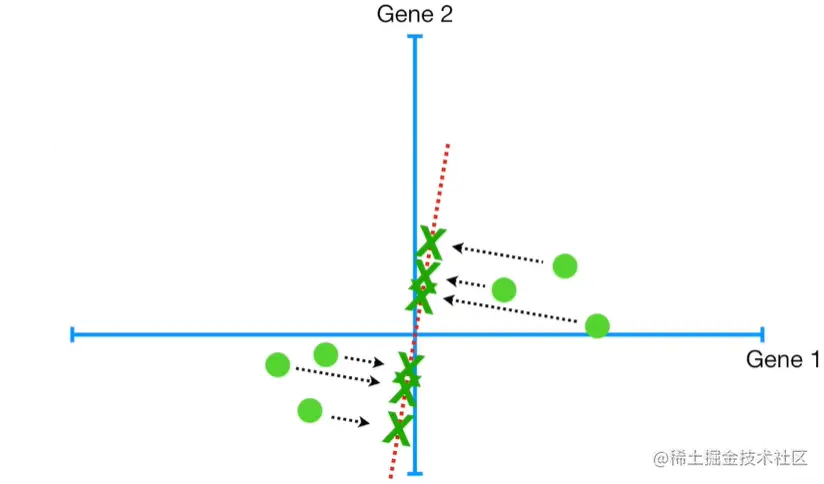
图3.1 数据表示

反映在图上，原点表示原数据（二维），叉号表示进行基变换并降维之后的数据（一维），我们希望叉号尽可能接近原点，同时也希望叉号尽可能分开，因为样本重叠同样带来数据冗余。

图3.2 数据表示

3.1 方差

由勾股定理，点到原点的距离是不变的（斜边不变），另两个直角边一个增加，另一个就减小，可以用叉号的分开程度，即其中一条直角边的长度衡量我们的基向量。所以我们以数据的方差和的均值（还记得我们对数据进行去均值化了吗）为标准，即对于第 $j$ 维，希望最大化

Var(a_{j}) =\frac{1}{m} \sum^{m}_{i=1} a_{ij}^{2}

其中 $a_{ij}$ 为进行基变换后的坐标。

3.2 协方差

我们用方差表示多组数据在一个维度上的分散程度和数据保留信息数，对于高维数据，我们用协方差表示数据维度与维度之间的相关性。为了使变量之间线性不想关，我们的目标是使 $Cov = 0$ ，即对于第 $x$ 维与第 $y$ 维，希望使下式等于 $0$

Cov(a_{x},a_{y}) = \frac{1}{m} \sum^{m}_{i=1} a_{xi}a_{yi}

其中 $a_{1},a_{2}$ 表示第1维，第2维。

3.3协方差矩阵

我们希望统一表示 $3.1,3.2$ 提出的优化目标，这个工具就是协方差矩阵。按照 $2.3$ 中数据矩阵的形式。对于 $m$ 个 $n$ 维数据

a_{i} = \begin{pmatrix} a_{i1} \\ a_{i2} \\ \vdots \\ a_{in} \end{pmatrix} , \\ X = (a_{1},a_{2}, \dots , a_{m}) , \\ \frac{1}{m}XX^{T} = \begin{pmatrix} Cov(1,1) & Cov(1,2) & \dots & Cov(1,n) \\ Cov(2,1) & Cov(2,2) & \dots & Cov(2,n) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(n,1) & Cov(n,2) & \dots & Cov(n,n) \\ \end{pmatrix}

例如3个2维数据

图3.3 协方差矩阵

利用协方差矩阵，现在的优化目标很明确了，我们需要使变换后的协方差矩阵除对角线外的元素全为0，并在对角线上将元素从大到小排列。

设==原始数据矩阵 $X$ 对应的协方差矩阵为 $C$ ==， $P$ 为一组基按行组成的矩阵，设 $Y = PX$ ，即 $Y$ 为 $X$ 对 $P$ 做基变换后的数据。设 $Y$ 的协方差矩阵为 $D$ ，有如下关系

D = \frac{1}{m} YY^{T} \\ \quad \quad \quad \quad = \frac{1}{m}(PX)(PX)^{T} \\ \quad \quad \quad = \frac{1}{m}PXX^{T}P^{T} \\ \quad \quad \quad \quad = P( \frac{1}{m}XX^{T})P^{T} \\ \quad = PCP^{T}

优化目标变成了==寻找一个矩阵 $P$ ，满足 $PCP^{T}$ 是一个对角矩阵，并且对角元素按从大到小依次排列，那么 $P$ 的前 $K$ 行就是要寻找的基，用 $P$ 的前 $K$ 行组成的矩阵乘以 $X$ 就使得 $X$ 从 $N$ 维降到了 $K$ 维并满足上述优化条件。==

由上文可知 $C$ 为 $n$ 行 $n$ 列的实对称矩阵，由线性代数，他可以找到 $n$ 个单位正交特征向量，设这 $n$ 个特征向量为 $e_{1},e_{2},\dots,e_{n}$ ，组成矩阵 $E = (e_{1},e_{2},\dots,e_{n})$ 。则

E^{T}CE =\Lambda = \begin{pmatrix} \lambda_{1} & & & \\ & \lambda _{2} & & \\ & & \ddots & \\ & & & \lambda _{n} \end{pmatrix}

其中 $\Lambda$ 为对角矩阵，其对角元素为各特征向量对应的特征值（可能有重复）。

到这里，我们发现我们已经找到了需要的矩阵 $P = E^{T}$ 。

$P$ 是协方差矩阵的特征向量单位化后按行排列出的矩阵，其中每一行都是 $C$ 的一个特征向量。如果设 $P$ 按照 $\Lambda$ 中特征值的从大到小，将特征向量从上到下排列，则用 $P$ 的前 $K$ 行组成的矩阵乘以原始数据矩阵 $X$ ，就得到了我们需要的降维后的数据矩阵 $Y$ 。