Resnets论文笔记

Jory
145 阅读4分钟

论文介绍

Resnets是2016年CVPR的最佳论文，其提出的架构在多个视觉任务上有优异的表现。解决了网络深度增加时梯度消失的问题，同时，训练时的收敛速度更快。并且，因为其提出的残差单元（Residual Unit）简单有效，其后被大量的CNN架构借鉴与采用。

本篇论文给出了不同残差块的统一形式，并从理论上分析了将identity mapping作为skip connections与after-addition activation优势（即信号可以在正向以及反向传播中，从一个单元传递到任意另一个单元），最后辅以实验证明。

论文内容

本节主要介绍Resnets提出的背景、所解决的问题以及其核心思想与具体内容。

问题

深度神经网络的深度以及参数量体现了模型的表达能力，网络的深度越深、参数量越多，模型的表达能力越强。但随着网络加深，梯度消失的问题就越严重，模型越难训练。结果就是更深的网络可能没有浅一些的网络效果好。

解决方法

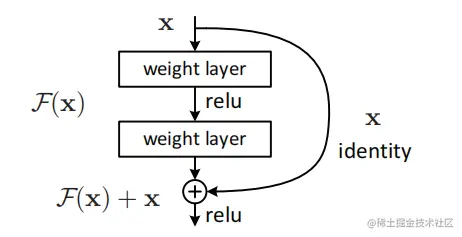
resnet2.png

Resnets通过学习残差的方式解决以上问题，其核心思想是给一个网络增加几层。若这些层学到的是identity mapping，其能力与之前的网络是一样的，不会变得更差。而通过卷积层学习identity mapping相对困难，若通过上图的网络结构学习残差F(x)\mathcal F(x)，则这几层的输出为F(x)+x\mathcal F(x)+x。而将卷积学习成输出为0（F(x)=0\mathcal F(x)=0）的映射，进而将F(x)+x\mathcal F(x)+x学习成identity mapping显然比通过卷积直接学习identity mapping更容易一些。

具体内容

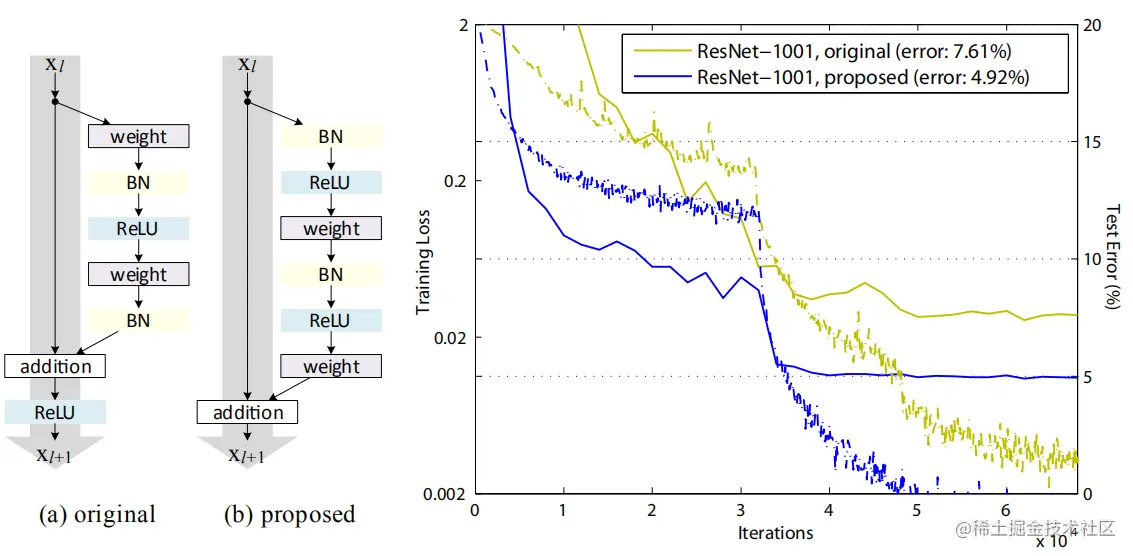resnet1.png Resnets中的残差单元如上图a、b所示，Resnets包含许多堆叠的残差单元，残差单元的结构有很多种，不同的残差单元都可以用下式表示：

yl=h(xl)+F(xl,Wl),(1)y_l=h(x_l)+\mathcal F(x_l, \mathcal W_l), \tag{1}
xl+1=f(yl).(2)x_{l+1} = f(y_l). \tag{2}

其中：xlx_l与xl+1x_{l+1}是第ll个残差单元的输入输出，F\mathcal F表示残差函数，Wl={Wl,k∣1≤k≤K}\mathcal W_l=\{W_{l,k}|_{1\le k\le K}\} 是第ll个残差单元中参数的集合，KK是残差块中包含的卷积层数。

若(1)(1)中h(xl)h(x_l)和(2)(2)中f(yl)f(y_l)都是identity mapping，则

xl+1=xl+F(xl,Wl).(3)x_{l+1}=x_l+\mathcal F(x_l, \mathcal W_l). \tag{3}

递归下去得到关于任何深层单元LL与任何浅层单元ll的关系：

xL=xl+∑i=lL−1F(xi,Wi).(4)x_L=x_l+\sum_{i=l}^{L-1}\mathcal F(x_i,\mathcal W_i). \tag{4}

从上式中可以看到两条性质：

  1. 任意深层的特征xLx_L都可以用任意浅层的特征xlx_l加上残差函数∑i=lL−1F\sum_{i=l}^{L-1}\mathcal F来表示。
  2. 任意深层的特征都可以看做之前的残差函数的和（加上x_0），而普通网络则是矩阵相乘。 同时，(4)(4)也具有良好的反向传播性质。用ε\varepsilon表示损失函数，计算梯度则得到：
∂ε∂xl=∂ε∂xL∂xL∂xl=∂ε∂xL(1+∂∂xl∑i=lL−1F(xi,Wi)).(5)\frac{\partial \varepsilon}{\partial x_l}=\frac{\partial\varepsilon}{\partial x_L}\frac{\partial x_L}{\partial x_l}=\frac{\partial\varepsilon}{\partial x_L}\left(1+\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\mathcal F(x_i, \mathcal W_i)\right). \tag{5}

公式(5)(5)表示梯度∂ε∂xl\frac{\partial\varepsilon}{\partial x_l}可以分为两部分：第一部分∂ε∂xL\frac{\partial\varepsilon}{\partial x_L}可以将信息不经过任何权重层传递给浅层；第二部分则经过权重层传递信息。并且由于在一个batch上所有sample的∂∂xl∑i=lL−1F\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\mathcal F的取值都是-1，所以解决了梯度消失的问题。

公式(4)(5)(4)(5)表明信息可以在正向和反向传播中从任意单元传递到另一单元。

Indentity Skip Connection的重要性（h(xl)=xlh(x_l)=x_l）

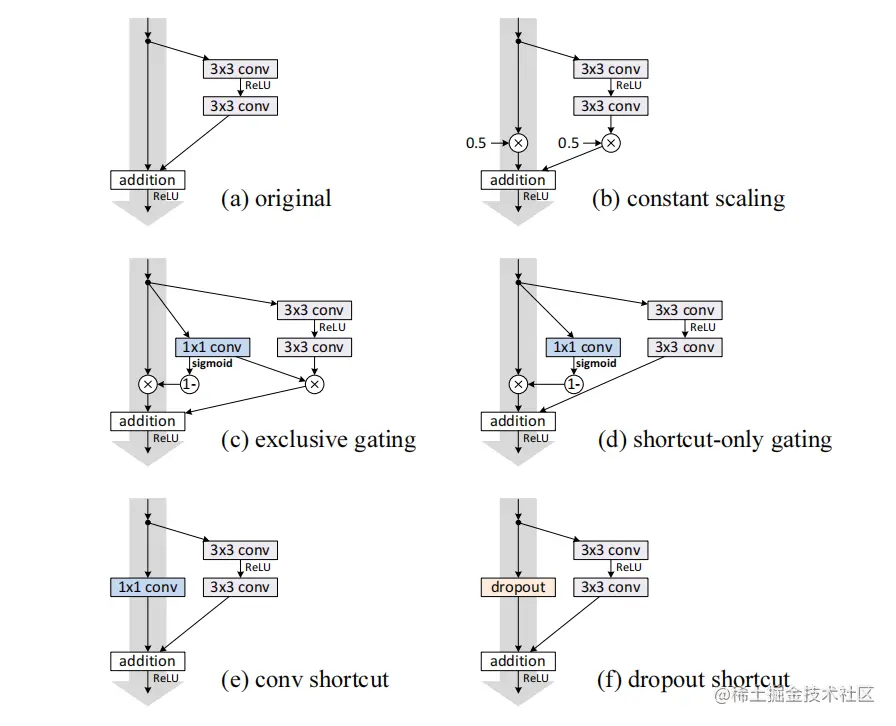resnet3.png 假设h(xl)=λlxlh(x_l)=\lambda_lx_l,则：

xl+1=λlxl+F(xl,Wl),x_{l+1}=\lambda_lx_l+\mathcal F(x_l,\mathcal W_l),

递归得到：

x_L=(\prod_{i=l}^{L-1}\lambda_i)x_l+\sum_{i=l}^{L-1}\hat\mathcal F(x_i,\mathcal W_i),

\hat\mathcal F已将λi\lambda_i乘入残差函数中，计算梯度得到：

\frac{\partial \varepsilon}{\partial x_l}=\frac{\partial\varepsilon}{\partial x_L}\frac{\partial x_L}{\partial x_l}=\frac{\partial\varepsilon}{\partial x_L}\left((\prod_{i=l}^{L-1}\lambda_i)+\frac{\partial}{\partial x_l}\sum_{i=l}^{L-1}\hat\mathcal F(x_i, \mathcal W_i)\right).

可以看出，若λi>1\lambda_i>1，前一项将成指数级放大，若λi<1\lambda_i<1，前一项将成指数级减小，接近0，这不利于反向传播信息，从而造成训练困难。若将h(xl)=λlxlh(x_l)=\lambda_lx_l换成更复杂的操作，那么梯度中的第一项将变为∏i=lL−1h′\prod_{i=l}^{L-1}h^{'}，也同样阻碍信息传播，造成训练困难。

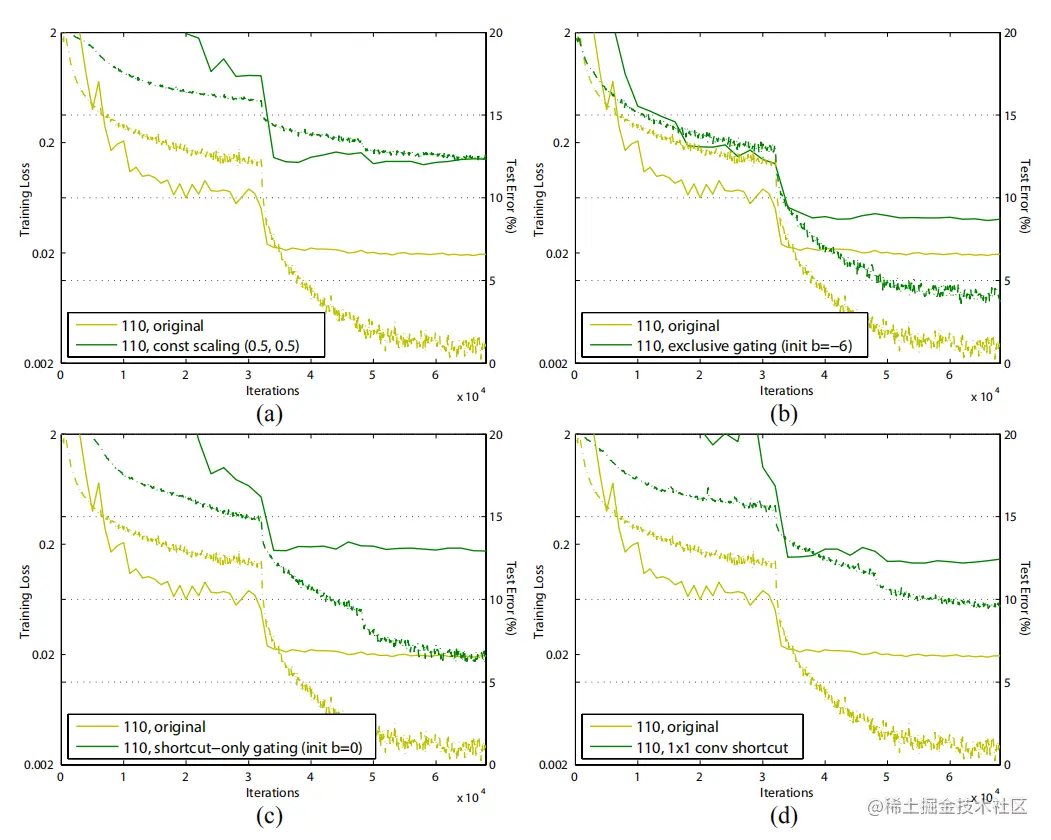resnet4.png 使用exclusive gating与1x1 conv比identity mapping有更多的参数，但表现却更糟，说明是优化问题影响了模型。

激活函数的使用（f(yl)f(y_l)）

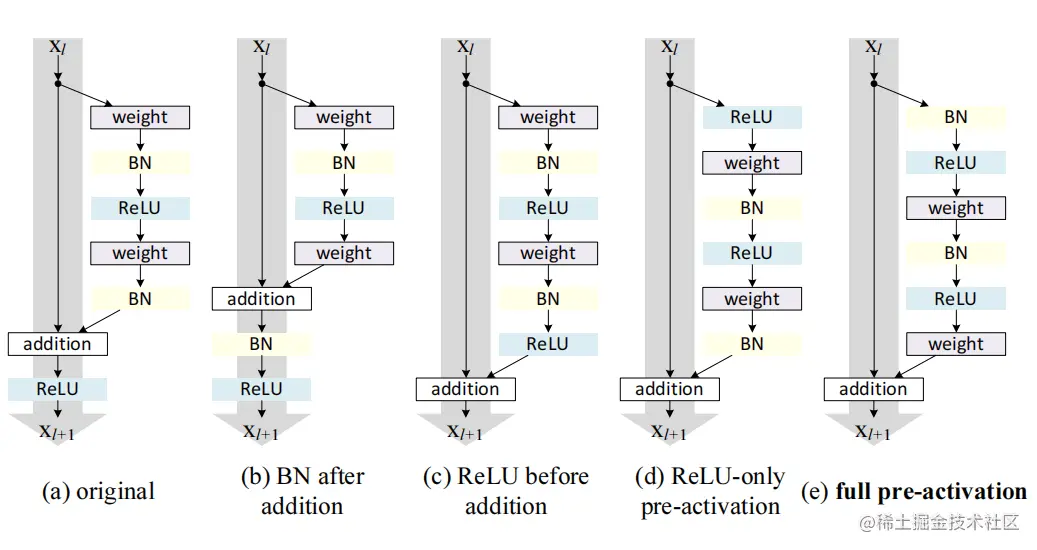resnet5.png BN after addition 影响信息的传播，造成训练困难。
ReLU before addition 此时F\mathcal F非负，前向传播时，信号单调递增，影响了模型的代表能力

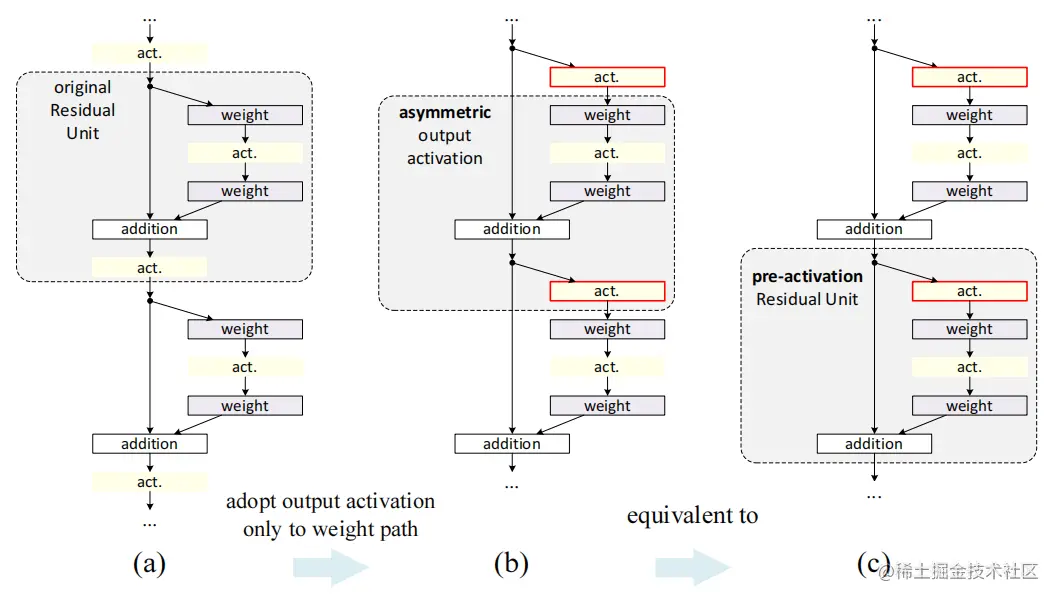resnet6.png 激活函数在addition之后会同时影响下一残差单元的两条路径，使用图(b)(b)的方式使其只影响一条路径，与公式(3)(3)对应。
ReLU-only pre-activation BN后，再addition，可能无法利用BN带来的优势。
full pre-activation 更容易训练；所有残差单元的输入都是归一化的，减少了过拟合。

avatar
文章
阅读
粉丝