动态规划
一. 什么是动态规划,我们要如何描述它?
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度, 因此它比回溯法、暴力法等要快许多。
现在让我们通过一个例子来了解一下DP的基本原理。
首先,我们要找到某个状态的最优解,然后在它的帮助下,找到下一个状态的最优解。
二.“状态”代表什么及如何找到它?
“状态”用来描述该问题的子问题的解。
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元? (表面上这道题可以用贪心算法,但贪心算法无法保证可以求出解,比如1元换成2元的时候)
首先我们思考一个问题,如何用最少的硬币凑够i元(i<11)?为什么要这么问呢?
两个原因:
- 当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。
- 这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题**(规模变小后的问题其实是原问题的子问题)。**
好了,让我们从最小的i开始吧。当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。
我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0, 表示凑够0元最小需要0个硬币。
当i=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的, 即d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。
当i=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。
当i=3时,我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元!5元太多了亲)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。
这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币, 我的目标就变成:凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是,我拿1个3元的硬币。
好了,这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够3元的。所以, 选择d(3)=1,怎么来的呢?具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:d(11),即凑够11元最少需要多少个硬币。 那状态转移方程是什么呢?既然我们用d(i)表示状态,那么状态转移方程自然包含d(i), 上文中包含状态d(i)的方程是:d(3)=min{d(3-1)+1, d(3-3)+1}。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,
import java.util.*;
/**
* @author SJ
* @date 2020/10/20
*/
public class Coins {
//**如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
public static void main(String[] args) {
int[] coins = {1, 3, 5};
System.out.println(poolMoneyByCoin(coins, 11));
poolMoneyByCoin2(coins, 11);
}
public static int poolMoneyByCoin(int[] coins, int money) {
int[] d = new int[money + 1];
d[0] = 0;
for (int i = 1; i <= money; i++) {
d[i] = i;
for (int j = 0; j < coins.length; j++) {
//如果拿coin[j]使当前的解比之前的更优的话
if (coins[j] <= i && d[i - coins[j]] + 1 < d[i])
d[i] = d[i - coins[j]] + 1;
}
}
return d[money];
}
//尝试输出方案
public static void poolMoneyByCoin2(int[] coins, int money) {
Map<Integer, List<Integer>> plan = new HashMap<>();
plan.put(0, new ArrayList<>());
// plan.get(0).add(0);
// int[] d = new int[money + 1];
// d[0] = 0;
for (int i = 1; i <= money; i++) {
plan.put(i, new ArrayList<>());
for (int k = 0; k < i; k++) {
plan.get(i).add(1);
}
for (int j = 0; j < coins.length; j++) {
//如果拿coin[j]使当前的解比之前的更优的话
if (coins[j] <= i && plan.get(i - coins[j]).size() + 1 < plan.get(i).size()) {
plan.get(i).clear();
plan.get(i).addAll(plan.get(i - coins[j]));
plan.get(i).add(coins[j]);
}
}
}
System.out.println("拿到的最小硬币的个数为" + plan.get(money).size() + " 此时的方案为:" + plan.get(money).toString());
}
}
结果:
"C:\Program Files\Java\jdk1.8.0_131\bin\java.exe"...
3
拿到的最小硬币的个数为3 此时的方案为:[5, 5, 1]
Process finished with exit code 0
我们要引入一个新词叫递推关系来将状态联系起来(说的还是状态转移方程)
一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。 (讲DP基本都会讲到的一个问题LIS:longest increasing subsequence)
正如上面我们讲的,面对这样一个问题,我们首先要定义一个“状态”来代表它的子问题, 并且找到它的解。注意,大部分情况下,某个状态只与它前面出现的状态有关, 而独立于后面的状态。
即从index=0开始逐一计算以arr[index]为最长递增序列终点的最长递增子序列长度,将其保存在dp[index]中,在计算后面任意一个index为终点的最长递增序列长度时,遍历前面的所有元素的maxLength,找出元素arr[i]<arr[index]的元素中的最大的maxLength值,将arr[index]加在这个序列上构成以arr[index]为终点的最长递增子序列,以此类推,当index到达结尾时所有子序列长度遍历结束,扫描整个数组dp[]里面的最大值就是最大递增子序列的长度(最后一个元素index并不一定是最长子序列的终点元素,即可能最长递增子序列 在一个序列的中间位置)
动态规划:
①创建动态规划数组保留每个计算结果,这里只需要一维数组dp[n];
②先计算dp[]中第一个位置的值,即dp[0],即以arr[0]为终点的最长递增子序列的最大子序列长度是1;
③从前往后计算dp[]中的每一个位置的值;注意递推关系的使用;
④扫描dp[],里面的最大值就是所求结果;
/**
* @author SJ
* @date 2020/10/20
*/
public class LIS {
//一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。
public static void main(String[] args) {
int[] nums = {1, 4, 2, 5, 3};
System.out.println(findLIS(nums, 5));
}
public static int findLIS(int[] nums, int n) {
int[] dp = new int[nums.length];
dp[0] = 1;
for (int i = 1; i < nums.length; i++) {
dp[i] = dp[i - 1];
for (int j = 0; j < i; j++) {
if (nums[j] <= nums[i] && dp[j] + 1 > dp[i])
dp[i] = dp[j] + 1;
}
}
return dp[n - 1];
}
}
"C:\Program Files\Java\jdk1.8.0_131\bin\java.exe"
3
Process finished with exit code 0
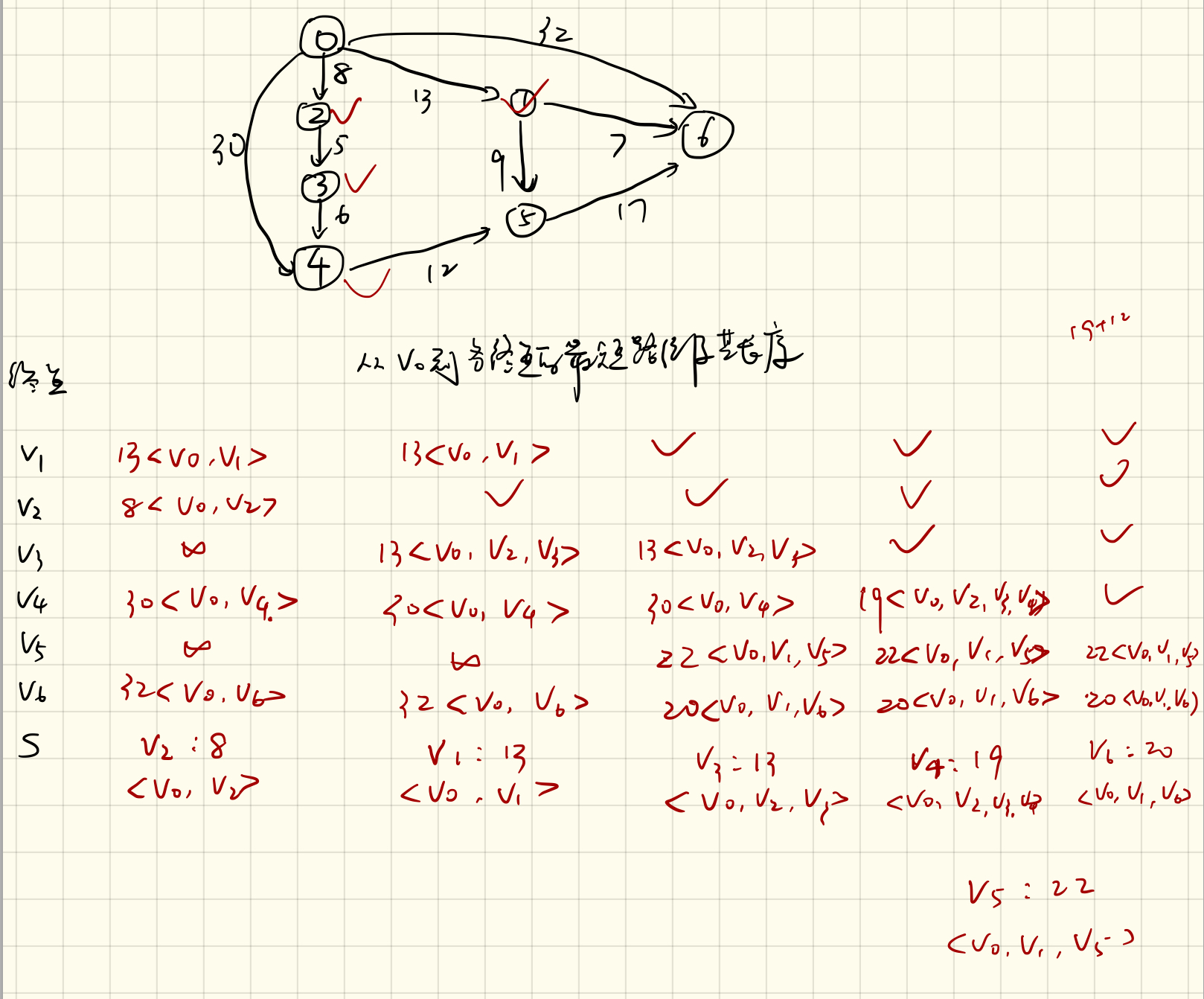
无向图G有N个结点(1<N<=1000)及一些边,每一条边上带有正的权重值。 找到结点1到结点N的最短路径,或者输出不存在这样的路径。
提示:在每一步中,对于那些没有计算过的结点, 及那些已经计算出从结点1到它的最短路径的结点,如果它们间有边, 则计算从结点1到未计算结点的最短路径。
import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;
/**
* @author SJ
* @date 2020/10/21
*/
public class NoPointGraph {
public static void main(String[] args) {
//邻接矩阵存入权值
int V = 6;
int[][] nums = new int[V + 1][V + 1];
getShortestPath(nums);
}
//从节点1到n的最短路径
public static void getShortestPath(int[][] adjacent) {
//初始化邻接矩阵存入最大值
for (int i = 0; i < adjacent.length; i++) {
for (int j = 0; j < adjacent[i].length; j++) {
adjacent[i][j] = Integer.MAX_VALUE;
}
}
//输入边
// Scanner scanner = new Scanner(System.in);
// System.out.println("输入点数;");
// int V = scanner.nextInt();
int V = 6;
// System.out.println("输入边数");
int E = 9;
// int E = scanner.nextInt();
// System.out.println("输入两点和边的权值");
//将信息存入邻接矩阵,0行0列不存信息
// for (int i = 1; i <= E; i++) {
// int x = scanner.nextInt();
// int y = scanner.nextInt();
// int weight = scanner.nextInt();
// adjacent[x][y]=weight;
// adjacent[y][x]=weight;
// }
adjacent[1][2] = 1;
adjacent[2][1] = 1;
adjacent[1][3] = 12;
adjacent[3][1] = 12;
adjacent[2][3] = 9;
adjacent[3][2] = 9;
adjacent[2][4] = 3;
adjacent[4][2] = 3;
adjacent[3][5] = 5;
adjacent[5][3] = 5;
adjacent[4][3] = 4;
adjacent[3][4] = 4;
adjacent[4][5] = 13;
adjacent[5][4] = 15;
adjacent[4][6] = 15;
adjacent[6][4] = 15;
adjacent[5][6] = 4;
adjacent[6][5] = 4;
//定义两个集合,存入未访问节点和已经访问的节点
Set<Integer> visited = new HashSet<>(V);//已经确定了最优解的点
Set<Integer> unVisited = new HashSet<>(V);////还没有找到最优解的点
//存局部最优解
int[] dp = new int[V + 1];
//初始化局部最优解
for (int i = 1; i <= V; i++) {
unVisited.add(i);
dp[i] = Integer.MAX_VALUE;
}
dp[1] = 0;
visited.add(1);
unVisited.remove(1);
//1.判断哪些已经访问过的数据m与i有边相连,如果有,计算dp[m]+adjcent[m][i]的最小值存入dp[i]
int currentIndex = 1;
while (unVisited.size() != 0) {
int tempMin = Integer.MAX_VALUE;//寻找currentIndex与i的最短路径
int tempMinIndex = -1;//记录current与i距离最小值时i的下标(就是说current与i点距离最近)
for (Integer i : unVisited) {
//如果当前节点与i有边相连
if (adjacent[currentIndex][i] != Integer.MAX_VALUE) {
//不断更新最短路径
if (dp[currentIndex] + adjacent[currentIndex][i] < dp[i])
dp[i] = dp[currentIndex] + adjacent[currentIndex][i];
}
if (dp[i] < tempMin) {
tempMin = dp[i];
tempMinIndex = i;
}
}
visited.add(tempMinIndex);
unVisited.remove(tempMinIndex);
currentIndex = tempMinIndex;
}
System.out.println(Arrays.toString(dp));
}
}
"C:\Program Files\Java\jdk1.8.0_131\bin\java.exe"...
[0, 0, 1, 8, 4, 13, 17]
Process finished with exit code 0
以上时求单源最短路径的Dijkstra算法:
1.adjcent[ ][ ]邻接矩阵存储对应点的权值([i,j]与[j,i]都要存)
2.visited集合:存储已经确定的找到了最短路径的点(这里要注意一下,不是访问过的点,而是已经找到了最短路径的点)
3.unvisited集合:存储还未找到最短路径的点
4.dp数组,存储子问题的最优解
dp[1]=0; (以上程序是从下标1开始算的)
过程:先将邻接矩阵的每个值和dp数组中每个值初始化为无穷大,这里用Interger.MAX_VALUE来替代
将点1加入visited集合,将点2-5加入unvisited集合
定义三个临时变量:
- currentIndex:上一回和找到的最优解的子问题的点,通过这一点找下一个最优解。
- tempMin:当前currentIndex与与他直接相连的点之间的最短距离
- tempMinIndex:与currentIndex有着最短距离的点
当unvisited集合长度不为0时,执行以下步骤:
遍历unvisited集合,记此时遍历的点为i
-
在unvisited中搜索与currentIndex直接相连的点x(此时currentIndex已经找到了最优解并保存在dp数组中)
并更新dp数组中dp[x]的值,比当前的dp[x]小的话就更新(判断(dp[currentIndex]+adjcent[currentIndex][x] 与dp【x】的大小)
在这个过程中找到最小的dp[i],即未确定最优解的点中最短的路径,将该点记为tempMinIndex,最短距离记为tempMin;
-
完成上述步骤后就已经找到了tempMinIndex的最优解,将tempMinIndex写入visited集合并从unvisited集合移除。更新currentIndex为tempMinIndex。
-
继续从步骤一开始执行直到不满足循环条件。
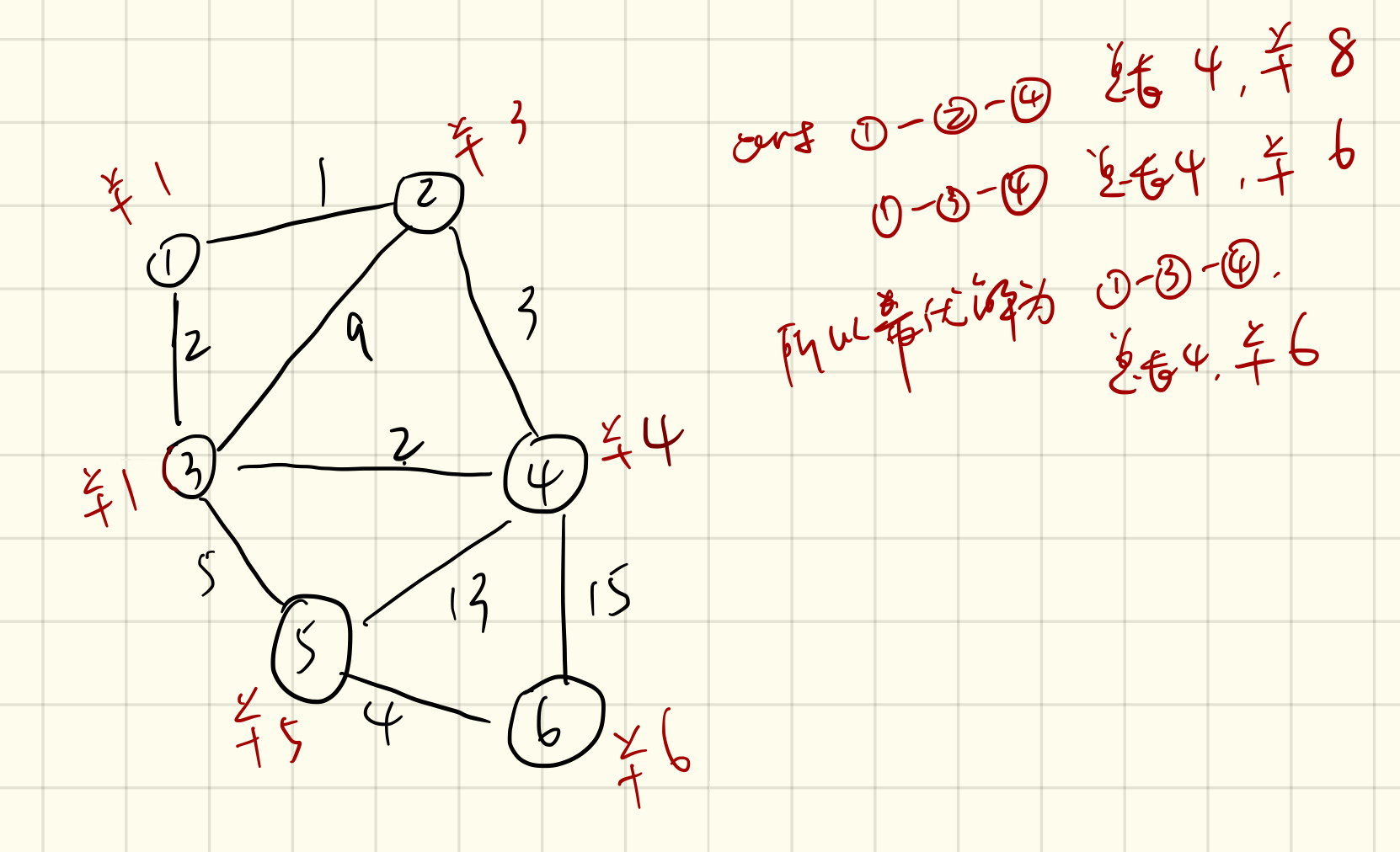
平面上有N*M个格子,每个格子中放着一定数量的苹果。你从左上角的格子开始, 每一步只能向下走或是向右走,每次走到一个格子上就把格子里的苹果收集起来, 这样下去,你最多能收集到多少个苹果。
解这个问题与解其它的DP问题几乎没有什么两样。第一步找到问题的“状态”, 第二步找到“状态转移方程”,然后基本上问题就解决了。
首先,我们要找到这个问题中的“状态”是什么?我们必须注意到的一点是, 到达一个格子的方式最多只有两种:从左边来的(除了第一列)和从上边来的(除了第一行)。 因此为了求出到达当前格子后最多能收集到多少个苹果, 我们就要先去考察那些能到达当前这个格子的格子,到达它们最多能收集到多少个苹果。 (是不是有点绕,但这句话的本质其实是DP的关键:欲求问题的解,先要去求子问题的解)
状态S[i][j]表示我们走到(i, j)这个格子时,最多能收集到多少个苹果。那么, 状态转移方程如下:
s[i][j]=A[i][j]+Max{s[i-1][j],if i>0,s[i][j-1] if j>0}, 其中A[i][j]是(i,j)这个点苹果的数量
S[i][j]有两种计算方式:1.对于每一行,从左向右计算,然后从上到下逐行处理;2. 对于每一列,从上到下计算,然后从左向右逐列处理。 这样做的目的是为了在计算S[i][j]时,S[i-1][j]和S[i][j-1]都已经计算出来了。
import java.util.Arrays;
/**
* @author SJ
* @date 2020/10/21
*/
public class PickUpApples {
public static void main(String[] args) {
pickUpApples(3, 3);
}
public static void pickUpApples(int M, int N) {
int[][] apples;
apples = new int[][]{{1, 4, 4}, {5, 3, 2}, {3, 5, 1}};
int[][] dp = new int[M][N];
dp[0][0] = apples[0][0];
//初始化第一排和第一列
for (int i = 1; i < M; i++) {
dp[0][i] = dp[0][i - 1] + apples[0][i];
}
for (int i = 1; i < N; i++) {
dp[i][0] = dp[i - 1][0] + apples[0][i];
}
//转移方程
for (int i = 1; i < M; i++) {
for (int j = 1; j < N; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + apples[i][j];
}
}
for (int[] ints : dp) {
System.out.println(Arrays.toString(ints));
}
}
}
输出的dp数组:
"C:\Program Files\Java\jdk1.8.0_131\bin\java.exe"...
[1, 5, 9]
[5, 8, 11]
[9, 14, 15]
Process finished with exit code 0
带有额外条件的DP问题。
无向图G有N个结点,它的边上带有正的权重值。
你从结点1开始走,并且一开始的时候你身上带有M元钱。如果你经过结点i, 那么你就要花掉S[i]元(可以把这想象为收过路费)。如果你没有足够的钱, 就不能从那个结点经过。在这样的限制条件下,找到从结点1到结点N的最短路径。 或者输出该路径不存在。如果存在多条最短路径,那么输出花钱数量最少的那条。 限制:1<N<=100 ; 0<=M<=100 ; 对于每个i,0<=S[i]<=100;正如我们所看到的, 如果没有额外的限制条件(在结点处要收费,费用不足还不给过),那么, 这个问题就和经典的迪杰斯特拉问题一样了(找到两结点间的最短路径)。 在经典的迪杰斯特拉问题中, 我们使用一个一维数组来保存从开始结点到每个结点的最短路径的长度, 即M[i]表示从开始结点到结点i的最短路径的长度。然而在这个问题中, 我们还要保存我们身上剩余多少钱这个信息。因此,很自然的, 我们将一维数组扩展为二维数组。M[i][j]表示从开始结点到结点i的最短路径长度, 且剩余j元。通过这种方式,我们将这个问题规约到原始的路径寻找问题。 在每一步中,对于已经找到的最短路径,我们找到它所能到达的下一个未标记状态(i,j), 将它标记为已访问(之后不再访问这个结点),并且在能到达这个结点的各个最短路径中, 找到加上当前边权重值后最小值对应的路径,即为该结点的最短路径。 (写起来真是绕,建议画个图就会明了很多)。不断重复上面的步骤, 直到所有的结点都访问到为止(这里的访问并不是要求我们要经过它, 比如有个结点收费很高,你没有足够的钱去经过它,但你已经访问过它) 最后Min[N-1][j]中的最小值即是问题的答案(如果有多个最小值, 即有多条最短路径,那么选择j最大的那条路径,即,使你剩余钱数最多的最短路径)。
dp数组要存入最短路径和最小花费(剩多少钱)两个值,我
在最短路径相同的情况下,如果当前路径花费比他少(剩的钱比它多)则更新,每次选择下一个节点的时候也要判断一下钱够不够。
上面的代码加了点额外的判断条件:
import java.util.*;
/**
* @author SJ
* @date 2020/10/21
*/
public class ShortestPath2 {
public static void main(String[] args) {
/**
* 你从结点1开始走,并且一开始的时候你身上带有M元钱。如果你经过结点i,
* 那么你就要**花掉S[i]元(可以把这想象为收过路费)。如果你没有足够的钱, 就不能从那个结点经过。
* 在这样的限制条件下,找到从结点1到结点N的最短路径。 或者输出该路径不存在。如果存在多条最短路径
* ,那么输出花钱数量最少的那条。
*/
//假设有6个点,9条边
int[][] adjacent=new int[7][7];
//初始化邻接矩阵存入最大值
for (int i = 0; i < adjacent.length; i++) {
for (int j = 0; j < adjacent[i].length; j++) {
adjacent[i][j] = Integer.MAX_VALUE;
}
}
adjacent[1][2] = 1;
adjacent[2][1] = 1;
adjacent[1][3] = 2;
adjacent[3][1] = 2;
adjacent[2][3] = 9;
adjacent[3][2] = 9;
adjacent[2][4] = 3;
adjacent[4][2] = 3;
adjacent[3][5] = 5;
adjacent[5][3] = 5;
adjacent[4][3] = 2;
adjacent[3][4] = 2;
adjacent[4][5] = 13;
adjacent[5][4] = 15;
adjacent[4][6] = 15;
adjacent[6][4] = 15;
adjacent[5][6] = 4;
adjacent[6][5] = 4;
//总花费,从下标为1 开始
int[] cost={0,1,3,1,4,5,6};
getShortestPath(adjacent,cost,30);
}
//从节点1到n的最短路径
public static void getShortestPath(int[][] adjacent, int[] cost,int property) {
int V = adjacent.length-1;//点数,还是从下标为1开始算
//定义两个集合,存入未访问节点和已经访问的节点
Set<Integer> visited = new HashSet<>(V);//已经确定了最优解的点
Set<Integer> unVisited = new HashSet<>(V);////还没有找到最优解的点
//存局部最优解,dp[i][0]存最短路径,dp[i][1]存走完这段路还剩下多少钱
int[][] dp = new int[V + 1][2];
//初始化局部最优解
for (int i = 1; i <= V; i++) {
unVisited.add(i);
dp[i][0] = Integer.MAX_VALUE;
dp[i][1] = 0;
}
dp[1][0] = 0;
dp[1][1] = property-cost[1];
property-=cost[1];
visited.add(1);
unVisited.remove(1);
int currentIndex = 1;
while (unVisited.size() != 0) {
int tempMin = Integer.MAX_VALUE;//寻找currentIndex与i的最短路径
int tempMinIndex = -1;//记录current与i距离最小值时i的下标(就是说current与i点距离最近)
int tempNodeCost=Integer.MIN_VALUE;
for (Integer i : unVisited) {
//如果当前节点与i有边相连且剩下的钱够经过这个节点
if (adjacent[currentIndex][i] != Integer.MAX_VALUE&&property>=cost[currentIndex]) {
//不断更新最短路径 路径比它短直接更新
if (dp[currentIndex][0] + adjacent[currentIndex][i] < dp[i][0])
{dp[i][0] = dp[currentIndex][0] + adjacent[currentIndex][i];
dp[i][1]=dp[currentIndex][1]-cost[i];
}
//路径一样长,开销比它少就更新
else if (dp[currentIndex][0] + adjacent[currentIndex][i] == dp[i][0]&&dp[currentIndex][1]-cost[i]>dp[i][1])
{ dp[i][0] = dp[currentIndex][0] + adjacent[currentIndex][i];
dp[i][1]=dp[currentIndex][1]-cost[i];
}
}
//上面结束后,跟顶点currentindex相连的节点的值的dp值就更新完毕了,此时,从所有还未确定最优解的点中找到dp值最小
//的最为下一个节点更新
if (dp[i][0]<tempMin||(dp[i][0]==tempMin&&dp[i][1]>tempNodeCost)){
tempMin=dp[i][0];
tempMinIndex=i;
tempNodeCost=dp[i][1];
}
}
visited.add(tempMinIndex);
unVisited.remove(tempMinIndex);
currentIndex=tempMinIndex;
}
for (int[] ints : dp) {
System.out.println(Arrays.toString(ints));
}
}
}
"C:\Program Files\Java\jdk1.8.0_131\bin\java.exe"
[0, 0]
[0, 29]
[1, 26]
[2, 28]
[4, 24]
[7, 23]
[11, 17]
Process finished with exit code 0