673. 最长递增子序列的个数

思路

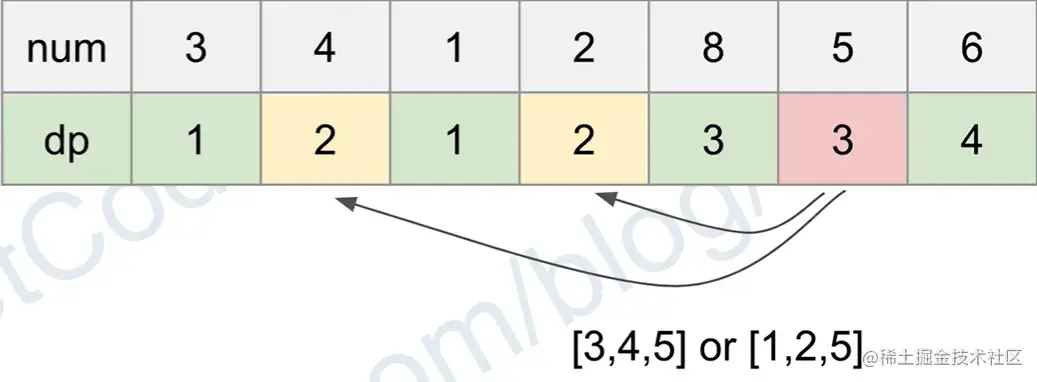
• dp，LC300一样的。
• dp[i]表示以nums[i]结尾的最长递增子序列的长度。
• count[i]表示长度为dp[i]的以nums[i]结尾的最长递增子序列有几个，因为来源可能有多个。如上图。

class Solution {
    public int findNumberOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        int[] count = new int[nums.length];
        int res = 0;// 一定初始化为0，（2，2，2，2，2
        int max = 0; //递增子序列的最大长度
        for (int i = 0; i < nums.length; i++) {
            dp[i] = 1;//注意初始化
            count[i] = 1;//注意初始化
            for (int j = 0; j < i; j++) {
                if (nums[j] < nums[i]) {
                    //在确定dp[i]时，dp[i]可能来源于多个相等的dp[j]
                    if (dp[j] + 1 > dp[i]) {
                        dp[i] = dp[j] + 1;//就不用再max了
                        count[i] = count[j];
                    } else if (dp[j] + 1 == dp[i]) {//相同的长度，表明有新的来源
                        count[i] = count[i] + count[j];
                    }
                    // dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            
            if (dp[i] > max) {//更新
                max = dp[i];
                res = count[i];
            } else if (dp[i] == max) //可能有多个相等的dp[i]都是最大值，累加
                res += count[i];
            }
            
        }
        return res;
    }
}