数据结构与算法-归并排序

1，归并排序

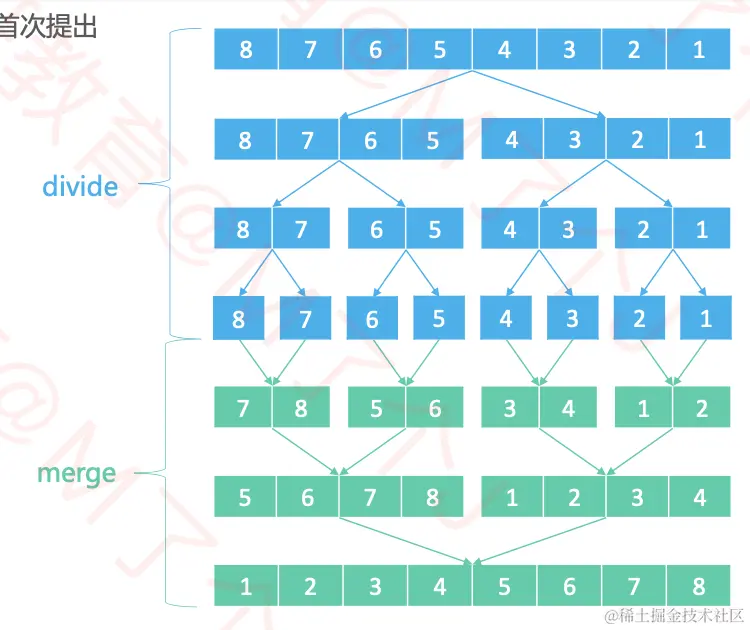
执行流程

1. 不断的将当前序列平均分割成2个子序列，知道不能再分割
2. 不断的将2个子序列合并成一个有序序列，直到最终只剩下1个有序序列

归并细节

• 需要merge的2组序列存在于同一个数组中，并且挨在一起

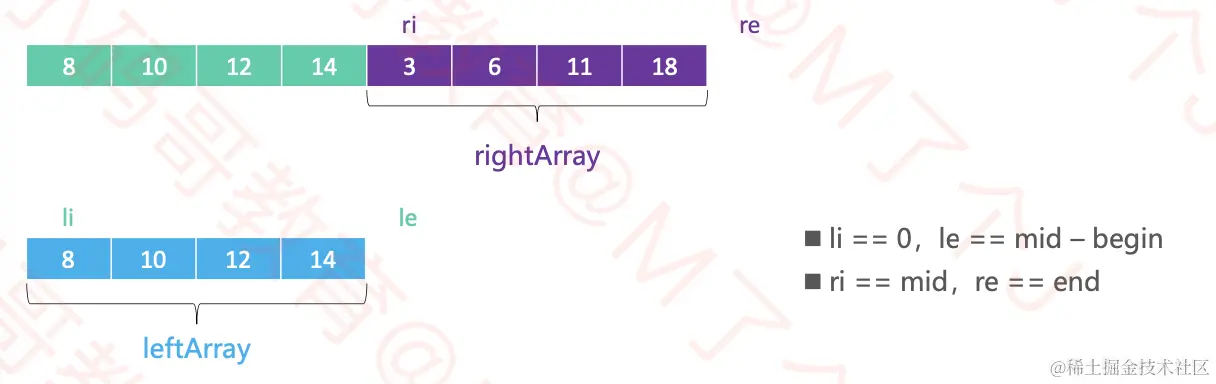
• 为了更好的完成merge，最好将其中1组序列备份出来，比如 [ begain, mid )
• 我们来确认几个标识，分为两个数组，左边的数组leftArray，右边的数组rightArray
• li 为leftArray的第一个索引，所以 li == 0
• le 为leftArray的最后一个索引，所以 le == mid - begain
• ri 为rightArray的第一个索引，所以 ri == mid
• re 为rightArray的最后一个索引，所以 re == end
• ai 为记录比较左边数组和右边数组元素比较的索引位置,存放比较小的元素的位置

归并排序实现

//准备一段临时的数组空间，备份左边的数组。空间大小为数组一半
leftArray = (T[]) new Object[array.length >> 1];
//从0到数组长度进行归并排序
sort(0,array.length);

//归并排序实现
private void sort(int begain, int end) {
    //只有一个数据，return
    if (end - begain < 2) return;
    //算出mid
    int mid = (begain + end) >> 1;
    //递归数组不断拆分
    sort(begain, mid);
    sort(mid, end);
    //合并拆分的元素
    merge(begain , mid , end);
}

//
private void merge(int begain, int mid, int end){
    //左边数组
    int li = 0, le = mid - begain;
    //右边数组
    int ri = mid, re = end;
    //比较array的索引
    int ai = begain;
    //备份数组的左边数组
    for (int i = li; i < le; i++){
        leftArray[i] = array[begain + i];
    }

    //li小于le说明数组比较结束
    while (li < le) {
        //
        if (ri < re && cpm(array[ri], leftArray[li]) < 0) {
            array[ai] = array[ri]; //拷贝右边数组到array
            ai++;
            ri++;
        } else {
            array[ai] = leftArray[li];//拷贝左边数组到array
            ai++;
            li++
        }
    }
}