曼哈顿距离总结（初级）

曼哈顿距离介绍

在平面内两点 $A(x_1, y_1$) 和 $B(x_2, y_2)$之间的曼哈顿距离为 $|x_1-x_2|+|y_1-y_2|$

借张图说明：

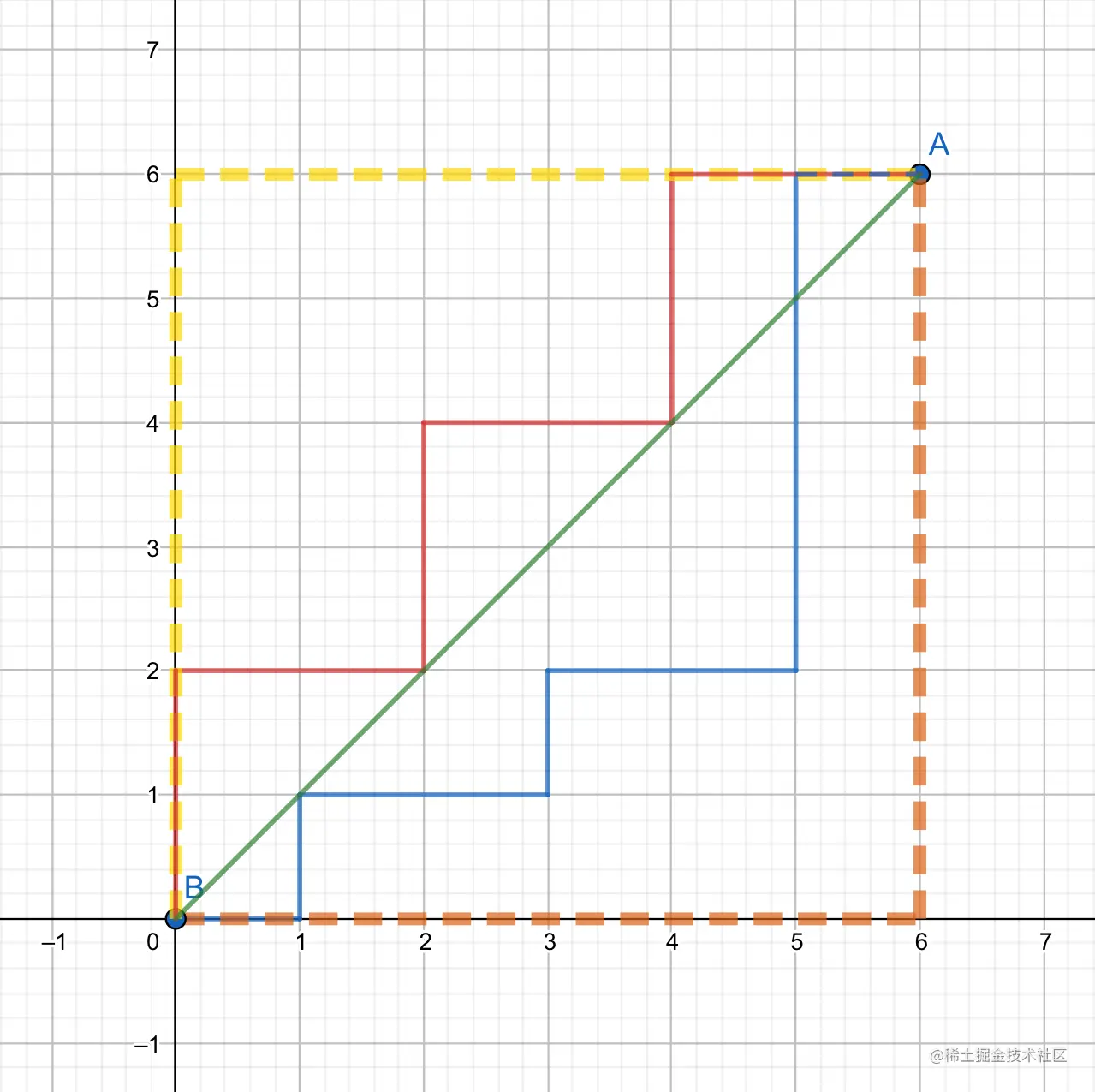
在 $A,B$ 间，黄线、橙线都表示曼哈顿距离，而红线、蓝线表示等价的曼哈顿距离

From: OI Wiki

求二维最大曼哈顿距离

问题描述

顾名思义，在二维平面上给你 $n$ 个点, 求曼哈顿距离最远的两个点之间的曼哈顿距离

解题思路

暴力做法

直接用两层for循环遍历所有的点对，求出他们的曼哈顿距离，同时维护一个最大值

正经的做法

假设我们要求点 $A(x_1,y_1)$ 和 $B(x_2,y_2)$ 之间的曼哈顿距离

我们可以先尝试对公式 $|x_1-x_2|+|y_1-y_2|$ 中的绝对值符号进行拆分：

$|x_1-x_2|+|y_1-y_2|=\begin{cases}x_1-x_2+y_1-y_2 & x_1>x_2, y_1>y_2 \\ x_1-x_2+y_2-y_1 & x_1>x_2, y_1<y_2 \\ x_2-x_1+y_1-y_2 & x_1<x_2, y_1>y_2 \\ x_2-x_1+y_2-y_1 & x_1<x_2, y_1<y_2\end{cases}$

整理得到：

$|x_1-x_2|+|y_1-y_2|=\begin{cases}(+x_1+y_1)-(+x_2+y_2) & x_1>x_2, y_1>y_2 \\ (+x_1-y_1)-(+x_2-y_2) & x_1>x_2, y_1<y_2 \\ (-x_1+y_1)-(-x_2+y_2) & x_1<x_2, y_1>y_2 \\ (-x_1-y_1)-(-x_2-y_2) & x_1<x_2, y_1<y_2\end{cases}$

我们发现：

1. 在展开绝对值的四种情况中，每一种都是 $X_1-X_2$ 的形式
2. 其中 $X_1$ 只与点 $A$ 有关， $X_2$ 只与点 $B$ 有关
3. $X_1$ 和 $X_2$ 中，$x$ 和 $y$ 的正负号相同
4. ==$X$ 的四种情况对应了 $x$ 和 $y$ 所有可能的符号的组合==

因此我们进行如下操作：

• 对每一个点，我们求出 $(x-y)$、$(x+y)$、$(-x+y)$、$(-x-y)$ ，分别存放在四个数组 $A$、$B$、$C$、$D$ 中
• 对于每一个数组，我们执行如下操作：
  • 求出它的最大值 $Max$ 和最小值 $Min$
  • 求出最大值与最小值的差 $Res = Max - Min$
• 求出所有 $Res$ 的最大值，即为答案：$Ans=max(A.Res,B.Res,C.Res,D.Res)$

这么做的意义是什么呢，我们逐步来分析

• 如果我们在上边求出的数组 $A$ 中任意取出两个点相减，则代表这两个点间一种可能曼哈顿距离的表达
• 如果我们在上一步中取出的恰好是 $A$ 的最大值和最小值，则代表如果所有的点都选择 $A$ 所代表的这种表达，最大的曼哈顿距离是多少
• 考虑到我们想要的是在所有可能的表达中，最大的曼哈顿距离，因此我们只需要对每一种表达取最大曼哈顿距离，再取他们中的最大值

如此我们就做完了

补充说明

不知道是否有人注意到，上述的思路其实存在一处模糊的地方：

• 在上边的过程中，我们考虑的是所有可能的表达，然而实际的曼哈顿距离只是其中的一种表达
  • 因为真正选择了两个点后，$x_1$ 和 $x_2$ 之间以及 $y_1$ 和 $y_2$ 之间的大小已经关系确定了，四种表达里实际只有一种是有效的

这就导致一个问题：

• 有没有可能，你通过上述方法选到的最大值采用的是 $A$ 表达，然而实际上这两个点的位置关系决定了它们应该采用 $B$ 表达，这个 $A$ 表达实际是无效的？

请读者自行思考几分钟：

好的，公布答案：

不可能的

我们从原式的角度来看：

$|x_1-x_2|+|y_1-y_2|=\begin{cases}x_1-x_2+y_1-y_2 & x_1>x_2, y_1>y_2 \\ x_1-x_2+y_2-y_1 & x_1>x_2, y_1<y_2 \\ x_2-x_1+y_1-y_2 & x_1<x_2, y_1>y_2 \\ x_2-x_1+y_2-y_1 & x_1<x_2, y_1<y_2\end{cases}$

1. 假设我们选择的两个点满足 $x_1>x_2, y_1>y_2$

2. 那么有效的表达是第一行对应的表达

3. 如果我们选择了第二行对应的表达(一个无效的表达)，那么：

   3.1 $|x_1-x_2|$ 对应的仍是 $x_1-x_2$，不变

   3.2 $|y_1-y_2|$ 对应的由 $y_1-y_2$ 变为了 $y_2-y_1$，变小了(原本是正数，现在是负数)

   3.3 因此总体得到的结果变小了

4. 同理可得，其他三种表达的结果也不如有效的表达大

5. 因此，有效的表达就是最大的表达

6. 而我们在上述算法中选择的是所有点的所有可能的表达中，最大的一个

7. 那它自然也是对应的两个点的四种表达中，最大的一个

8. 由第5步的结论，它就是有效的表达