变换(模型、视图、投影)

敏行
285 阅读4分钟

补充

对于旋转矩阵

Rθ=(cosθ−sinθsinθcosθ)R_{\theta} = \begin{pmatrix} cos_{\theta} & -sin_{\theta} \\ sin_{\theta} & cos_{\theta} \end{pmatrix}
R−θ=(cosθsinθ−sinθcosθ)=RθTR_{-\theta} = \begin{pmatrix} cos_{\theta} & sin_{\theta} \\ -sin_{\theta} & cos_{\theta} \end{pmatrix} = R^T_{\theta}
R−θ=Rθ−1R_{-\theta} = R^{-1}_{\theta}

如果一个矩阵的逆等于其转置，我们这个矩阵为正交矩阵。

3D变换

3维旋转矩阵有3个矩阵，分别绕x轴，y轴，z轴旋转。由于我们采用的是右手系，因此旋转是有定向的，正如在二维中，是x轴向y轴旋转，对应到3维中便是绕z轴旋转(x轴转向y轴)，绕x轴旋转(y转向z)，绕y轴旋转(z转向x)。

Rx(α)=(10000cosα−sinα00sinαcosα00001)R_x({\alpha}) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos_{\alpha} & -sin_{\alpha} & 0 \\ 0 & sin_{\alpha} & cos_{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

绕x轴旋转，故x不变，且y转向z

Ry(α)=(cosα0sinα00100−sinα0cosα00001)R_y({\alpha}) = \begin{pmatrix} cos_{\alpha} & 0 & sin_{\alpha} & 0 \\ 0 & 1 & 0 & 0 \\ -sin_{\alpha} & 0 & cos_{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

绕y轴旋转，故y不变，因为是z转向x，所以此处需要求逆

Rz(α)=(cosα−sinα00sinαcosα0000100001)R_z({\alpha}) = \begin{pmatrix} cos_{\alpha} & -sin_{\alpha} & 0 & 0 \\ sin_{\alpha} & cos_{\alpha} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

绕z轴旋转，故z不变，x转向y

绕任意轴旋转

绕任意轴旋转，首先将该轴旋转到任意的x, y, z轴上，然后可以应用基本的旋转矩阵，最后再逆旋转回来即可

R1RxR1T×(x,y,z)TR_1R_xR_1^T \times (x, y, z)^T

这里RxR_x的求法，从上面的解释可以得到，问题是如何求R1R_1，设想我们围绕旋转的轴为u，R1R_1便是将u转到x的矩阵。具体来说，这里需要以u为一轴，构造一个3维正交坐标系，然后将u-x对齐，其他两轴和y，z对齐。

构造如下，任取一t方向不与u重合。

w=t×uv=u×ww = t \times u \\ v = u \times w

此时，u, w, v便是我们构造出来的新坐标。注，这里是用叉乘。

如何将新坐标和原始坐标系重合呢？取R1=(u,w,v)R_1 = (u, w, v)，该旋转矩阵的含义便是将x, y, z旋转到u, w, v的旋转矩阵。因此

[xuxvxwyuyvywzuzvzw][1000cosα−sinα0sinαcosα][xuyuzuxvyvzvxwywzw]\begin{bmatrix} x_u & x_v & x_w \\ y_u & y_v & y_w \\ z_u & z_v & z_w \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos_{\alpha} & -sin_{\alpha} \\ 0 & sin_{\alpha} & cos_{\alpha} \end{bmatrix} \begin{bmatrix} x_u & y_u & z_u \\ x_v & y_v & z_v \\ x_w & y_w & z_w \end{bmatrix}

罗德里格旋转公式

引用 zhuanlan.zhihu.com/p/451579313

一个向量绕旋转轴旋转给定角度以后得到新向量的计算公式。

  • 叉乘矩阵
[xayaza]×[xbybzb]=[0−zayaza0−xa−yaxa0][xbybzb]\begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \times \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix} = \begin{bmatrix} 0 & -z_a & y_a \\ z_a & 0 & -x_a \\ -y_a & x_a & 0\end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix}
  • 向量三重积展开
a⃗×(b⃗×c⃗)=(a⃗⋅c⃗)b⃗−(a⃗⋅b⃗)c⃗\vec{a} \times (\vec{b} \times \vec{c}) = (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b})\vec{c}

1.PNG

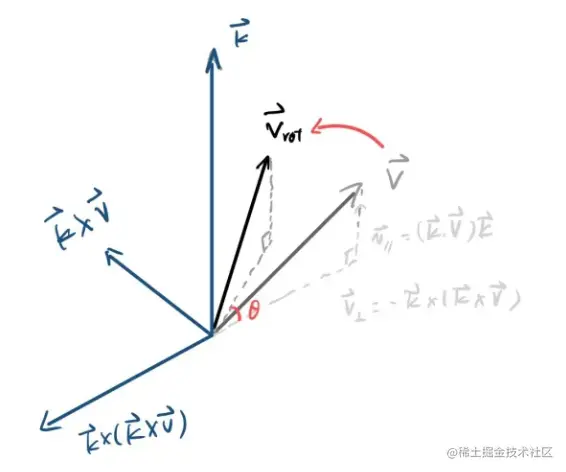
问题描述如下，已知 v⃗\vec{v} 是三维空间中一向量，k⃗\vec{k} 是与转轴同向的单位向量，θ\theta 是 v⃗\vec{v} 绕 k⃗\vec{k} 的右手(逆时针)方向旋转经过的角度，求旋转后向量 vrot⃗\vec{v_{rot}}。

将 v⃗\vec{v} 分为与 k⃗\vec{k} 垂直的分量 v⊥⃗\vec{v_{\perp}} 和平行的分量 v//⃗\vec{v_{\mathop{//}}}，有 v⃗=v⊥⃗+v//⃗\vec{v} = \vec{v_{\perp}} + \vec{v_{\mathop{//}}}。

v//⃗=(k⃗⋅v⃗)⋅k⃗\vec{v_{\mathop{//}}} = (\vec{k} \cdot \vec{v}) \cdot \vec{k}
v⊥⃗=v⃗−v//⃗=(k⃗⋅k⃗)⋅v⃗−(k⃗⋅v⃗)⋅k⃗=−k⃗×(k⃗×v⃗)\vec{v_{\perp}} = \vec{v} - \vec{v_{\mathop{//}}} = (\vec{k} \cdot \vec{k}) \cdot \vec{v} - (\vec{k} \cdot \vec{v}) \cdot \vec{k} = -\vec{k} \times (\vec{k} \times \vec{v})

从图中可以看出几何关系

vrot//⃗=v//⃗\vec{v_{rot\mathop{//}}} = \vec{v_{\mathop{//}}}

现在只要求出 vrot⊥⃗\vec{v_{rot\perp}} 就能求出 vrot⃗\vec{v_{rot}} 了。

由于∣∣vrot⊥⃗∣∣=∣∣v⊥⃗∣∣||\vec{v_{rot\perp}}|| = ||\vec{v_{\perp}}||，可以得到如下公式。

vrot⊥⃗=v⊥⃗∣∣v⊥⃗∣∣⋅∣∣v⊥⃗∣∣cos(θ)+k⃗×v⃗∣∣k⃗×v⃗∣∣⋅∣∣k⃗×v⃗∣∣sin(θ)\vec{v_{rot\perp}} = \frac{\vec{v_{\perp}}}{||\vec{v_{\perp}}||} \cdot ||\vec{v_{\perp}}|| cos(\theta) + \frac{\vec{k} \times \vec{v}}{||\vec{k} \times \vec{v}||} \cdot ||\vec{k} \times \vec{v}||sin(\theta)
vrot⊥⃗=v⊥⃗⋅cos(θ)+k⃗×v⃗⋅sin(θ)\vec{v_{rot{\perp}}} = \vec{v_\perp} \cdot cos(\theta) + \vec{k} \times \vec{v} \cdot sin(\theta)

注意这里 k⃗×v⃗\vec{k} \times \vec{v} 的标量和 v⊥⃗\vec{v_{\perp}} 是相等的。

综上可得

vrot⃗=vrot//⃗+vrot⊥⃗\vec{v_{rot}} = \vec{v_{rot\mathop{//}}} + \vec{v_{rot\perp}}
vrot⃗=v//⃗+v⊥⃗⋅cos(θ)+k⃗×v⃗⋅sin(θ)=v//⃗+(v⃗−v//⃗)⋅cos(θ)+k⃗×v⃗⋅sin(θ)=cos(θ)⋅v⃗+(1−cos(θ))⋅v//⃗+k⃗×v⃗⋅sin(θ)=cos(θ)⋅v⃗+(1−cos(θ))⋅(k⃗⋅v⃗)⋅k⃗+k⃗×v⃗⋅sin(θ)\vec{v_{rot}} = \vec{v_{\mathop{//}}} + \vec{v_{\perp}} \cdot cos(\theta) + \vec{k} \times \vec{v} \cdot sin(\theta) \\ = \vec{v_{\mathop{//}}} + (\vec{v} - \vec{v_{\mathop{//}}}) \cdot cos(\theta) + \vec{k} \times \vec{v} \cdot sin(\theta) \\ = cos(\theta) \cdot \vec{v} + (1 -cos(\theta)) \cdot \vec{v_{\mathop{//}}} + \vec{k} \times \vec{v} \cdot sin(\theta) \\ = cos(\theta) \cdot \vec{v} + (1 - cos(\theta)) \cdot (\vec{k} \cdot \vec{v}) \cdot \vec{k} + \vec{k} \times \vec{v} \cdot sin(\theta)

根据公式可得

vrot⃗=v⃗+(1−cos(θ))⋅k⃗×(k⃗×v⃗)+k⃗×v⃗⋅sin(θ)\vec{v_{rot}} = \vec{v} + (1 - cos(\theta)) \cdot \vec{k} \times (\vec{k} \times \vec{v}) + \vec{k} \times \vec{v} \cdot sin(\theta)
vrot⃗=v⃗+(1−cos(θ))⋅Rk2⋅v⃗+Rk⋅v⃗⋅sin(θ)=[I+(1−cos(θ))⋅Rk2+Rk⋅sin(θ)]⋅v⃗\vec{v_{rot}} = \vec{v} + (1 - cos(\theta)) \cdot R^2_k \cdot \vec{v} + R_k \cdot \vec{v} \cdot sin(\theta) \\ = [I + (1 - cos(\theta)) \cdot R^2_k + R_k \cdot sin(\theta)] \cdot \vec{v}
M=I+(1−cos(θ))⋅Rk2+Rk⋅sin(θ)vrot⃗=M⋅v⃗M = I + (1 - cos(\theta)) \cdot R^2_k + R_k \cdot sin(\theta) \\ \vec{v_{rot}} = M \cdot \vec{v}

视图变换(Viewing/Camera transformation)

什么是视图变换

用拍照来比喻一下：

  • 找一个好位置，安排模特(model transformation)
  • 找一个好的角度，摆放相机(view transformation)
  • 拍照! (projection transformation)

如何视图变换

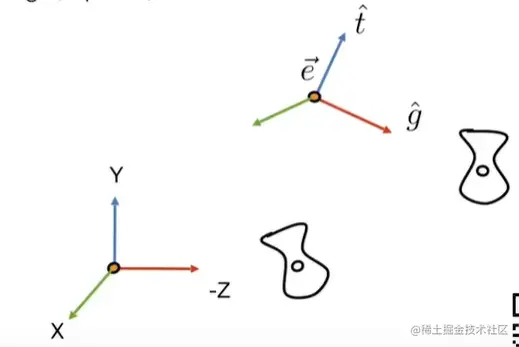
首先定义相机：

  • Position e⃗\vec{e}
  • Look-at / gaze direction g^\hat{g}
  • Up direction t^\hat{t}

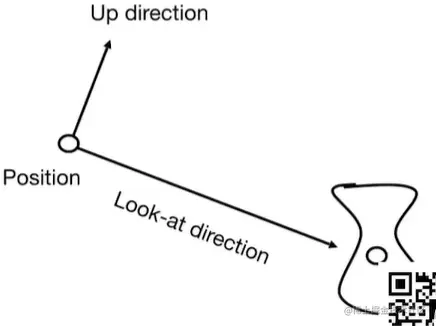
如果相机和物体一起变换，那么相对不变。

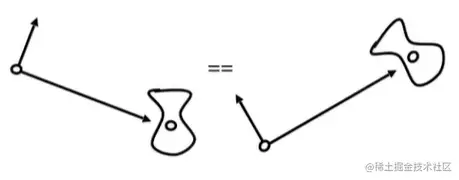
所以，我们规定将相机放在原点，up在Y轴，看向-z方向

这样做的原因是，以后有很多操作会非常方便。

那么如何求变换矩阵MviewM_{view}?

  • 将e平移到原点
  • 旋转g到-Z
  • 旋转t到Y
  • 旋转(g×t)(g \times t)到X

Mview=RviewTviewM_{view} = R_{view}T_{view}

首先

Tview=[100−xe010−ye001−ze0001]T_{view} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix}

旋转g到-Z，t到Y，g×tg \times t到X。 反向考虑一下，X到(g×t)(g \times t)，Y到t，Z到-g。

投影变换(Projection transformation)

  • 投影的目的是将3D映射为2D
  • 正交投影(orthographic projection)
  • 透视投影(perspective projection)

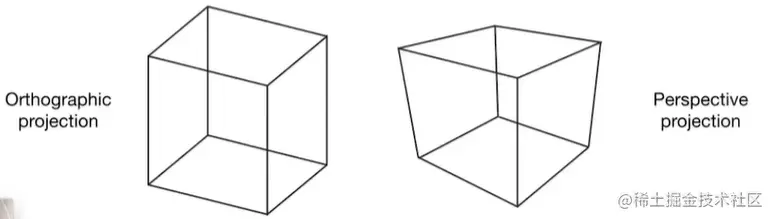
对于正交投影，3D中平行的线，投影之后还是平行。而透视投影则不是。

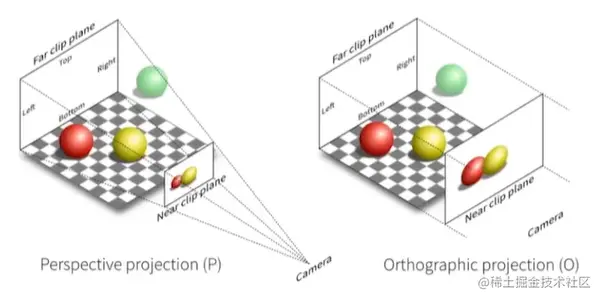
正交投影

  • 相机位于原点，朝向-Z，up位于Y
  • 丢弃Z轴
  • 平移并且缩放结果在一个矩形中[−1,1]2[-1, 1]^2

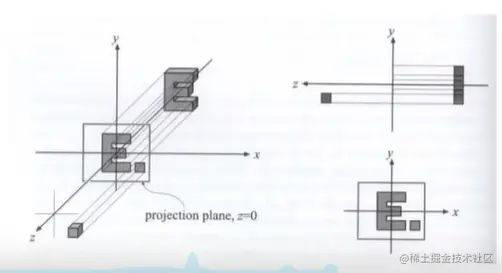
更常规得看，我们是将一个立方体[l,r]×[b,t]×[f,n][l, r] \times [b, t] \times [f, n]映射到一个(正则，规范、标准)的立方体[−1,1]3[-1, 1]^3

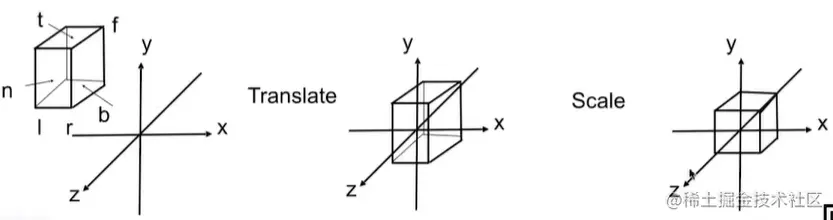
变换矩阵

先平移，再缩放

Mortho=[2r−l00002t−b00002n−f00001][100−r+l2010−t+b2001−n+f20001]M_{ortho} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix}

这里可能会有人有疑问，为什么要压缩到一个小立方体呢？其实是为了之后计算方便，在转换到屏幕坐标的时候就会重新拉伸回来，不必太纠结。

透视投影(Perspective Projection)

  • 在图形学中应用最广泛
  • 近大远小

在齐次坐标系中

  • (x, y, z, 1), (kx, ky, kz, k!=0), (xz, yz, z2z^2, z!=0)，在3D中都表示相同的点(x, y, z)
  • (1, 0, 0, 1)和(2, 0, 0, 2)都表示(1, 0, 0)

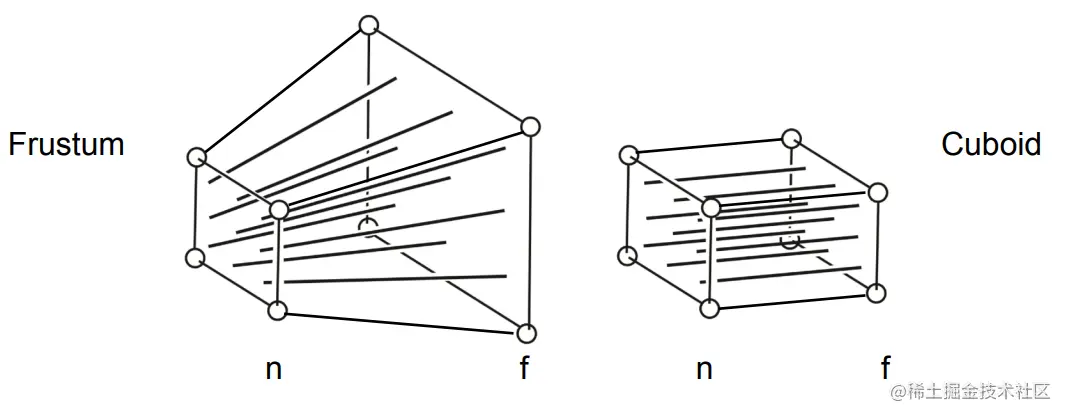
如何完成投影变换

  • 首先，把截锥压成一个长方体(n->n, f->f)(Mpersp−>orthoM_{persp->ortho})
  • 做正交投影(MorthoM_{ortho})

第一步的关键因素是，发现变换点(x′x^{'}, y′y^{'}, z′z^{'})和原始点(x, y, z)之间的关系

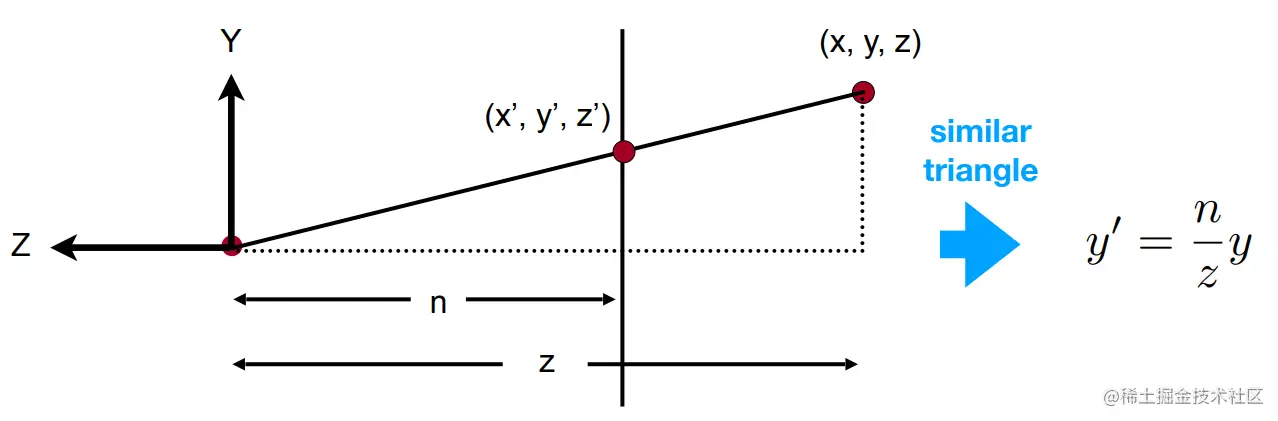
很明显，根据相似三角形公式，可以得到如下的结论：

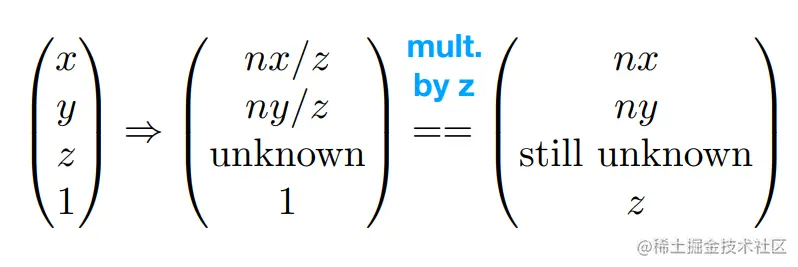
而由这个公式，我们可以推出以下矩阵：

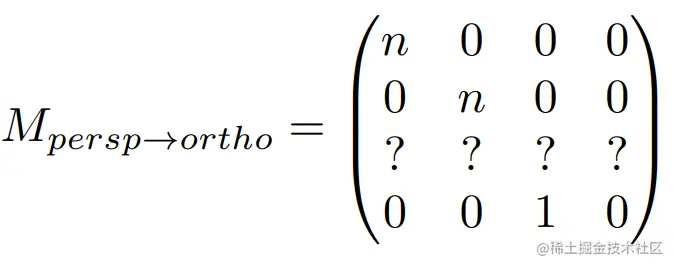
目前，我们还无法得知第三行是什么，不过，通过观察可以发现：

  1. 近平面中任何点是不会改变的

第三行必须是(0 0 A B)，其中A和B是未知的

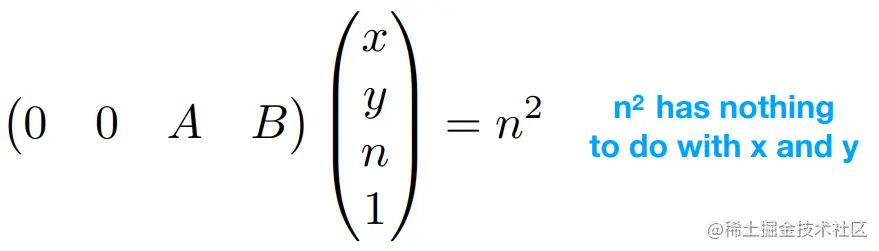
  1. 远平面中任何点的z值是不会改变的

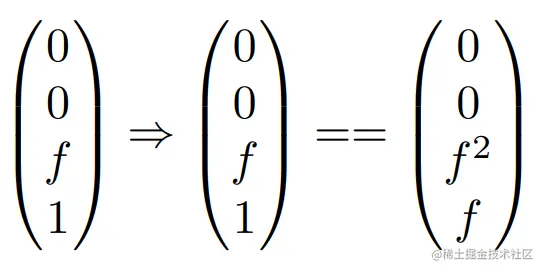
从上面，可以推出两个方程：

An+B=n2Af+B=f2An + B = n^2 \\ Af + B = f^2

解得：

A=n+fB=−nfA = n + f \\ B = -nf

最后

Mpersp=MorthoMpersp−>orthoM_{persp} = M_{ortho}M_{persp->ortho}

闫令琪 <<现代计算机图形学>>，blog.csdn.net/qq_38065509…

avatar
文章
阅读
粉丝