本文想给大家分享的是《A Univariate Bound of Area Under ROC》论文。
本文首发于公众号“码农修炼厂”,热衷于机器学习、推荐系统、数据挖掘、深度学习论文和技术的分享,欢迎关注!
还是那句话水平有限,大家多多包涵,非常欢迎任何形式的讨论,大家共同学习共同进步。码字不易,喜欢就请大家点赞、收藏、转发三连吧!
蟹蟹大家的支持,欢迎大家关注,转发,分享三连!
需要下载原论文的,可以关注公众号,后台回复“UBAUC”,下载论文!
Abstract & Intro
ROC下面积(AUC)是二元分类和二部排序问题的一个重要指标。然而,很难将AUC作为直接优化的学习目标(0-1损失是离散的),所以现有的大多数算法都是基于对AUC的替代损失进行优化。替代损失的一个重大缺点就是他们需要对训练数据的成对比较,这导致运行时间慢,并且增加了用于在线学习的本地存储。 本文提出了一个基于AUC risk的新的替代损失,它并不需要成对比较,但仍然可以对预测进行排序。作者进一步证明了,排序操作可以被避免,并且基于该代理项得到的学习目标在时间和存储上都具有线性复杂度。 最后,实验验证了基于代理损失的AUC优化在线算法和批处理算法的有效性。
Problem Definition
{(xi,yi)}i=1N,为样本,yi∈{−1,+1}为标签, xi∈Rd.I+={i∣yi=+1},I−={i∣yi=−1}分别为正样本和负样本的下标,其中N+=∣I+∣,N−=∣I−∣,N++N−=N。定义一个指示函数I:Ia=1,为真返回1,为假返回0。
二元分类器:cw,θ:Rd↦{−1,+1}:
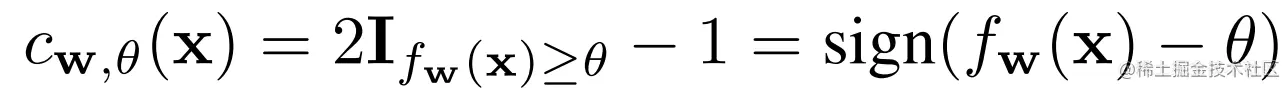
fw:Rd↦R,w为参数,θ为预测的阈值。
令ci=fw(xi)为第i个样本的预测分数,并假设预测的分数都没有完全相等的。
对于阈值θ,预测值大于该阈值的负样本为false positive,计算如下: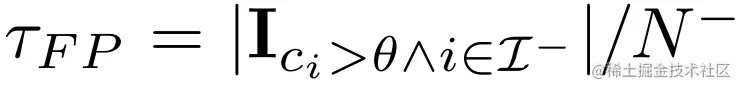 同样的,正样本阈值高于θ的为true positive,计算如下:
同样的,正样本阈值高于θ的为true positive,计算如下: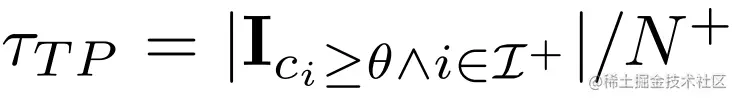 AUC risk定义如下:
AUC risk定义如下: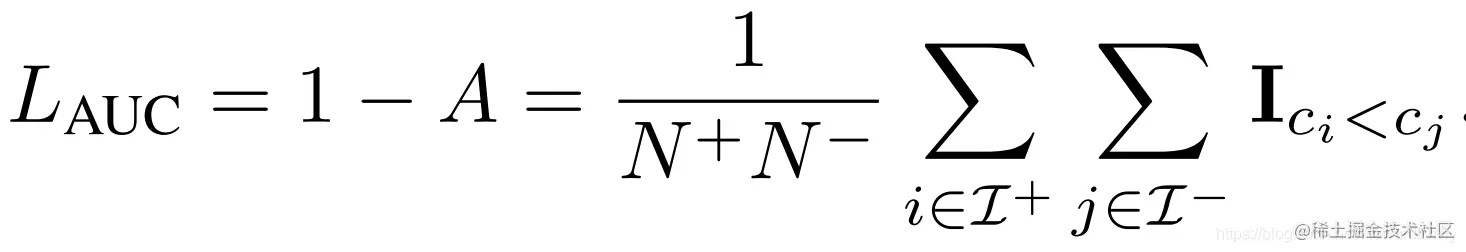 可以看出,AUC就是正负样本错排的损失,即正样本排名低于负样本。所以LAUC=0就是最完美的排序!LAUC和θ相互独立。
可以看出,AUC就是正负样本错排的损失,即正样本排名低于负样本。所以LAUC=0就是最完美的排序!LAUC和θ相互独立。
Method
AUC Risk Without Pairwise Comparison
令(c1↑,c2↑,…,cN↑)为(c1,c2,…,cN)的升序排序,即c1↑<c2↑<⋯<cN↑,令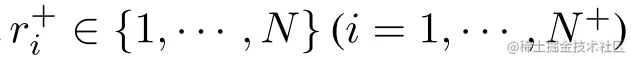 ri为第i个正样本在排序后的列表中的位置; ci↑+为第i个正样本在排序后列表(c1↑,c2↑,…,cN↑)中对应的score,即:ci↑+=cri+↑+.
ri为第i个正样本在排序后的列表中的位置; ci↑+为第i个正样本在排序后列表(c1↑,c2↑,…,cN↑)中对应的score,即:ci↑+=cri+↑+.

上图中假设N+=7,N−=6,(r1+,r2+,r3+,r4+,r5+,r6+,r7+)=(4,6,7,8,9,11,13), 被圆圈圈起来的第二个正样本,它排在两个负样本的前面,因此其对于AUC risk的贡献为: N−+i−ri+.以此类推,对于所有的正负样本错排,我们有:3+2+2+2+2+1+0=12,AUC risk =6×712=72,这与之前介绍的相一致。
根据这一发现,可以得出如下定理:
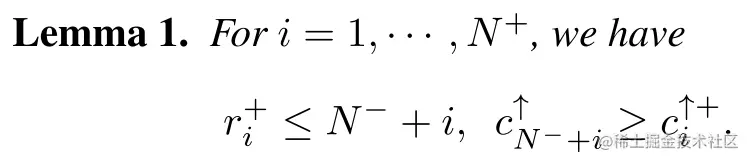 依据该定理,可以很直观的来计算auc正反两对的数量,如上图的例子。
依据该定理,可以很直观的来计算auc正反两对的数量,如上图的例子。
定理2:
当在训练集上的预测没有平局时:
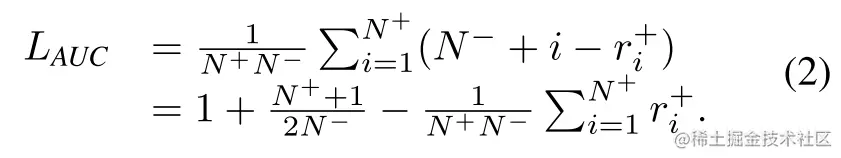
证明:
考虑ri+, 负样本的排名低于第i个正样本的个数为ri+−i,也就是说有N−+i−ri+个负样本排名高于他,(造成一个误排pair)。对所有的错排对进行求和,就得到了上面的结果。
∑i=1N+(N−+i)为预测分数排序列表中的最大的N+个值的下标,∑i=1N+ri+为正样本在排序列表中的下标。因此,公式(2)中定义的AUC风险与两个总和之间的差值成比例。
Univariate Bound on AUC risk
下面开始正式介绍本文的方法....
通过(2)式,可以得到一个新的,基于排序后的预测分数(c1↑,c2↑,…,cN↑)的AUC risk替代损失:
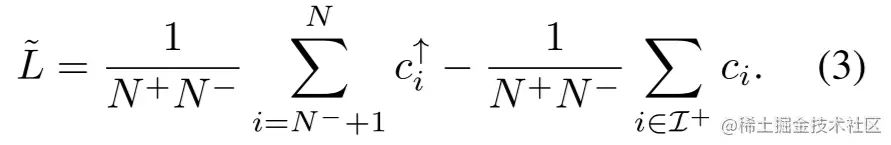
L~非负,因为第二项永远小于等于第一项
Computing L~ without Explicit Ranking
公式(3)需要排序,这仍然是一个很费时的操作。
根据如下定理3,我们可以求出(3)式的一个等价形式,而不需要排序。
定理3:对于N个实数z1<⋯<zN, sum-of-top-k 问题可以等价为:
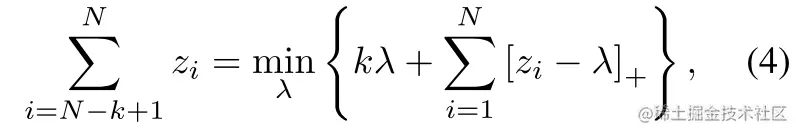 其中最优参数λ∗满足zN−k≤λ∗≤zN−k+1
其中最优参数λ∗满足zN−k≤λ∗≤zN−k+1
证明:
首先我们需要知道,∑N−k+1Nzi为如下线性规划问题的解:
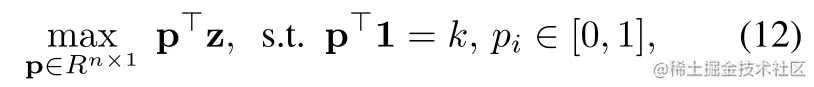 其对应的拉格朗日方程为:
其对应的拉格朗日方程为:
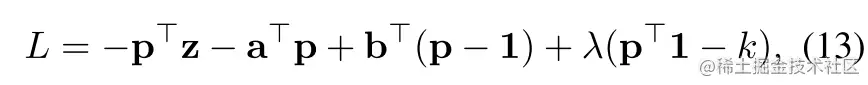 其中a≥0,b≥0,λ为拉格朗日乘子.
将关于L的偏导数p设为0,可以有:
其中a≥0,b≥0,λ为拉格朗日乘子.
将关于L的偏导数p设为0,可以有: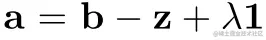 ,
带入(13)式,可以得到(12)式的对偶:
,
带入(13)式,可以得到(12)式的对偶:
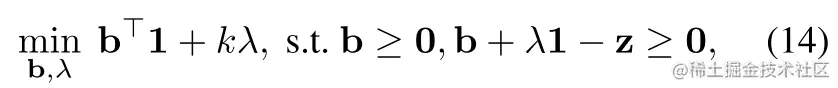 (14)式的限制,告诉我们有:
(14)式的限制,告诉我们有:
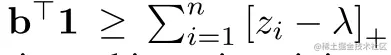 ,当等号成立时,目标函数获得最小值。将其重排可得到(4)式。
更进一步,当我们选择λ∗满足zN−k≤λ∗≤zN−k+1,我们有:
,当等号成立时,目标函数获得最小值。将其重排可得到(4)式。
更进一步,当我们选择λ∗满足zN−k≤λ∗≤zN−k+1,我们有:
kλ∗+i=1∑N[zi−λ∗]+=kλ∗+i=N−k+1∑N(zi−λ∗)=i=N−k+1∑Nzi
根据定理(3),可以将(3)式写成如下形式:
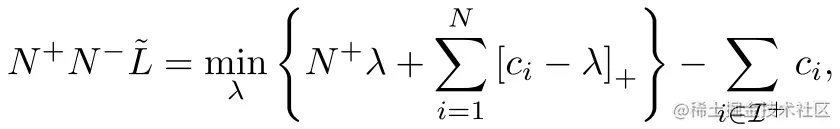
进一步转化为:
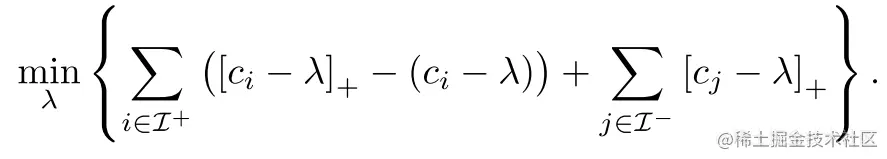
根据hinge loss的属性[a]+−a=[−a]+:
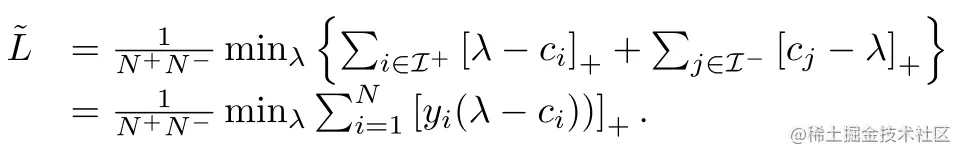 于是,基于L~的数化模型回归,形成的目标函数为:
于是,基于L~的数化模型回归,形成的目标函数为:
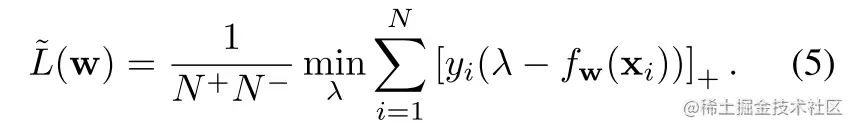 在(5)式中,辅助变量λ可以理解成一个分开两类的阈值,并且与AUC风险的原始定义一样,L~(w)通过在阈值的所有可能值上取总体最小值而独立于阈值的选择。
在(5)式中,辅助变量λ可以理解成一个分开两类的阈值,并且与AUC风险的原始定义一样,L~(w)通过在阈值的所有可能值上取总体最小值而独立于阈值的选择。
L~(w)在二进制分类的上下文中提供了直观的解释,它只惩罚那些预测值低于阈值的正面例子,即[λ−fw(xi)]+,以及负样本预测大于阈值[fw(xi)−λ]+.
此外,根据引理3可知,最优的λ∗∈[cN+↑,cN++1↑)
Relation with SVM Objective
细心的同学们可能发现,当预测函数为线性的情况下fw(x)=wTx, L~(w)和SVM的目标函数有很强的相似性。
重构SVM损失函数:
SVM里分类器一般为w⊤x+b,这里为了方便比较将bias term设置为负的。如果将阈值λ看成是SVM里bias,即w⊤x−λ, SVM的目标函数:
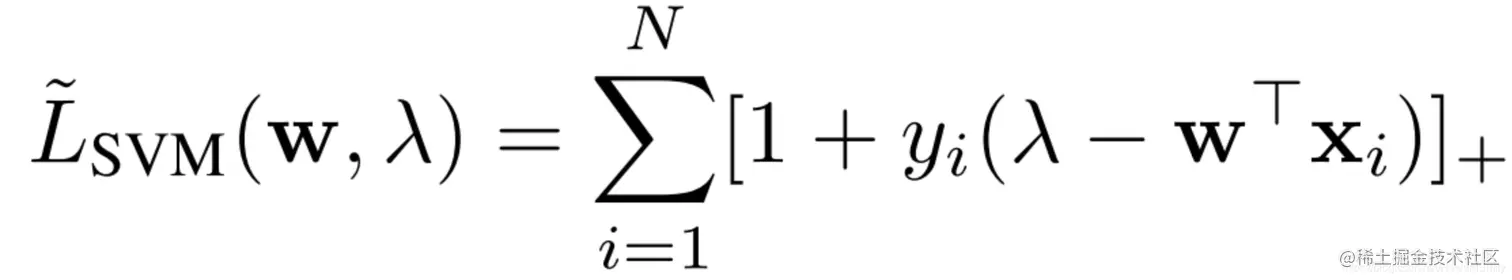 可以看出上式和(5)式一样,都有hinge-loss!
L~SVM(w,λ)是L~(w)的一个upper-bound(上界),因为
可以看出上式和(5)式一样,都有hinge-loss!
L~SVM(w,λ)是L~(w)的一个upper-bound(上界),因为
[1+yi(λ−w⊤xi)]≥[yi(λ−w⊤xi)]
所以,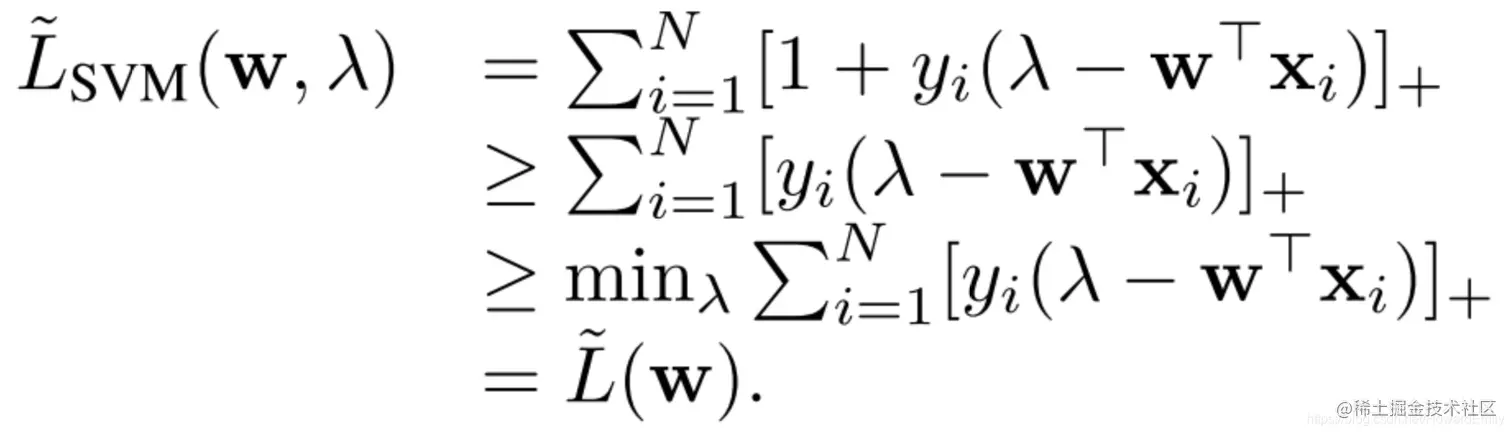 这有助于解释一些长期的实验观察:通过AUC评估,标准SVM的表现不能一直优于其他直接使AUC最大化的方法(因为直接最大化AUC的loss其bound更紧!)
这有助于解释一些长期的实验观察:通过AUC评估,标准SVM的表现不能一直优于其他直接使AUC最大化的方法(因为直接最大化AUC的loss其bound更紧!)
这两个目标函数在两个重要方面也有所不同:
- SVM损失当中的常数1,为分类器需要建立的margin
- L~(w)中的λ在最小化时就没了,而SVM中的λ仍然在.(因为L~(w)的最后λ∗∈[cN+↑,cN++1↑),可以直接迭代优化)
OPTIMIZATION
Resolving Ties in Prediction Scores
直接优化(5)式
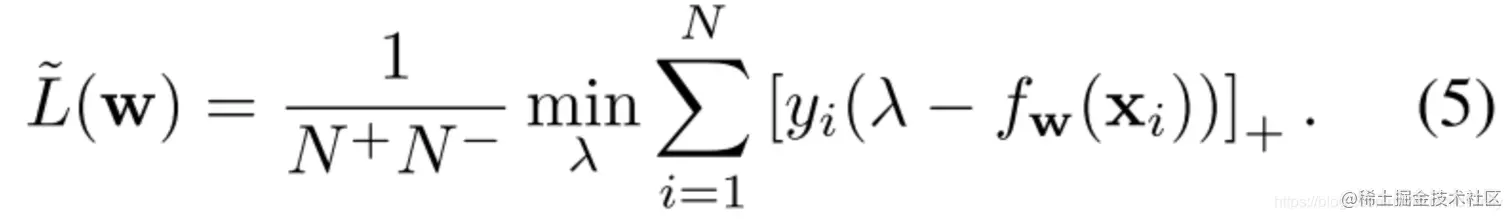 会存在问题: (5)式中w的取值范围不固定,因此,可以通过缩小w的规模来降低学习目标,从而得到w=0的平凡解。
会存在问题: (5)式中w的取值范围不固定,因此,可以通过缩小w的规模来降低学习目标,从而得到w=0的平凡解。
其根本原因是L~(w)的公式是基于预测分数中没有平局的假设,而平凡解对应的是极端相反的结果,即不管数据如何。预测函数总是产生相同的输出(0)。
为了解决这个问题,本文用另外两个项来扩充目标函数:
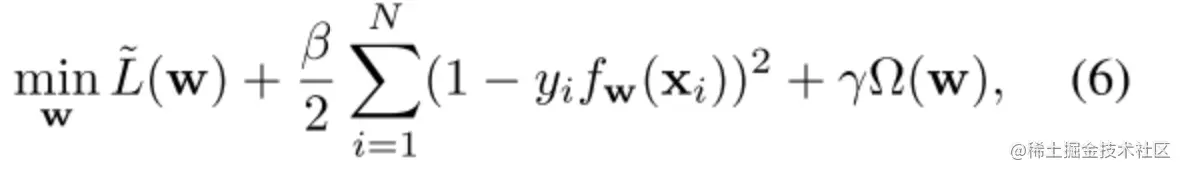
其中第二项对应于一个最小二乘项,以抵消将w集中到零的影响,Ω(w)为正则化项。
Linear Predictor
当fw(x)=w⊤x,Ω(w)=21∣∣w∣∣2时,[x⊤w−λ]+为一个凸函数。
当α∈[0,1],w,w′,λ,λ′:
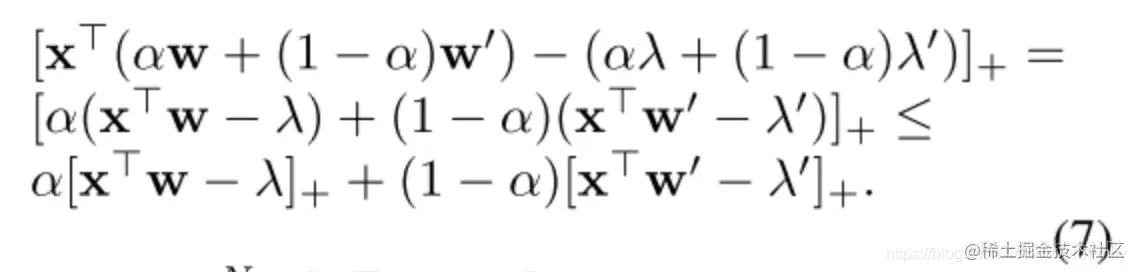 因此∑i=1N[x⊤w−λ]++N+λ为凸函数。min∑i=1N[ci−λ]++N+λ也是凸函数。
因此∑i=1N[x⊤w−λ]++N+λ为凸函数。min∑i=1N[ci−λ]++N+λ也是凸函数。
在线性分类器下,损失函数如下:
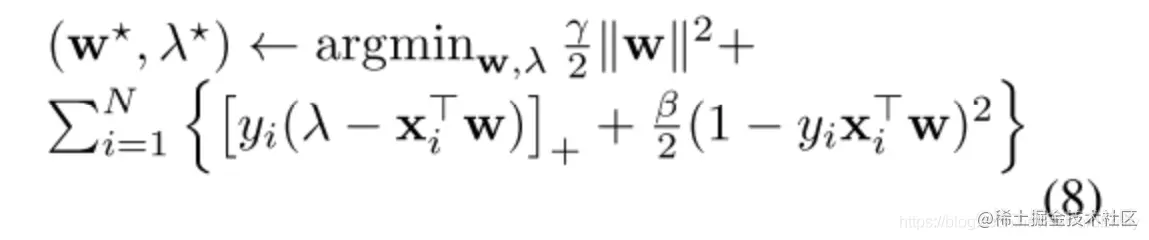
Batch Learning
在batch learning设置下,我们可以知道所有的训练样本,所以可以使用block coordinate descent 算法来优化(8):
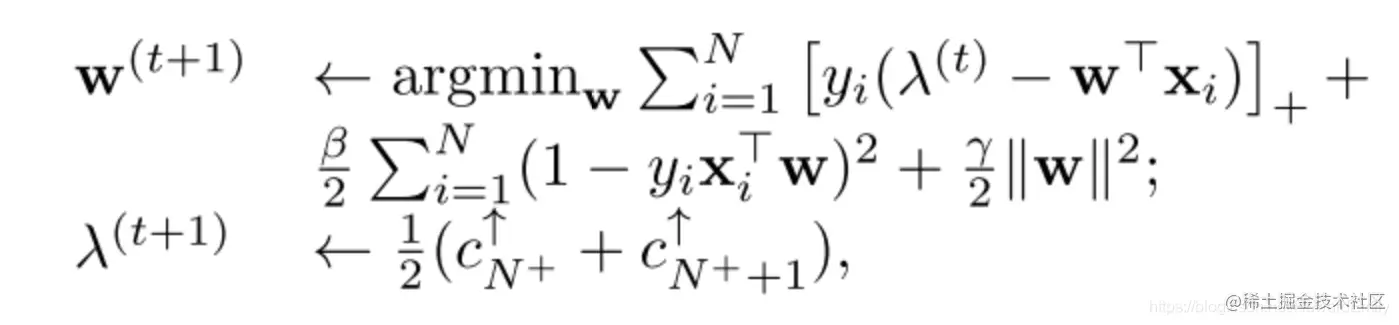 w的优化可以转化为如下受限优化问题:
w的优化可以转化为如下受限优化问题:
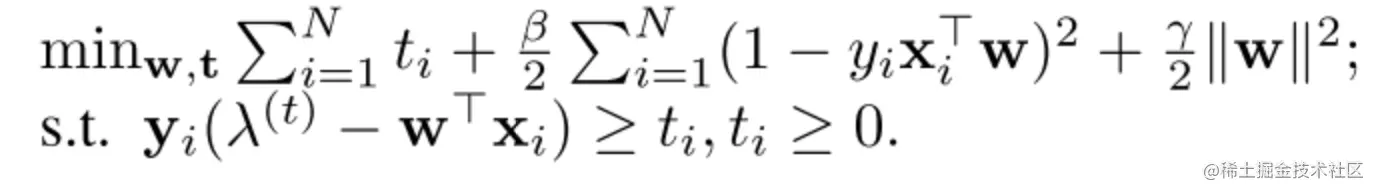
这是一个二次凸优化问题,当w的维数为中低维时,可以用内点法求解。对于高维w,在线学习算法由于避免了建立Hessian矩阵而更加有效。
Online Learning
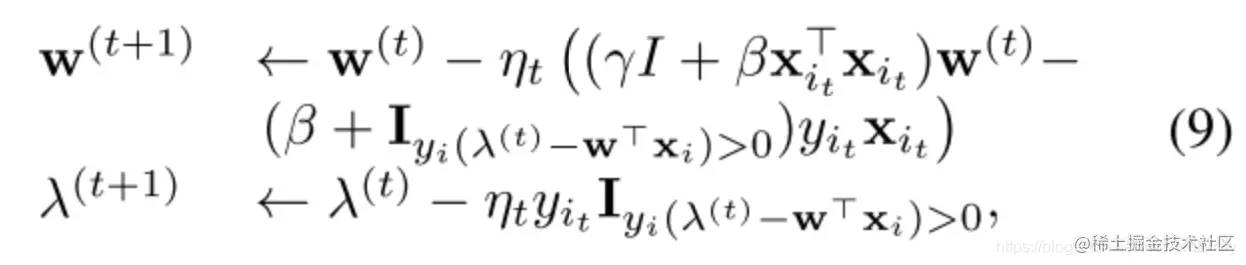 其中步长ηt∼t1.
其中步长ηt∼t1.
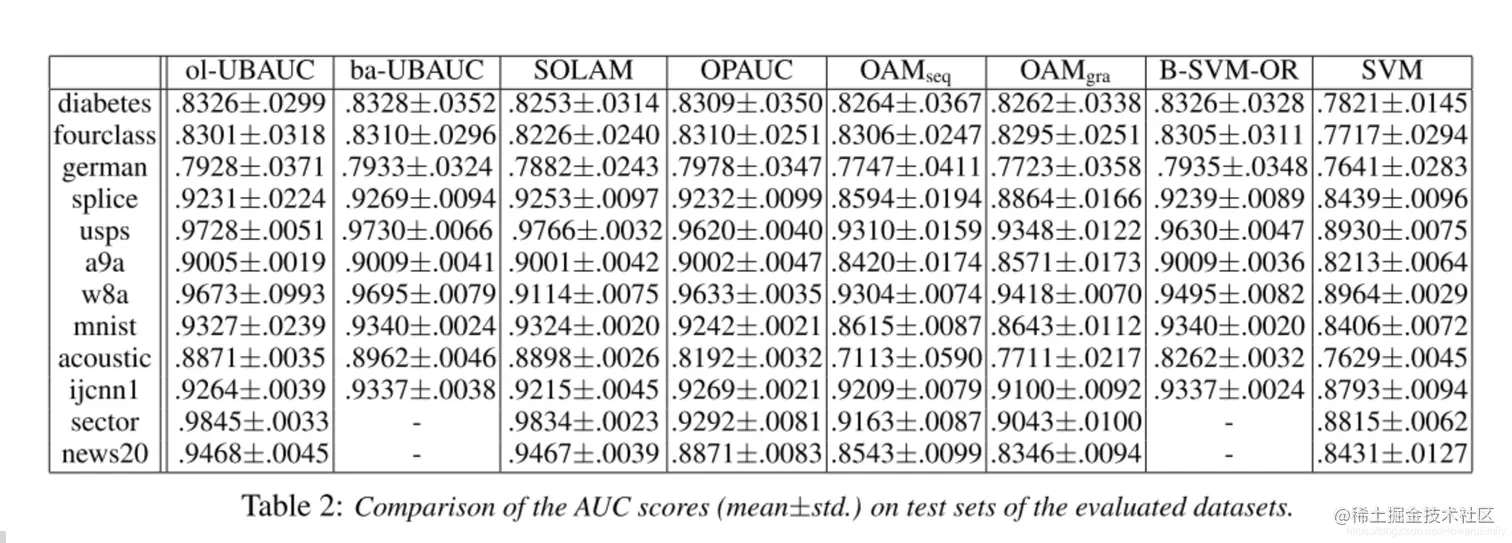
Experiments
同样的,正样本阈值高于的为true positive,计算如下:
AUC risk定义如下:
可以看出,AUC就是正负样本错排的损失,即正样本排名低于负样本。所以就是最完美的排序!和相互独立。
为第i个正样本在排序后的列表中的位置; 为第i个正样本在排序后列表中对应的score,即:.
依据该定理,可以很直观的来计算auc正反两对的数量,如上图的例子。
其中最优参数满足
其对应的拉格朗日方程为:
其中,为拉格朗日乘子. 将关于的偏导数设为,可以有:
, 带入(13)式,可以得到(12)式的对偶:
(14)式的限制,告诉我们有:
,当等号成立时,目标函数获得最小值。将其重排可得到(4)式。 更进一步,当我们选择满足,我们有:
于是,基于的数化模型回归,形成的目标函数为:
在(5)式中,辅助变量可以理解成一个分开两类的阈值,并且与AUC风险的原始定义一样,通过在阈值的所有可能值上取总体最小值而独立于阈值的选择。
可以看出上式和(5)式一样,都有hinge-loss!
是的一个upper-bound(上界),因为
这有助于解释一些长期的实验观察:通过AUC评估,标准SVM的表现不能一直优于其他直接使AUC最大化的方法(因为直接最大化AUC的loss其bound更紧!)
会存在问题: (5)式中的取值范围不固定,因此,可以通过缩小w的规模来降低学习目标,从而得到w=0的平凡解。
因此为凸函数。也是凸函数。
w的优化可以转化为如下受限优化问题:
其中步长.