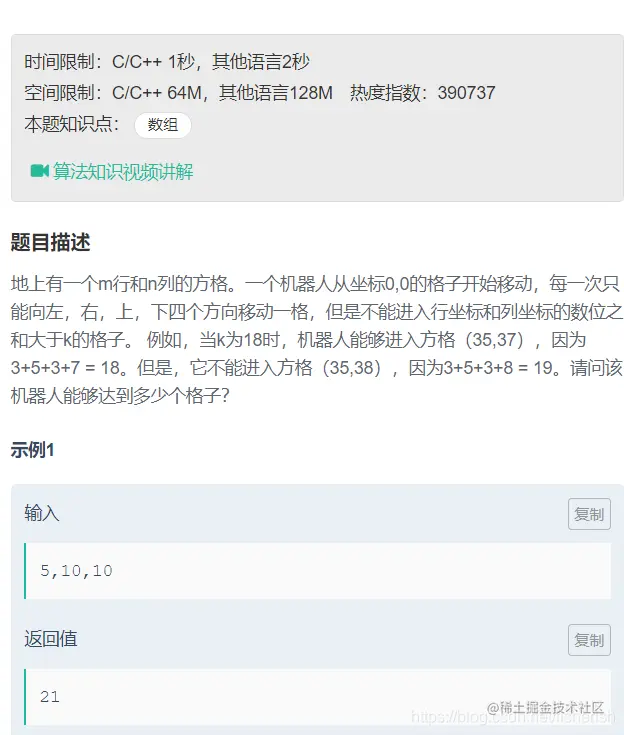
题目描述

题解
// 力扣
// 本题使用的方法为深度优先搜索(DFS),方法和12题的回溯法很像,
// 但其实回溯法是DFS的特殊情况。
// 执行用时:2 ms, 在所有 Java 提交中击败了43.58%的用户
// 内存消耗:35.4 MB, 在所有 Java 提交中击败了84.10% 的用户
class Solution {
private int rows
private int cols
private int k
private int[][] digitSum
private static final int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}}
private int count = 0
// 解题函数
public int movingCount(int m, int n, int k) {
this.rows = m
this.cols = n
this.k = k
if (rows == 0 || cols == 0) // 行或者列其中一个为0,则返回0
return 0
if (k == 0) // 如果k为0,则能到达位置只有(0,0)这第一个位置
return 1
boolean[][] marked = new boolean[rows][cols]
dfs(marked, 0, 0)
return count
}
// 定义搜索函数
// 输入标记矩阵marked,行索引r(初始化为0),列索引c(初始化为0)
private void dfs(boolean[][] marked, int r, int c) {
if (r < 0 || r >= rows || c < 0 || c >= cols) // 超过正常矩阵边界,返回
return
if (marked[r][c]) // 该位置已被遍历过,返回
return
if ((digitSum(r) + digitSum(c)) > k) // 超过数位和的上限,返回
return
count++
marked[r][c] = true
// System.out.println(markedToString(marked))
for (int[] n : next)
dfs(marked, r + n[0], c + n[1])
}
// 定义函数:位数之和
public int digitSum(int n) {
int n0 = n / 1000000000
int n1 = n % 1000000000 / 100000000
int n2 = n % 100000000 / 10000000
int n3 = n % 10000000 / 1000000
int n4 = n % 1000000 / 1000000
int n5 = n % 100000 / 10000
int n6 = n % 10000 / 1000
int n7 = n % 1000 / 100
int n8 = n % 100 / 10
int n9 = n % 10
int sum = n0 + n1 + n2 + n3 + n4 + n5 + n6 +n7 + n8 + n9
return sum
}
// 打印marked的toString函数(不是必须)
public String markedToString(boolean[][] marked) {
StringBuilder res = new StringBuilder()
for (int i = 0
res.append("[");
for (int j = 0; j < marked[0].length
if (marked[i][j])
res.append(" true ")
else
res.append(" false ")
}
res.append("]")
res.append("\r\n")
}
return res.toString()
}
}
// 牛客
// 思路和力扣是一样的
// 运行时间:11ms
// 占用内存:9692k
public class Solution {
private int rows
private int cols
private int threshold
private int[][] digitSum
private static final int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}}
private int count = 0
public int movingCount(int threshold, int rows, int cols) {
this.rows = rows
this.cols = cols
this.threshold = threshold
if (rows == 0 || cols == 0)
return 0
if (threshold == 0)
return 1
boolean[][] marked = new boolean[rows][cols]
dfs(marked, 0, 0)
return count
}
private void dfs(boolean[][] marked, int r, int c) {
if (r < 0 || r >= rows || c < 0 || c >= cols)
return
if (marked[r][c])
return
if ((digitSum(r) + digitSum(c)) > threshold)
return
count++
marked[r][c] = true
// System.out.println(markedToString(marked))
for (int[] n : next)
dfs(marked, r + n[0], c + n[1])
}
// 定义函数:位数之和
public int digitSum(int n) {
int n0 = n / 1000000000
int n1 = n % 1000000000 / 100000000
int n2 = n % 100000000 / 10000000
int n3 = n % 10000000 / 1000000
int n4 = n % 1000000 / 1000000
int n5 = n % 100000 / 10000
int n6 = n % 10000 / 1000
int n7 = n % 1000 / 100
int n8 = n % 100 / 10
int n9 = n % 10
int sum = n0 + n1 + n2 + n3 + n4 + n5 + n6 +n7 + n8 + n9
return sum
}
// 打印marked的toString函数(不是必须)
public String markedToString(boolean[][] marked) {
StringBuilder res = new StringBuilder()
for (int i = 0
res.append("[");
for (int j = 0; j < marked[0].length
if (marked[i][j])
res.append(" true ")
else
res.append(" false ")
}
res.append("]")
res.append("\r\n")
}
return res.toString()
}
}