浑元功法：排序

冒泡排序

基本原理

1. 比较相邻的元素，如果第一个比第二个大，就交换
2. 依次比较相邻的元素，直到比较完成
3. 重复步骤1-步骤2的操作

演示

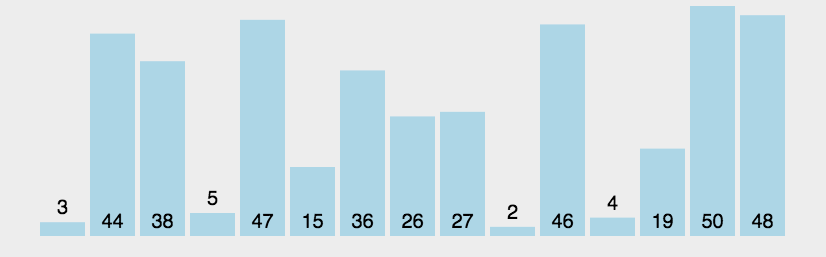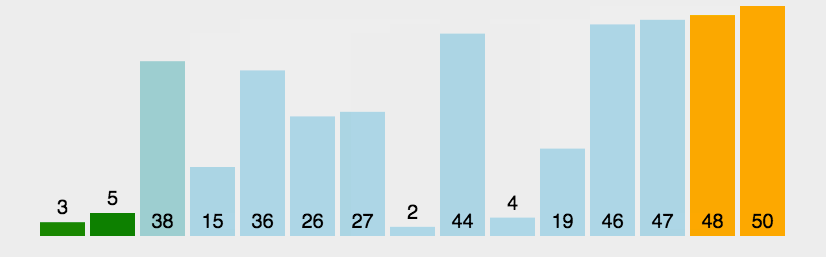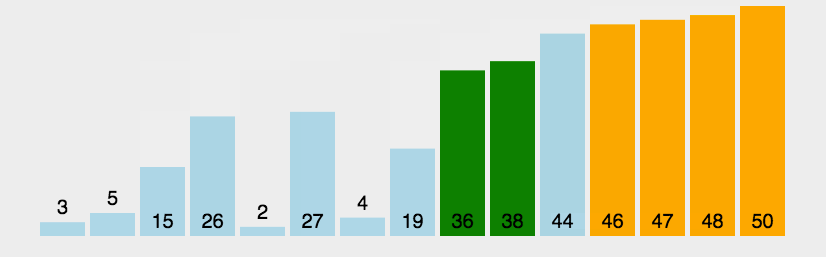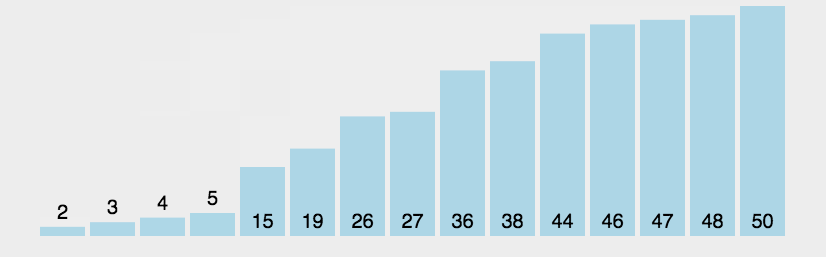
复杂度

平均	最坏	最好	稳定性	空间复杂度
O(n^2)	O(n^2)	O(n)	稳定	O(1)

• 最好情况：正序数组

代码实现

function bubbleSort(arr) {
  if (arr.length < 2) return arr;
  for (var i = 0; i < arr.length; i++) {
    for (var j = 0; j < arr.length-1-i; j++) {
      if (arr[j] > arr[j+1]) {
        var temp = arr[j];
        arr[j] = arr[j+1];
        arr[j+1] = temp;
      }
    }
  }
  return arr;
}

选择排序

基本原理

1. 遍历数组，把最小的元素找出来，放在首部
2. 把剩下的元素看成一个新的数组
3. 重复步骤1-步骤2的操作，直到完成排序

演示

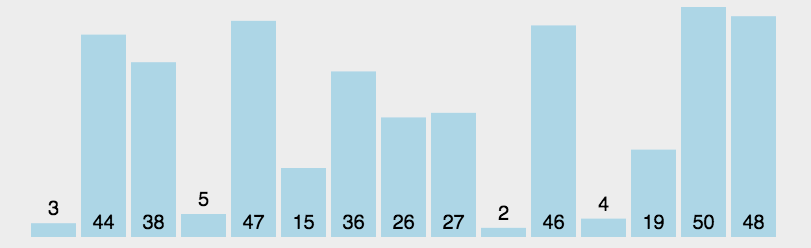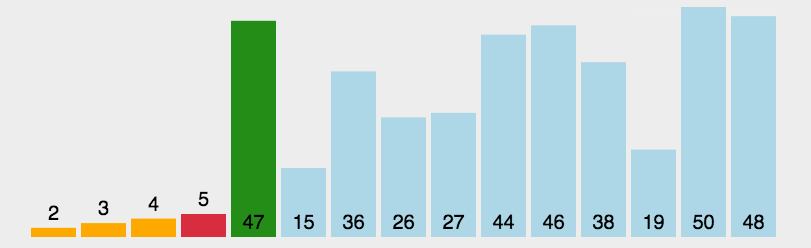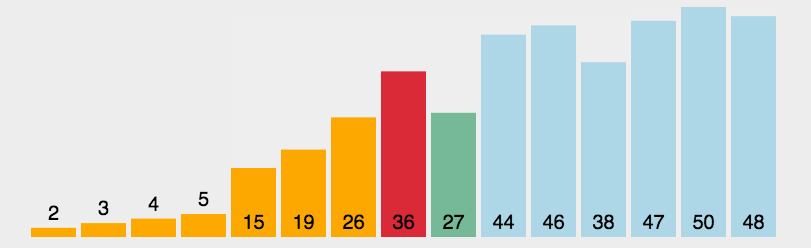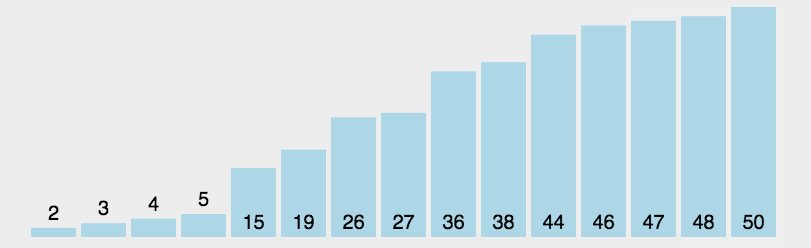
复杂度

平均	最坏	最好	稳定性	空间复杂度
O(n^2)	O(n^2)	O(n^2)	不稳定	O(1)

• 最好情况，数组已经排序好了，但是还是需要比较n(n-1)/2次

代码实现

function selectionSort(arr) {
  if (arr.length < 2) return arr;
  var temp = 0;
  for (var i = 0; i < arr.length-1; i++) {
    var minIndex = i;
    for (var j = i+1; j < arr.length; j++) {
      if (arr[minIndex] > arr[j]) {
        minIndex = j;
      }
    }
    if (minIndex != i) {
      temp = arr[minIndex];
      arr[minIndex] = arr[i];
      arr[i] = temp;
    }
  }
}

快速排序

基本原理

1. 对于一个未排序的数组，取一个元素作为基准值pivotKey
2. 将小于该基准值的元素放在左边，大于该基准值的元素放在右边
3. 以该基准值为中间，将数组分为左右两部分
4. 对左右两部分分别进行步骤1-步骤3的操作，直到完成排序

演示

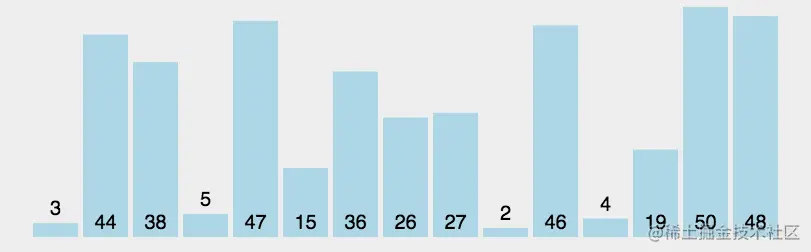
复杂度

平均	最坏	最好	稳定性	空间复杂度
O(nlog(n))	O(n^2)	O(nlog(n))	不稳定	O(log(n))

• 最坏情况：正序排列的数组
• 最好情况：每一次分割都能平分

代码实现

function quickSort(arr) {
  if (arr.length < 2) return arr;
  var pivotKey = arr[0];
  var pivotArr = [];
  var lowArr = [];
  var highArr = [];
  arr.forEach(current => {
    if (current == pivotKey) {
      pivotArr.push(current);
    } else if (current > pivotKey) {
      highArr.push(current);
    } else {
      lowArr.push(current);
    }
  });
  return quickSort(lowArr).concat(pivotArr).concat(quickSort(highArr));
}

归并排序

基本原理

1. 将数组分为两个数组
2. 对分割好的数组进行步骤1的操作
3. 将拆分好的数组进行排序，形成新的数组
4. 将新的数组合并

演示

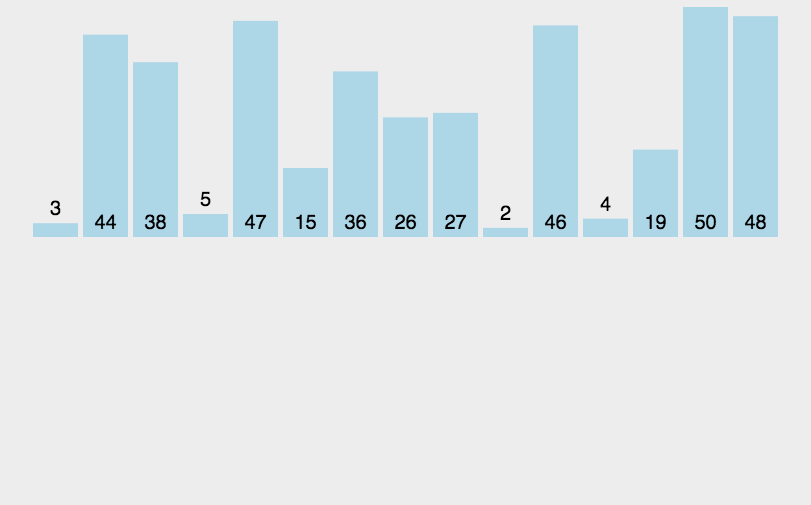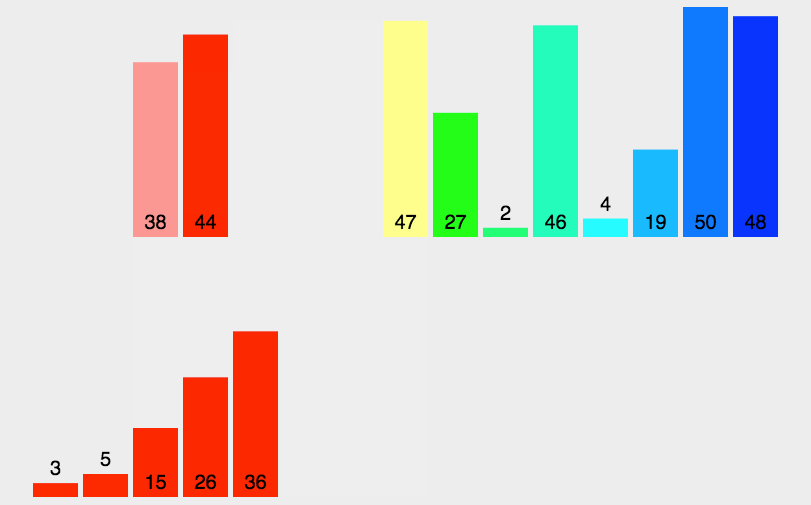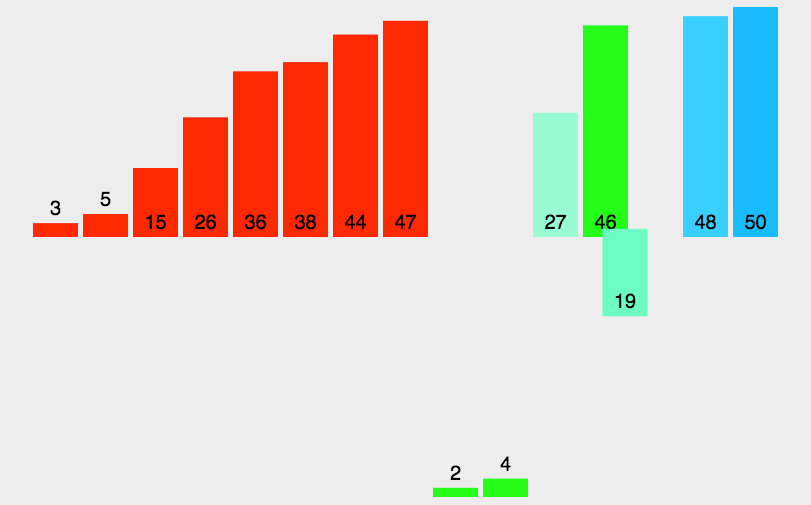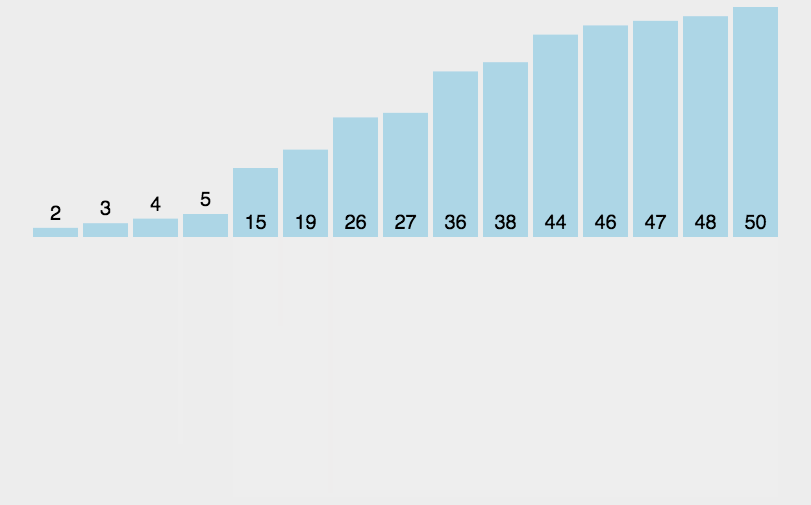
复杂度

平均	最坏	最好	稳定性	空间复杂度
O(nlog(n))	O(nlog(n))	O(nlog(n))	稳定	O(n+log(n))

代码实现

function mergeSort(arr) {
  if (arr.length == 1) return arr;
  const length = arr.length;
  const middle = Math.floor(length/2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);
  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;
  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }
  return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex));
}

插入排序

基本原理

1. 从第一个元素开始
2. 取下一个元素，在已经排序的元素队列中从后往前扫描
3. 如果该元素大于新元素，则交换位置
4. 重复步骤3的操作，直到找到已排序的元素小于或等于新元素
5. 重复步骤2-步骤4的操作

演示

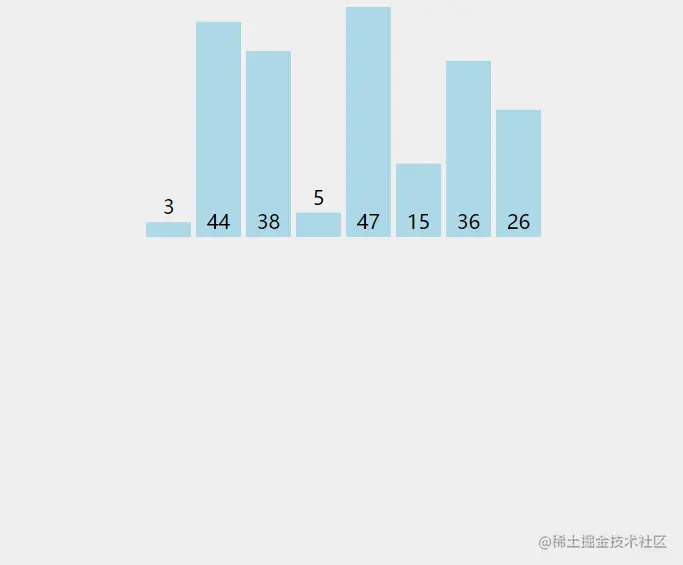
复杂度

平均	最坏	最好	稳定性	空间复杂度
O(n^2)	O(n^2)	O(n)	稳定	O(1)

• 最好情况：正序排列的数组

代码实现

function insertSort(arr) {
  if (arr.length < 2) return arr;
  for (var i = 1; i < arr.length; i++) {
    for (var j = i; j > 0; j--) {
      if (arr[j] < arr[j-1]) {
        var temp = arr[j];
        arr[j] = arr[j-1];
        arr[j-1] = temp;
      }
    }
  }
  return arr;
}