参考

参考博文：blog.csdn.net/b954960630/…
学习Node.js的B站视频：www.bilibili.com/video/BV1Ns…

TSP问题

旅行商问题是一个np难问题，此文是笔者最近学了Node.js和刚好需要做一份遗传算法解决TSP问题，就写了这一篇博文。
TSP问题是组合数学中一个古老而又困难的问题，也是一个典型的组合优化问题，现已归入NP完备问题类。NP问题用穷举法不能在有效时间内求解，所以只能使用启发式搜索。而遗传算法是求解此类问题比较实用、有效的方法之一。

问题描述

假设有n个可直达的城市，一销售商从其中的某一城市出发，不重复地走完其余n-1个城市并回到原出发点，在所有可能的路径中求出路径长度最短的一条（任意两个城市可以相互直达）。
给出30个城市的位置信息表 | 城市编号 | 坐标 |城市编号|坐标|城市编号|坐标| |----------|-------|------|----|------|----| |1 |(87，7) | 11| (58，69)| 21| (4，50)| |2 |(91，38)| 12| (54，62)| 22| (13，40)| |3 |(83，46)| 13| (51，67)| 23| (18，40)| |4 |(71，44)| 14| (37，84)| 24| (24，42)| |5 |(64，60)| 15| (41，94)| 25| (25，38)| |6 |(68，58)| 16| (2，99) | 26| (41，26)| |7 |(83，69)| 17| (7，64) | 27| (45，21)| |8 |(87，76)| 18| (22，60)| 28| (44，35)| |9 |(74，78)| 19| (25，62)| 29| (58，35)| |10 |(71，71)| 20|(18，54) | 30| (62，32)|
距离：两城市的直线距离
- 如：计算城市c1和c2的距离 - dx = |x1 - x2|, dy = |y1 - y2|, d = Math.sqrt(dxdx + dydy)

算法流程

轮盘赌法选择后代 |种群中的个体 |1|2|3|4|5|6| |------------|-|-|-|--|--|---| |适应值 |8 |2|17|7|4|11| |轮盘赌法范围 |0~~7 |8~~9 |10~~26 | 27~~33 |34~~37 | 38~~48 | |产生的随机数| 23属于10~26的范围 |选中的后代 | 因此选中3个体
染色体交叉
- 现在Parent1选取连续的一段基因A（数组元素），然后再从Parent2中选取不重复于A中基因组合B，然后将A、B拼接起来
- Parent1 -> 3 7 8 6 1 9 2 4 5
  - A -> 8 6 1 9
- Parent2 -> 8 2 6 9 4 5 3 1 7
  - B -> 2 4 5 3 7
- child -> 8 6 1 9 2 4 5 3 7
  - A + B -> 8 6 1 9 2 4 5 3 7
变异（针对种群中除去最优的个体，使其有几率发生往好的方向变异）
- 为了脱离染色体交叉可能陷入的局部最优
- 选取两个基因的下标，记为gen1，gen2，m = Math.floor（gen1 + gen2）/ 2
  - 将a[gen1...m]与a[m+1...gen2]依次交换位置

 // 交换基因的位置gen1 、 gen2    -    1 ~ (CITY_NUM - 1)
        let gen1 = Math.floor(Math.random() * (CITY_NUM - 1)) + 1
        let gen2 = Math.floor(Math.random() * (CITY_NUM - 1)) + 1
        // 保证gen2 >= gen1
        if(gen1 > gen2) {
          let temp = gen1
          gen1 = gen2
          gen2 = temp
        }
        // 交换gen1 和 gen2
        // let tt = t_colony[gen2]
        // t_colony[gen2] = t_colony[gen1]
        // t_colony[gen1] = tt
        for(let m = gen1; m < Math.floor((gen1 + gen2) / 2); m ++) {
          let temp = t_colony[m]
          t_colony[m] = t_colony[gen1 + gen2 - m]
          t_colony[gen1 + gen2 - m] = temp
        }

计算适应值
- 采用N-obj：N是一个极大数，obj是个体的总路径之和，适应值越大，说明此个体越适应
具体算法代码细节，可以看原代码，我每行注释的很清晰
- 但要注意的是求解30个城市和10个城市的问题切换需要修改的地方
- Tsp.js
- module/init/const.js
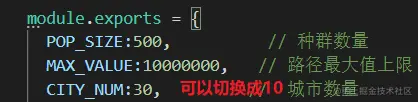
- module/Cross.js

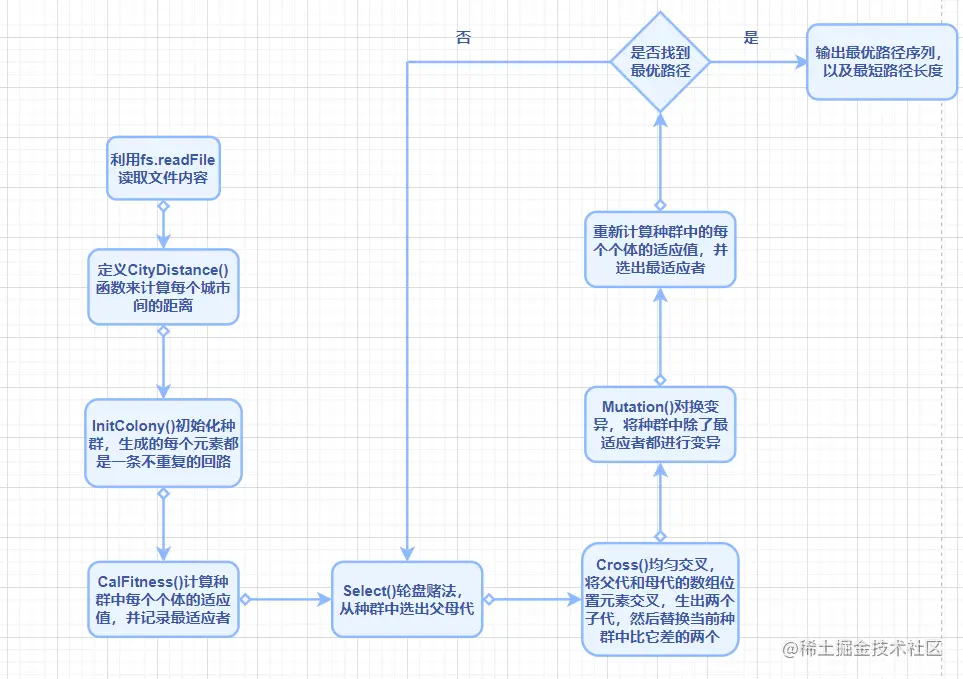
算法目录解析

Tsp.js：算法的入口文件，负责导入各种功能模块
module文件夹
- data.json：存储30个城市的数据
- data1.json：存储前10个城市的数据
- Select.js：从种群中通过轮盘赌法选择父代和母代
- Mutation.js：子代的染色体发生变异
- Copy：将一个数组的元素赋值到另一个数组中
- Cross.js：父母染色体按某种方式进行交叉（数组元素按位置进行交换）
- GetFittness.js：获取某个个体的适应值
- init文件夹中的文件负责种群的初始化工作
  - const.js（存储相关的系统常量）
  - CityDistance.js：计算每个城市间的距离
  - InitColony.js：初始化种群
  - Check.js：检查新生成的个体是否已经存在当前种群中
  - CalFitness：计算种群中每个个体的适应值

最优解和实验结果分析

30个城市

最优解：1 2 3 4 6 5 7 8 9 10 11 12 13 14 15 16 17 19 18 20 21 22 23 24 25 28 26 27 29 30
实验结果分析
- 其路径长度为：424.869292

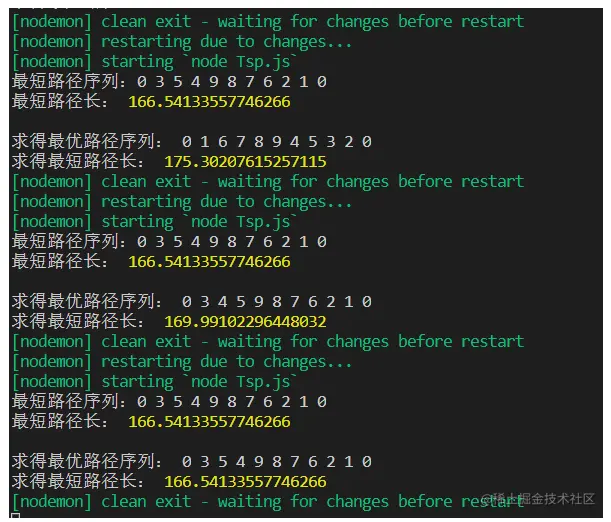
10个城市

最优解： 0 3 5 4 9 8 7 6 2 1 0
实验结果分析
- 路径长度是166.541336

源代码

data.json

[
  {
    "x":87,
    "y":7
  },
  {
    "x":91,
    "y":38
  },
  {
    "x":83,
    "y":46
  },
  {
    "x":71,
    "y":44
  },
  {
    "x":64,
    "y":60
  },
  {
    "x":68,
    "y":58
  },
  {
    "x":83,
    "y":69
  },
  {
    "x":87,
    "y":76
  },
  {
    "x":74,
    "y":78
  },
  {
    "x":71,
    "y":71
  },
  {
    "x":58,
    "y":69
  },
  {
    "x":54,
    "y":62
  },
  {
    "x":51,
    "y":67
  },
  {
    "x":37,
    "y":84
  },
  {
    "x":41,
    "y":94
  },
  {
    "x":2,
    "y":99
  },
  {
    "x":7,
    "y":64
  },
  {
    "x":22,
    "y":60
  },
  {
    "x":25,
    "y":62
  },
  {
    "x":18,
    "y":54
  },
  {
    "x":4,
    "y":50
  },
  {
    "x":13,
    "y":40
  },
  {
    "x":18,
    "y":40
  },
  {
    "x":24,
    "y":42
  },
  {
    "x":25,
    "y":38
  },
  {
    "x":41,
    "y":26
  },
  {
    "x":45,
    "y":21
  },
  {
    "x":44,
    "y":35
  },
  {
    "x":58,
    "y":35
  },
  {
    "x":62,
    "y":32
  }
]

data1.json

[
  {
    "x":87,
    "y":7
  },
  {
    "x":91,
    "y":38
  },
  {
    "x":83,
    "y":46
  },
  {
    "x":71,
    "y":44
  },
  {
    "x":64,
    "y":60
  },
  {
    "x":68,
    "y":58
  },
  {
    "x":83,
    "y":69
  },
  {
    "x":87,
    "y":76
  },
  {
    "x":74,
    "y":78
  },
  {
    "x":71,
    "y":71
  }
]

Tsp.js

// 导入常量
const MAX_EPOC = require('./module/init/const.js').MAX_EPOC
let COUNT = require('./module/init/const.js').COUNT

// 计算城市间的距离
const CityDistance = require('./module/init/CityDistance.js')
// 初始化种群
const InitColony = require('./module/init/InitColony.js')
// 初始计算适应值
const CalFitness = require('./module/init/CalFitness.js')
// 轮盘赌法 选择算子
const Select = require('./module/Select.js')
// 染色体交叉
const Cross = require('./module/Cross.js')
// 对换变异
const Mutation = require('./module/Mutation.js')

class TSP {
  colony = []  // 城市种群,二维数组
  fitness = [] // 每个个体适应值，下标代表哪个 个体
  Distance = [] // 每个个体的总路径，下标代表哪个 个体

  BestRooting = [] // 最优城市路径序列
  BestFitness = [] // 最优路径适应值，
  BestPath= null // 最优路径长度
  BestIndex = null // 最适应者的下标

  SelectParent = [] // 记录选择的个体的下标
}
let city = new TSP()

const fs = require('fs')

fs.readFile('./data1.json',(err,data) => {
  if(err) {
    return err
  }
  const tsp_data = JSON.parse(data.toString()) // 各城市坐标
  let distance = CityDistance(tsp_data) // 返回二维数组,记录个城市的距离
  InitColony(city,tsp_data) // 初始化数量为300的种群，每个是一条不重复的回路
  CalFitness(city,distance) // 计算种群每个个体的适应值，并选出最适应者

  // for(let i = 0; i < MAX_EPOC; i ++) { 
    
    // console.log('循环次数:',COUNT ++,"路径序列：",city.BestRooting.join(' '),"路径长：",city.BestPath)
  while(city.BestRooting.join(' ') != '0 3 5 4 9 8 7 6 2 1 0'){
  // while(city.BestRooting.join(' ') != '0 1 2 3 5 4 6 7 8 9 10 11 12 13 14 15 16 18 17 19 20 21 22 23 24 27 25 26 28 29 0'){
    // console.log(city.Distance.length)
    // console.log(city.colony)
    // console.log('循环次数：',COUNT ++,"路径长：",city.BestPath,"路径序列：",city.BestRooting.join(' '))
    // 选择（轮盘赌法）
    Select(city)
    // 均匀交换
    Cross(city,distance)
    // 对换变异
    Mutation(city,distance)
    // 计算适应值（N / 个体的路径和）
    CalFitness(city,distance)
    // console.log(city.colony)
    console.log('循环次数：',COUNT ++,"路径长：",city.BestPath,"路径序列：",city.BestRooting.join(' '))
  }
  // console.log(city.fitness)
  console.log("\n求得最优路径序列：",city.BestRooting.join(' '))
  console.log("求得最短路径长：",city.BestPath)
  // console.log("求得最优适应值：",city.BestFitness)
})

module文件夹

Select.js

const POP_SIZE = require('./init/const').POP_SIZE

module.exports = function(city) {
  city.SelectParent = []
  /*
    0 ~ SelectP[1]
    SelectP[1] ~ SelectP[2]
    ...
    SelectP[POP_SIZE - 2] ~ SelectP[POP_SIZE - 1] 
  */
  let SelectP = [0]
  // 1、建立好 轮盘区间
  for(let i = 0; i < POP_SIZE; i ++) {
    SelectP[i + 1] = SelectP[i] + city.fitness[i]
  }

  // 2、随机选择 - [ 0 ~ SelectP[POP_SIZE - 1] )
  let r1 = Math.random() * SelectP[POP_SIZE - 1]
  let r2 = Math.random() * SelectP[POP_SIZE - 1]
  // 判断 r1、r2分别处于哪个区间
  for(let i = 0; i < POP_SIZE - 1; i ++) {
    if(r1 >= SelectP[i] && r1 <= SelectP[i + 1]) {
      // 属于 i
      city.SelectParent.push(i)
      break
    }
  }
  for(let j = 0; j < POP_SIZE - 1; j ++) {
    if(r2 >= SelectP[j] && r2 <= SelectP[j + 1]) {
      // 属于 i
      city.SelectParent.push(j)
      break
    }
  }
  // console.log(city.SelectParent)
}

Mutation.js

let {POP_SIZE,CITY_NUM} = require('./init/const')

const Copy = require('./Copy.js')
const GetFittness = require('./GetFittness.js')

// 除了最适应者，都将其进行对换变异
module.exports = function(city,distance) {
  // 做 k 次交换
  for(let i = 0; i < POP_SIZE; i ++) {
    // 临时记录低 i 个个体
    // let i
    let t_colony = []
    let flag = 0
    let count = 0
    do{
      // 随机产生 0 ~ POP_SIZE
      // i = Math.floor(Math.random() * POP_SIZE)
      // console.log(i)
      // 保证最优个体不变异
      if(i != city.BestIndex) {
        Copy(t_colony,city.colony[i])

        // console.log(t_colony)
        
        // 交换基因的位置gen1 、 gen2    -    1 ~ (CITY_NUM - 1)
        let gen1 = Math.floor(Math.random() * (CITY_NUM - 1)) + 1
        let gen2 = Math.floor(Math.random() * (CITY_NUM - 1)) + 1
        // 保证gen2 >= gen1
        if(gen1 > gen2) {
          let temp = gen1
          gen1 = gen2
          gen2 = temp
        }
        // 交换gen1 和 gen2
        // let tt = t_colony[gen2]
        // t_colony[gen2] = t_colony[gen1]
        // t_colony[gen1] = tt
        for(let m = gen1; m < Math.floor((gen1 + gen2) / 2); m ++) {
          let temp = t_colony[m]
          t_colony[m] = t_colony[gen1 + gen2 - m]
          t_colony[gen1 + gen2 - m] = temp
        }

        // console.log(t_colony)
        if(GetFittness(t_colony,distance) > GetFittness(city.colony[i],distance)) {
          // if(i == city.BestIndex) {
          //   console.log("变异后Fittness：",GetFittness(t_colony,distance),"变异前Fittness：",GetFittness(city.colony[i],distance))
          // }
          // console.log(city.colony)
          // 交换 好的变异 后的
          Copy(city.colony[i],t_colony)
          flag = 1
        }
        count ++
      } 
    }while(t_colony.length && flag == 0 && count < 3) // 一定要适应值变大

  }
}

GetFittness.js

const {CITY_NUM,N} = require("./init/const")

module.exports = function(colony,distance) {
  let start,end
  let distance_sum = 0
  // console.log(colony,arguments[2])
  // console.log(distance.length)
  // console.log(CITY_NUM)
  for(let i = 0; i < CITY_NUM; i ++) {
    start = colony[i]
    end = colony[i + 1]
      // console.log(end)
    distance_sum += distance[start][end]
  }
  // console.log(distance_sum)
  return N / distance_sum
}

Cross.js

const POP_SIZE = require('./init/const').POP_SIZE
const CITY_NUM = require('./init/const').CITY_NUM
const N = require('./init/const').N

const fs = require('fs')

module.exports = function(city,distance) {
  /*
    [0...0]长度为30的路径序列
    随机从 父亲中，找到 15 长度的区间
    然后从 母亲中，找到 不重复的 15 个数塞进去
  */
  let father = city.colony[ city.SelectParent[0] ]
  let mother = city.colony[ city.SelectParent[1] ]
  // console.log(father.sort((a,b) => a - b),mother.sort((a,b) => a - b))
  // console.log(father,mother)
  // 1、产生 1 ~ 15 随机数
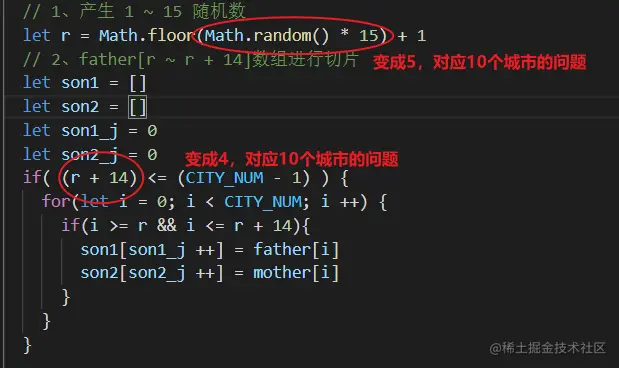
  let r = Math.floor(Math.random() * 5) + 1
  // 2、father[r ~ r + 14]数组进行切片
  let son1 = []
  let son2 = []
  let son1_j = 0
  let son2_j = 0
  if( (r + 4) <= (CITY_NUM - 1) ) {
    for(let i = 0; i < CITY_NUM; i ++) {
      if(i >= r && i <= r + 4){
        son1[son1_j ++] = father[i]
        son2[son2_j ++] = mother[i]
      }
    }
  }

  // console.log(r,son1,son1.length)
  // console.log(r,son2,son2.length)
  mother.forEach((ele,index) => {
    let flag = 1
    for(let i = 0; i < son1.length; i ++) {
      if(ele == son1[i])
        flag = 0
    }
    // console.log(son1,son1.length)
    if(flag == 1 && ele != 0) {
      if(index < r)
        son1.unshift(mother[index])
      else
        son1.push(mother[index])
    }
  })
  father.forEach((ele,index) => {
    let flag = 1
    for(let i = 0; i < son2.length; i ++) {
      if(ele == son2[i])
        flag = 0
    }
    // console.log(son2,son2.length)
    if(flag == 1 && ele != 0) {
      if(index < r)
        son2.unshift(father[index])
      else
        son2.push(father[index])
    }
  })
  // 最后首尾补0
  son1.unshift(0)
  son1.push(0)
  son2.unshift(0)
  son2.push(0)
  // console.log(son1,son2)
  // console.log(r,son1.sort((a,b) => a - b),son1.length)
  // console.log(r,son2.sort((a,b) => a - b),son2.length)

  // 计算 son1、son2的距离总和
  let son1_distance = 0
  let son2_distance = 0
  // console.log(distance.length)
  for(let i = 0; i < CITY_NUM; i ++) {
    son1_distance += distance[ son1[i] ][ son1[i + 1] ]
    son2_distance += distance[ son2[i] ][ son2[i + 1] ]
  }
  // console.log(son1_distance)
  // console.log(son2_distance) 
  // 计算son1、son2的fitness
  let son1_fitness = N / son1_distance
  let son2_fitness = N / son2_distance
  
  // 将原种群中适应度比 子代低的去除掉
  let flag1 = 0
  let flag2 = 0
  for(let k = 0; k < POP_SIZE; k ++) {
    if(flag1 == 0 && city.fitness[k] < son1_fitness) {
      city.fitness[k] = son1_fitness
      city.colony[k] = son1
      city.Distance[k] = son1_distance

      flag1 = 1
    }else if(flag2 == 0 && city.fitness[k] < son2_fitness) {
      city.fitness[k] = son2_fitness
      city.colony[k] = son2
      city.Distance[k] = son2_distance
      
      flag2 = 1
    }
  }
}

Copy

// 一个数组元素复制到另一个数组元素
module.exports = function(arr2,arr1) {
  let i = 0
  for(let ele of arr1) {
    arr2[i++] = ele
  }
}

init文件夹

const.js


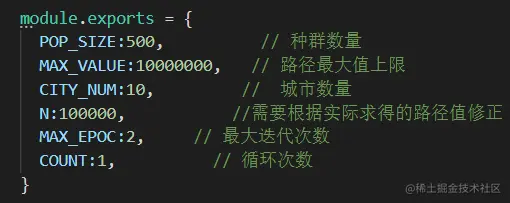
module.exports = {
  POP_SIZE:500,          // 种群数量
  MAX_VALUE:10000000,   // 路径最大值上限
  CITY_NUM:10,         //  城市数量
  N:100000,           //需要根据实际求得的路径值修正
  MAX_EPOC:2,     // 最大迭代次数
  COUNT:1,          // 循环次数
}

initColony.js

const check = require('./Check.js')
const POPSIZE = require('./const').POP_SIZE
const MAXVALUE = require('./const').MAX_VALUE
const CITY_NUM = require('./const').CITY_NUM

module.exports = function(city,tsp_data) {
  for(var i = 0; i < POPSIZE; i ++) {
    if(!city.colony[i])
      city.colony[i] = []
    city.colony[i][0] = 0
    city.colony[i][CITY_NUM] = 0
    city.BestIndex = MAXVALUE
    city.BestFitness = 0 // 适应值越大越好
  }

  for(var i = 0; i < POPSIZE; i ++) {
    for(var j = 1; j < CITY_NUM; j ++) {
      // 随机获取到 1 ~ CITY_NUM - 2
      let r = Math.floor(Math.random() * (CITY_NUM - 1)) + 1  
      // 检查生存的r是否合理，合理才赋值！
      while(check(city,i,j,r))
      {
          r = Math.floor(Math.random() * (CITY_NUM - 1)) + 1  
      }
      city.colony[i][j] = r;
    }
  }
}

cityDistance.js

// 计算城市间的距离
// 用二维数组存储
module.exports = function(tsp_data) {
  let res = []
  // console.log(tsp_data)
  for(let i in tsp_data) {
    for(let j in tsp_data) {
      const x = tsp_data[i].x - tsp_data[j].x
      const y = tsp_data[i].y - tsp_data[j].y
      if(!res[i])
        res[i] = []
      // console.log(x,y)
      res[i][j] = Math.sqrt(x*x + y*y)
    }
  }
  // console.log(res[0][1] + res[1][2] + res[2][6] + res[6][7] + res[7][8] + res[8][9] + res[9][4] + res[4][5] + res[5][3] + res[3][0])
  console.log("最短路径序列：0 3 5 4 9 8 7 6 2 1 0")
  console.log("最短路径长：",res[0][3] + res[3][5] + res[5][4] + res[4][9] + res[9][8] + res[8][7] + res[7][6] + res[6][2] + res[2][1] + res[1][0])
  // console.log("最短路径序列：1 2 3 4 6 5 7 8 9 10 11 12 13 14 15 16 17 19 18 20 21 22 23 24 25 28 26 27 29 30")
  return res
}

CalFitness.js

const Copy = require('../Copy.js')

const POP_SIZE = require('./const').POP_SIZE
const CITY_NUM = require('./const').CITY_NUM
const N = require('./const').N

module.exports = function(city,distance) {
  let start,end
  let best = 0
  // 先求每个个体的总路径 city.Distance[i]
  for(let i = 0; i < POP_SIZE; i ++) {
    city.Distance[i] = 0
    for(let j = 0; j < CITY_NUM; j ++) {
      // 获取此路径序列 依次相邻的两个 城市下标
      start = city.colony[i][j]
      end = city.colony[i][j + 1]
      city.Distance[i] +=  distance[start][end]
    }
    // 适应值 = N / 每个个体的总路径
    city.fitness[i] = N / city.Distance[i]
    // 选出最适应者
    if(city.fitness[i] > city.fitness[best])
      best = i
  }

  // best是 最适应者的下标，city.colony[best]
  Copy(city.BestRooting,city.colony[best])
  city.BestFitness = city.fitness[best] // 最优适应值
  city.BestPath = city.Distance[best] // 最优路径长度
  // console.log(city.Distance[best])
  city.BestIndex = best // 最适应者的下标
  // console.log("best",best)
}

Check.js


const CITYNUM = require('./const').CITYNUM
// 检查新生成的节点是否在当前群体中, 0号节点是默认出发的节点
module.exports = function(city,pop,num,r) {
  for(var i = 0; i <= num; i ++) {
    if(r == city.colony[pop][i])
      return true
  }
  return false
}

遗传算法解决TSP问题（Node.js）

参考

TSP问题

问题描述

算法流程

算法目录解析

最优解和实验结果分析

30个城市

10个城市

源代码

data.json

data1.json

Tsp.js

module文件夹

Select.js

Mutation.js

GetFittness.js

Cross.js

Copy

init文件夹

const.js

initColony.js

cityDistance.js

CalFitness.js

Check.js