注:仅为个人学习笔记,内容一定会有不严谨(甚至错误)的地方,内容仅供参考。
另求各路大佬批评指点
幂、并、交、差、相等、包含
-
幂集是子集的集合(当然,也包括空集和它自己,即全集)。 A 的幂集记作 ρ(A),若 A 有 n 个元素,则 ρ(A) 有 2n 个元素;
-
∩、∪均满足幂等、交换、结合、分配、吸收 A∪(A∩B)=A;A∩(A∪B)=A 、德摩根律;
-
两个集合的差:
A−B={x∣x∈A∧x∈/B}
-
集合相等,就是两个集合相互包含
A=B⟺A⊆B∧B⊆A
-
集合包含,就是被包含集合的每个元素都属于包含其的集合
A⊆B⟺∀x∈A,x∈B
环和、环积、笛卡尔积
-
环和,又称对称差,是去掉这两个集合交集的并集。
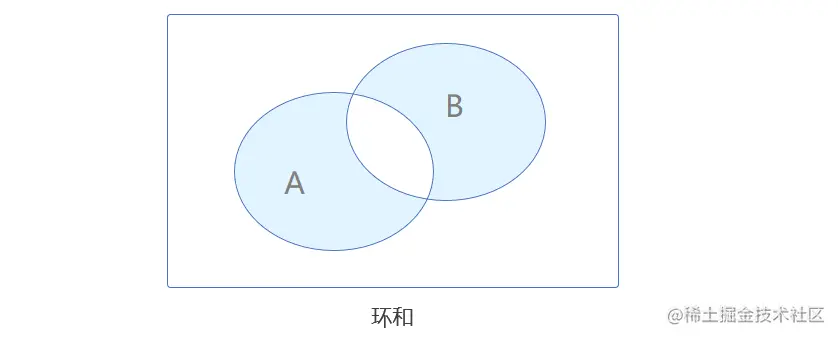
A⊕B=(A−B)∪(B−A)={x∣x∈A∧x∈/B∨x∈B∧x∈/A}A⊕B=(A∪B)−(A∩B)=(A∪B)∩(A∪B)
环和的推论:
A⊕B=A⊕BA⊕B=B⊕AA⊕A=∅
环和满足结合律:(A⊕B)⊕C=A⊕(B⊕C)
交对环和可分配:C∩(A⊕B)=(C∩A)⊕(C∩B)
-
环积(即环和的非)
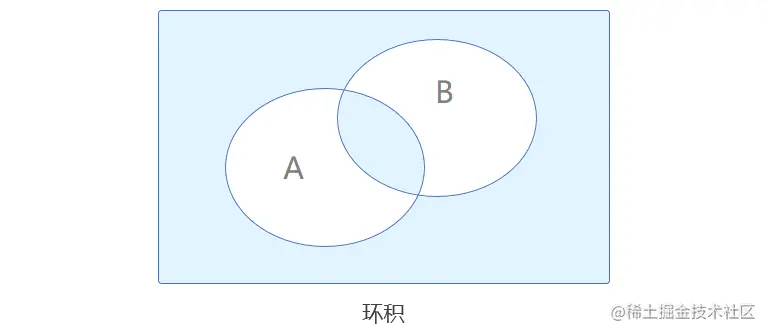
A⊗B=A⊕B
推论:
A⊗B=A⊗BA⊗B=B⊗AA⊗A=U
环积满足结合律:
(A⊗B)⊗C=A⊗(B⊗C)
交对环积可分配:
A∩(B⊗C)=(A∩B)⊗(A∩C)
-
笛卡尔积:
A×B={(x,y)∣x∈A∧y∈B}
例如:A=a,b,B=0,1,2,则:
A×B={<a,0>,<a,1>,<a,2>,<b,0>,<b,1>,<b,2>}B×A={<0,a>,<0,b>,<1,a>,<1,b>,<2,a>,<2,b>}
笛卡尔积不满足交换律,也不满足结合律
A×B=∅,iff.A=∅或B=∅
笛卡尔积对并、交满足分配律,注意顺序!
补充:形如 <a,b> 这样的东西叫做序偶,两个元素按照一定次序组合。
<a,b>=<c,d>,iff. a=c且b=d
势、等势、基数、可数集合、容斥定理
- 集合内所包含元素的个数叫集合的势,势用来度量集合的规模大小;
- 等势:两个集合的势相等。AB 等势记作 A∼B 。 AB 等势则这两个集合中的元素一一对应,要证明则需要在两个集合之间找一个双射的函数。无限集合可以与其子集等势,但有限集合不可能;
- 基数是刻画任意集合大小的概念,集合 A 的基数记作 ∣A∣ ,有限集合的基数就是元素的个数,任意无限可数集合的基数与自然数集的基数相等;
- 可数集合:与自然数集 N 等势的集合,其基数是 ℵ0 (阿列夫零),同时 ℵ0 也是一切可数集合的基数;与实数等势的集合的基数是 ℵ1 ;
- 当集合数量有限时,笛卡尔积的基数等于基数的积,即:
∣A1×A2×⋯×An∣=∣A1∣×∣A2∣×⋯×∣An∣
- 容斥定理
对有限集合A、B,有 ∣A∪B∣=∣A∣+∣B∣−∣A∩B∣,可以推广至多个集合的情况
关于等势、可数集合、不可数集合
两个集合等势,就是这两个集合的势相等,就是这两个集合元素可以一一对应。
- 全体正整数集合和全体正偶数集合等势;
- 全体正整数集合和全体有理数集合等势;
- 全体正整数集合和全体实数集合不等势;
- 等势可传递。
和全体正整数集合等势的集合,称为可数无穷集合。所有可数无穷集合等势;
势比正整数集大的集合称为不可数无穷集合,其中与全体实数等势的不可数无穷集合称为“连续统(continuum)”(可以构造势大于连续统的不可数无穷集合)。所有连续统等势,任何连续统的势都比可数无穷的势要大。
“可数”:既然每一个可数无穷集合中的元素都可以对应到一个正整数,那么就可以用每一个正整数给这每一个元素编号了,也就是可以用正整数来数它们的个数了;
“不可数”:一个直线上的点集是连续统,无论我们怎么设计一个直线上的点编号的方法,我们也无法给所有的点都编号然后来数它们。