离散数学笔记：代数3_同态映射（2）同态的性质、同余关系（补充等价关系）

marsCatXDU_李经纬
2,170 阅读6分钟

笔记内容全部基于西安电子科技大学 鱼亮 老师的 《离散数学II》课堂内容整理

博主数学水平相当一般，内容从数学的角度来看可能相当不严谨甚至存在谬误，仅供参考。

欢迎高人指点

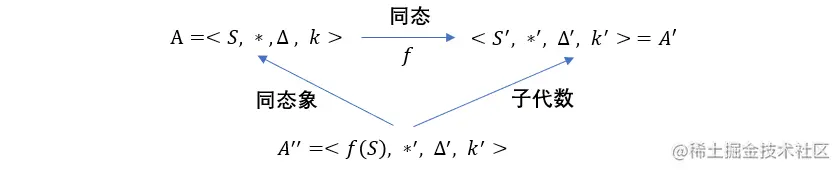
先放一张图，回顾一下同态、同态象、子代数三个概念的关系

定理（同态的性质）

设 ff 是从 A=<S,∗,∘>A=<S, *, \circ> 到 A′=<S′,∗′,∘′>A'=<S', *', \circ '> 的一个同态映射（这里的 ∘、∘′\circ 、\circ ' 都是二元运算，下面的也都是给二元运算用的性质）， A′′=<f(S),∗′,∘′>A''=<f(S), *', \circ '> 是 AA 在同态映射 ff 下的同态象。则有：

  1. 若 ∗* 在 AA 中可交换，则 ∗′*' 在 A′′A'' 中也可交换

  2. 若 ∗* 在 AA 中可结合，则 ∗′*' 在 A′′A'' 中也可结合

  3. 若在 AA 中，∗* 对 ∘\circ 可分配，则在 A′′A'' 中 ∗′*' 对 ∘′\circ ' 可分配

    若说 ∗* 对 ∘\circ 可分配，则 ∗* 在分配律等式括号的外面。如：

    a∗(b∘c)=(a∗b)∘(a∗c) : ∗a*(b\circ c) = (a*b)\circ (a*c) \space :\space * 对 ∘\circ 左可分配

  4. 若 ee 是 AA 中关于 ∗* 的幺元，则 f(e)f(e) 是 A′′A'' 中关于 ∗′*' 的幺元

  5. 若 θ\theta 是 AA 中关于 ∗* 的零元，则 f(θ)f(\theta) 是 A′′A'' 中关于 ∗′*' 的零元

  6. 取 ∀x∈S\forall x \in S，xx 对 ∗* 有逆元 x−1x^{-1} ，则在 f(S)f(S) 中， f(x)f(x) 也有关于 ∗′*' 的逆元 f(x−1)f(x^{-1})

总结来说，就是：原代数中运算的可交换、可结合、可分配都能“保留”到同态象中，原代数中的幺元、零元和逆元，在经过映射后也可以“对应”到同态象中。
上述定理中的前三小条，可用于讨论同态象中二元运算所有的性质

证明：

  1. 证明：
∀a,b∈S，f(a)∗′f(b)=f(a∗b)=f(b∗a)=f(b)∗′f(a) \forall a, b \in S，f(a)*'f(b)=f(a*b)=f(b*a)=f(b)*' f(a)
  1. 证明：
对 ∀a,b,c∈S,f(a)∗′[f(b)∗′f(c)]=f(a)∗′f(b∗c)=f(a∗(b∗c))=f((a∗b)∗c)=f(a∗b)∗′f(c)=[f(a)∗′f(b)]∗′f(c) \begin{aligned} &对\space \forall a,b,c \in S,\\ &f(a)*'[f(b)*'f(c)]\\ =&f(a)*'f(b*c)\\ =&f(a*(b*c))\\ =&f((a*b)*c)\\ =&f(a*b)*'f(c)\\ =&[f(a)*'f(b)]*'f(c) \end{aligned}
  1. 证明：
对 ∀a,b,c∈S,f(a)∗′[f(b)∘′f(c)]=f(a)∗′f(b∘c)=f(a∗(b∘c))=f((a∗b)∘(a∗c))=f(a∗b)∘′f(a∗c)=[f(a)∗′f(b)]∘′[f(a)∗′f(c)]∴∗′对∘′左可分配∵∗′可交换∴[f(b)∘′f(c)]∗′f(a)=[f(b)∗′f(a)]∘′[f(c)∗′f(a)]∴∗′对∘′右可分配∴∗′对∘′可分配 \begin{aligned} &对\space \forall a,b,c \in S,\\ &f(a)*'[f(b)\circ'f(c)]\\ =&f(a)*'f(b\circ c)\\ =&f(a*(b\circ c))\\ =&f((a*b)\circ (a* c))\\ =&f(a*b)\circ' f(a*c)\\ =&[f(a) *'f(b)] \circ' [f(a)*'f(c)]\\ ∴& *' 对 \circ ' 左可分配\\ ∵& *' 可交换\\ ∴& [f(b)\circ'f(c)]*'f(a)\\ =& [f(b) *'f(a)] \circ' [f(c)*'f(a)]\\ ∴& *' 对 \circ ' 右可分配\\ ∴& *' 对 \circ ' 可分配\\ \end{aligned}
  1. 证明：
∵ e∈S∴ f(e)∈f(S)∀a∈S，有：f(a)∗′f(e)=f(a∗e)=f(a)∴ f(e)是A′′中关于∗′的右幺元∵ ∗′可交换∴ f(e)∗′f(a)=f(a)∗′f(e)=f(a)∴ f(e)是A′′中关于∗′的左幺元∴ f(e)是A′′中关于∗′的幺元 \begin{aligned} ∵&\space e\in S\\ ∴&\space f(e)\in f(S) \\ &\forall a\in S，有： \\ &f(a)*'f(e)\\ =&f(a*e)\\ =&f(a)\\ ∴&\space f(e) 是 A'' 中关于*'的右幺元\\ ∵&\space*' 可交换\\ ∴&\space f(e)*' f(a)=f(a)*'f(e)=f(a)\\ ∴&\space f(e) 是 A'' 中关于*'的左幺元\\ ∴&\space f(e) 是 A'' 中关于*'的幺元 \end{aligned}
  1. 证明：
∵ θ∈S∴ f(θ)∈f(S)∀a∈S，有：f(a)∗′f(θ)=f(a∗θ)=f(θ)∴ f(θ)是A′′中关于∗′的右零元∵ ∗′可交换∴ f(θ)∗′f(a)=f(a)∗′f(θ)=f(θ)∴ f(θ)是A′′中关于∗′的左零元∴ f(θ)是A′′中关于∗′的零元 \begin{aligned} ∵&\space \theta \in S\\ ∴&\space f(\theta)\in f(S) \\ &\forall a\in S，有： \\ &f(a)*'f(\theta)\\ =&f(a*\theta)\\ =&f(\theta)\\ ∴&\space f(\theta) 是 A'' 中关于*'的右零元\\ ∵&\space*' 可交换\\ ∴&\space f(\theta)*' f(a)=f(a)*'f(\theta)=f(\theta)\\ ∴&\space f(\theta) 是 A'' 中关于*'的左零元\\ ∴&\space f(\theta) 是 A'' 中关于*'的零元 \end{aligned}
  1. 证明：
由已知条件，得：∀x∈A,有x∗x−1=e∴  f(x)∗′f(x−1)  =f(x∗x−1)  =f(e)∵f(e)是A′′中关于∗′的幺元∴f(x−1)是f(x)的逆元 \begin{aligned} &由已知条件，得：\\ &\forall x\in A,有 x*x^{-1}=e\\ &∴\space \space f(x)*'f(x^{-1})\\ &\space \space = f(x*x^{-1})\\ &\space \space = f(e)\\ &∵f(e) 是 A'' 中关于 *' 的幺元\\ &∴f(x^{-1}) 是 f(x) 的逆元 \end{aligned}

例题

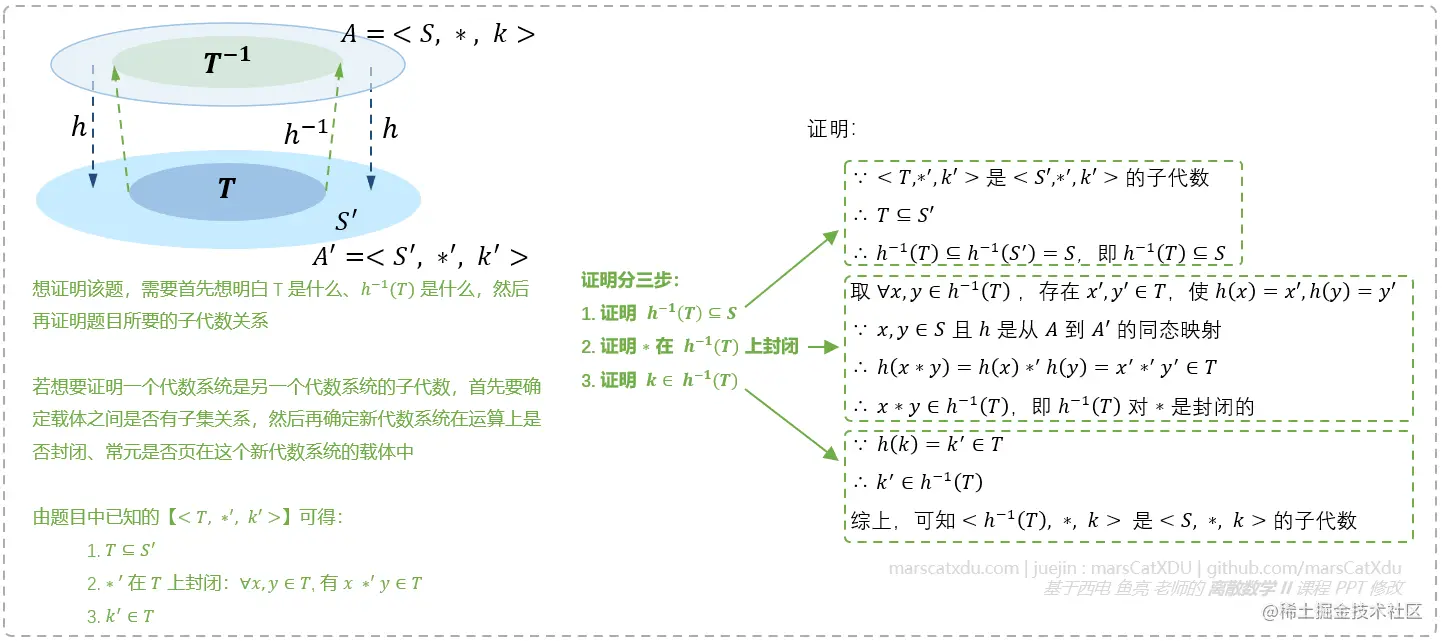
设 hh 是从 A=<S,∗,k>A=<S, *, k> 到 A′=<S′,∗′,k′>A'=<S', *', k'> 的同态映射。请证明：若<T,∗′,k′><T, *', k'> 是 A′A' 的子代数，那么 <h−1(T),∗,k><h^{-1}(T), *, k> 是 AA 的子代数（灰色虚线框内为题解及注释 / 解析，黑色字为正经的解题过程，其他彩色部分均为解析、插图等）

补充：等价关系

等价关系是一个关系，关系也是集合
等价关系满足自反、对称和传递（关系也是一个集合，集合的元素是序偶），对于 aa、bb 等价，一般记作 a∼ba\sim b。

  • 自反：∀a∈A,有a∼a\forall a\in A,有 a\sim a

  • 对称：对 a,b∈Aa, b \in A，若 a∼ba\sim b，则b∼ab\sim a

    即：<a,b>则<b,a><a,b> 则 <b,a>

  • 传递：对 a,b,c∈Aa,b,c\in A，若 a∼b, b∼ca\sim b,\space b\sim c 则 a∼ca\sim c

    即：<a,b>∈R ∧<b,c>∈R⇒<a,c>∈R<a,b>\in R\space \wedge <b,c>\in R \Rightarrow <a,c>\in R

等价关系的有向图的每一分图都是完全图（完全图的每个节点有自回路，每两个节点之间有两条不同方向的边）

等价关系能够对一个集合进行划分，每个划分就是一个等价类。两个元素等价，则它们属于同一个等价类。

元素 aa 关于关系 RR 的等价类，可描述为：{x∣xRa}\{x|xRa\}，记作 [a]R[a]_R，简记为 [a][a] ，其中 aa 被称为该等价类的【表示元素】，等价类的个数被称为【秩】

同余关系

同余关系：设 A=<S,∗,Δ>A=<S, *, \Delta> 是一个代数系统，∼\sim 是 SS 上的等价关系。取 ∀a,b,c∈S\forall a,b,c \in S，则：

  1. 当 a∼ba\sim b 时，若 Δa∼Δb\Delta a\sim \Delta b，则 ∼\sim 在 Δ\Delta 下是 “可保持的” ，称 ∼\sim 是 “关于运算 Δ\Delta 的同余关系”

    aa 和 bb 在运算前属于一个等价类，在运算后又属于一个等价类，两个等价类可能相同也可能不同

  2. 当 a∼b, c∼da\sim b,\space c\sim d 时，若有 a∗c∼b∗da*c\sim b*d ，则 ∼\sim 在 ∗* 下是 “可保持的” ，称 ∼\sim 是 “关于运算 ∗* 的同余关系”

    a∼b, c∼da\sim b,\space c\sim d 意味着 aa、bb 在一个等价类中，cc、dd 在一个等价类中；

    a∗c∼b∗da*c\sim b*d 意味着 a∗ca*c 和 b∗db*d 也在一个等价类中。

    上述的这三个等价类可以是同一个等价类，也可以是完全不同的等价类。

用直白一些的话来讲，如果两个元素【在运算之前就在同一个等价类，运算的结果仍然在同一个等价类】，那么就说这个等价关系对于该运算是同余关系。

下面用图形化的方式来描述一下这个抽象的概念。下图中，每个小格子代表一个等价类（也就是说，位于同一个小格子中的元素属于同一个等价类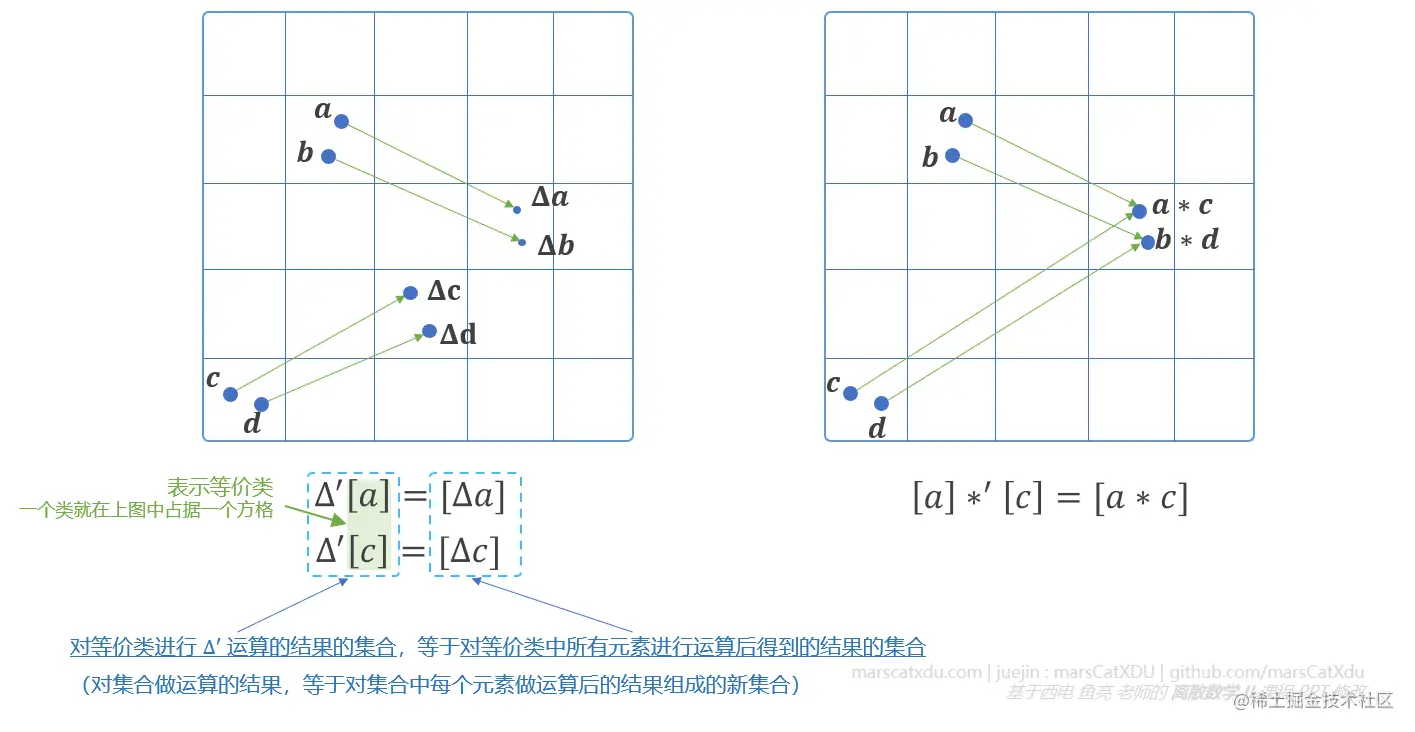） 注意，经过运算后的等价类是可以和运算前元素所在的等价类重合的

证明等价关系关于二元运算是同余关系，有两种方法。一种方法是像上面说的那样，在两个等价关系中各任取两个元素进行运算得到仍在同一等价类中的结果，直接说明同余。另一种是使用三个元素进行说明：取 ∀a,b,c∈S,a∼b\forall a,b,c\in S,a\sim b，若 a∗c∼b∗ca*c\sim b*c 且 c∗a∼c∗bc*a\sim c*b ，则是等价关系是同余关系。

作为样例，下面的例题中会分别用两种方法进行证明。

同余关系证明例题（方法2，用三个元素证明）

例1

将分数定义为整数序偶 <P,Q><P,Q> ，写作 PQ\frac{P}{Q} （Q≠0Q\neq 0）。设 F 是所有分数的集合， ⋅\cdot 和 −- 是普通乘法和一元减法。尝试证明等价关系 ∼\sim 是关于乘法和一元减法的同余关系
证明：
建立 F 上的等价关系：

PQ∼RS⇔PS=RQ\frac{P}{Q}\sim \frac{R}{S}\Leftrightarrow PS=RQ

上面这个等价关系，说的其实是：【“两个分数等价”这件事，等价于两个分数分子分母交叉相乘相等】。
对 ∀a,b,c∈F\forall a,b,c\in F，可以将他们表示为下面的样子：

a=PQ,b=RS,c=TUa=\frac{P}{Q},b=\frac{R}{S},c=\frac{T}{U}

想要证明等价关系是关于运算的同余关系，我们就需要证明【等价关系在该运算下可保持】，也就是证明【在运算之前就在同一个等价类的元素，进行运算后的结果仍然在同一个等价类】。那么我们这里的思路就是，在运算的载体集合中任取两个属于同一等价类的元素，对它们进行运算，得到仍在同一个等价类中的结果即可

我们在这里设运算前就在同一个等价类中的两个元素 a、ba、b 有等价关系 a∼ba\sim b （也就是 PQ∼RS\frac{P}{Q}\sim \frac{R}{S}）。如果我们能证明 对∀c∈F,有ac∼bc对 \forall c\in F, 有 ac\sim bc，也就是证明了【在运算之前就在同一个等价类的元素，进行运算后的结果仍然在同一个等价类】，也就证明了该等价关系 ∼\sim 是关于乘法的同余关系

PQ∼RS⇒PS=RQ⇒PS⋅TU=RQ⋅TU⇒PT⋅SU=RT⋅QU⇒PTQU∼RTSU⇒(PQ)⋅(TU)∼(RS)⋅(TU)\begin{aligned} \frac{P}{Q}\sim \frac{R}{S}&\Rightarrow PS=RQ\\ &\Rightarrow PS\cdot TU=RQ\cdot TU\\ &\Rightarrow PT\cdot SU=RT\cdot QU\\ &\Rightarrow \frac{PT}{QU}\sim \frac{RT}{SU}\\ &\Rightarrow (\frac{P}{Q})\cdot(\frac{T}{U})\sim (\frac{R}{S})\cdot (\frac{T}{U}) \end{aligned}

即

PQ∼RS⇒(PQ)⋅(TU)∼(RS)⋅(TU)\frac{P}{Q}\sim \frac{R}{S}\Rightarrow (\frac{P}{Q})\cdot(\frac{T}{U})\sim (\frac{R}{S})\cdot (\frac{T}{U})

即，当 a∼ba\sim b 时，有 a⋅c∼b⋅ca\cdot c\sim b\cdot c 。又因为乘法可交换，故等价关系 ∼\sim 是关于乘法的同余关系。

对于一元减法的证明，与上面类似：

PQ∼RS⇒PS=RQ⇒−PS=−RQ⇒−PQ∼−RS\begin{aligned} \frac{P}{Q}\sim \frac{R}{S}&\Rightarrow PS=RQ\\ &\Rightarrow -PS=-RQ\\ &\Rightarrow \frac{-P}{Q}\sim \frac{-R}{S} \end{aligned}

即，当 a∼ba\sim b 时，有 −a∼−b-a\sim -b 。故等价关系 ∼\sim 是关于一元减法的同余关系

对于加法的证明，也差不了太多：

PQ+TU∼RS+TU=PU+TQQU∼RU+STSU⇒QU(RU+ST)=SU(PU+TQ)⇒QURU+QUST=SUPU+SUTQ⇒QRU2=SPU2⇒QR=SP⇒PS=RQ⇒PQ∼RS\begin{aligned} \frac{P}{Q}+\frac{T}{U}\sim \frac{R}{S}+\frac{T}{U}=\frac{PU+TQ}{QU}\sim \frac{RU+ST}{SU}&\Rightarrow QU(RU+ST)=SU(PU+TQ)\\ &\Rightarrow QURU+QUST=SUPU+SUTQ\\ &\Rightarrow QRU^2=SPU^2\\ &\Rightarrow QR=SP\\ &\Rightarrow PS=RQ\\ &\Rightarrow \frac{P}{Q}\sim \frac{R}{S} \end{aligned}

例2

给定代数 A=<I,−>A=<I,-> 和 II 上的模 k (k∈I+)k \space (k\in I_+) 关系 ∼\sim ，即 x∼y,iff. x≡y(mod k)x\sim y,\text{iff}. \space x\equiv y(mod \space k) 。请证明 ∼\sim 是关于"−-"运算的同余关系

补充：
定理：模 k 等价，是任何 A⊆IA\subseteq I 上的等价关系。
判定：若 a−b=m⋅ka-b=m\cdot k ，则 aa 与 bb 模 kk 等价，记作 a≡b(mod k)a\equiv b(mod \space k)，其中 k∈I+,m∈Ik\in I^+,m\in I 附：还可以证明模 k 关系是关于 + 、·、一元减法的同余关系

例3

给定代数 A=<I,Δ>A=<I, \Delta >，Δa=a2\Delta a=a^2 . 设 ∼\sim 是 II 上的模 kk 等价关系

∵ a∼b⇔a−b=nk(n∈I)∴ Δa−Δb=a2−b2=(a+b)(a−b)=k⋅n⋅(a+b)即  Δa−Δb=k⋅n⋅(a+b)∴ Δa∼Δb∴ ∼是关于运算Δ的同余关系\begin{aligned} &∵\space a\sim b \Leftrightarrow a-b=nk(n\in I)\\ &∴\space \Delta a-\Delta b = a^2 - b^2=(a+b)(a-b)=k\cdot n\cdot (a+b)\\ &即\space\space \Delta a-\Delta b=k\cdot n\cdot (a+b)\\ &∴\space \Delta a\sim \Delta b\\ &∴\space \sim 是关于运算 \Delta 的同余关系 \end{aligned}

更多例题（方法1，用四个元素证明）

例1

设 ++ 是整数集 II 上的普通加法运算， ∼\sim 是 II 上的模 kk 相等关系（ k∈I+k\in I^+ ），问 ∼\sim 在运算 ++ 上是否是 II 上的同余关系？

例2

设 Δ\Delta 是 II 上的一元运算，取 ∀a∈I,Δa=a2\forall a\in I, \Delta a=a^2 ，∼\sim 是 II 上的模 k(k∈I)k(k\in I) 相等关系，问 ∼\sim 在运算 Δ\Delta 是否是 II 上的同余关系？∼\sim 是否是代数系统 A=<I,+,Δ>A=<I, +, \Delta> 上 AA 的同余关系？

代数系统上的同余关系

设 A=<S,∗,Δ>A=<S, *, \Delta > 是一个代数系统，∼\sim 是载体 SS 上的等价关系。若 ∼\sim 在 AA 上的所有运算下都是可保持的，则称 ∼\sim 是代数系统 AA 上的同余关系。

avatar
文章
阅读
粉丝