Unsupervised Anomaly Detection via Variational Auto-Encoder for Seasonal KPIs in

论文链接：arxiv.org/pdf/1802.03… 关键词：Donut算法

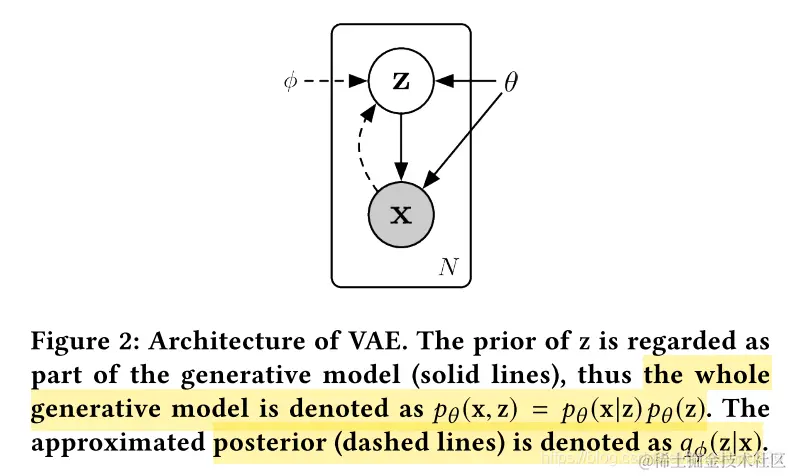
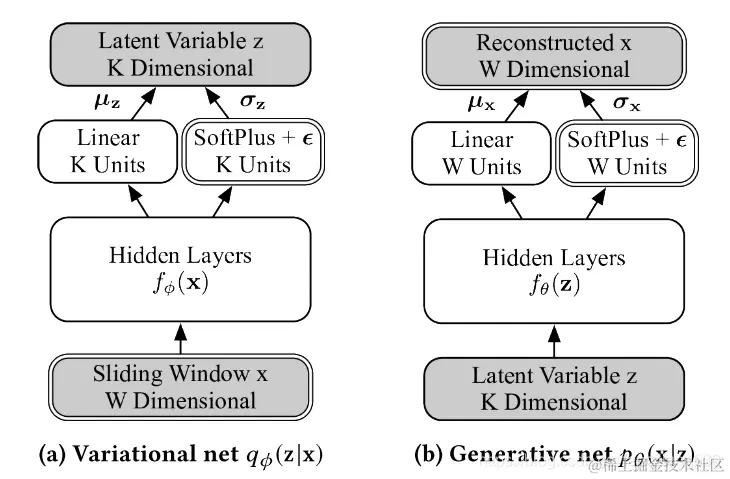
网络结构和随机变量

• prior:
  • z: $p_\theta(z) \sim N(0, I)$
  • x: vector of : $x_{t-W+1},...,x_t$
• posterior:
  • x: $p_{\theta}(x|z) = N(\mu_x, \sigma_x^2 I)$
  • z: $q_\phi(z|x)=N(\mu_z, \sigma_z^2I)$
• hidden features:(通过Hidden Layers--full-connected layer【简单的结构可以更好的解释网络】进行提取）
  • x：$f_\phi(x)$
  • z: $f_\theta(z)$
• Gaussian parameters:(通过hidden feature进行生成）
  • linear layers：
    • $\mu_x=W^T_{\mu_x}f_\theta(z)+b_{\mu_x}$
    • $\mu_z=W^T_{\mu_z}f_\phi(x)+b_{\mu_z}$
  • SoftPlus：(加上一个很小的非负数$\epsilon$）
    • $\sigma_x=SoftPlus[W^T_{\sigma_x}f_\theta(z)+b_{\sigma_x}] + \epsilon$
    • $\sigma_z=SoftPlus[W^T_{\sigma_z}f_\phi(x)+b_{\sigma_z}]+\epsilon$
    • $SoftPlus[a] = log[exp(a)+1]$

模型重构常规模式的步骤：

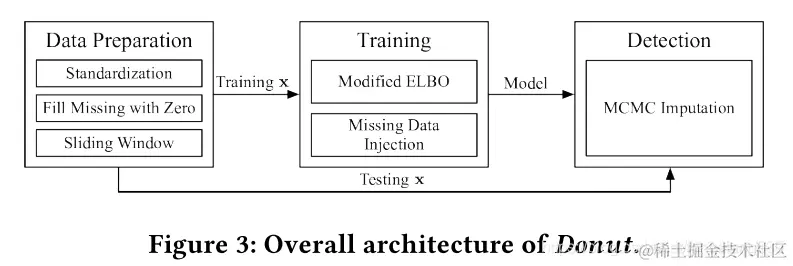
这幅图体现的过程是，通过使用模型，对测试集中有missing points的数据进行重构还原，更具体的细节可以在Bagel算法论文中看到，如下图：

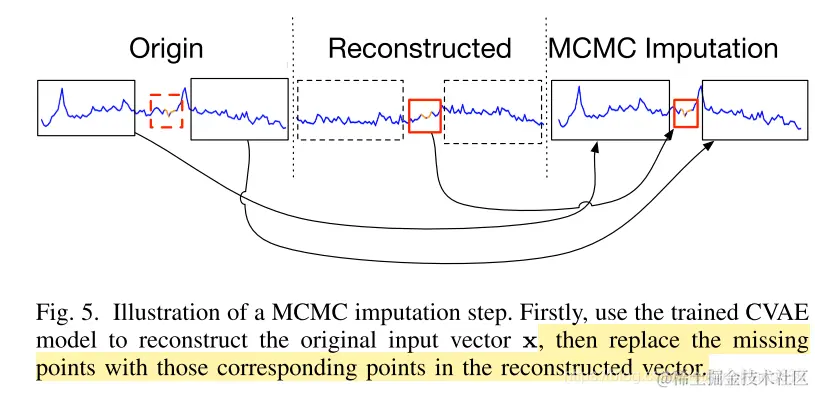
• 在训练过程中，并注入数据填补缺失的内容，而是简单的将其值设置为0
• 上面的数据注入，实在测试集上，仅当模型训练完，才进行缺失数据的注入（使用Donut生成的片段）

训练细节

• SGVB 算法
  • re-paramerterization:
    • 原本： $z \sim N(\mu_z, \sigma^2_zI)$
    • 改为：$\xi \sim N(0, I), \qquad z(\xi)=\mu_z+\xi\cdot\sigma_z$

目标函数：

• $\alpha_w=1时表示x_w不是异常或者缺失点；\alpha_w=0，则表示x_w是非正常点，直接将异常排除$
• $\beta = (\sum^W_{w=1}\alpha_w)/W， 当正常点越多，噪点所起作用也越大$
• 注意到，$\alpha_w$ 其实表示人为的标注，为0的值越多表示人工标注越多，当然如果没有任何标注，算法也能继续运行。这一点使得该算法能很好的处理少量标注的情况
• 函数E的计算方式如下：$E_{q_\phi(z|x)}[x] = \frac{1}{N}\sum^N_i x^i$, N为$q_\phi(z|x)$的样本数