熵，互信息，相对熵

开题词

1948年Shannon博士的《A Mathematical Theory of Communication》（通信的数学理论）横空出世，创世般地开辟了信息论，信息论从此便在通信领域发光发热，为通信工程方面的成功奠定了坚实的理论基础。然而信息论是一门普适性理论，它被认为当下热潮的人工之能和机器学习修炼“内功”，这是因为人工智能本质是处理信息的，本人以为机器学习的算法可以用信息论的思维去理解。有鉴于此，我对学习Information Theory感到期待和对Shannon博士充满敬意，并对不断补充信息论的学者们致以感激。

文章可以看做本人学习信息论的学习笔记（笔记将会以教授知识的形式给出），如有错误，还望大家指正。感谢！

熵（Entropy）

在引入熵的概念之前，我们可以思考这样一个问题：

抛一枚有均匀正反面的硬币，和掷一个均匀六面的骰子，哪一种试验的不确定性更强一点呢？

粗略地看，我们感觉抛硬币这个试验的不确定性会更少一点，因为硬币毕竟仅有2个结果，而骰子有6个结果，但是对于这样一个直觉的事实，我们怎么进行量化从而在数字层面上反映两个随机变量的不确定性的大小关系呢？

Shannon提出了熵的概念，解决了以上这个问题。对于上述离散型随机事件，可以用离散熵定义其不确定性

熵是一个随机变量不确定性的度量，对于一个离散型随机变量 ，其离散熵可以定义为：

其中： 花体 表示为包含所有小 元素的集合，log以2为底。

下面用Shannon离散熵量化解决我们之前引入的两个试验：

设随机变量 为抛一枚均匀硬币的取值，其中正面朝上用 表示，反面朝上用 表示，于是有：
注：由于 概率均相等，为了版面整洁故合并表示。

设随机变量 为掷一个六面均匀骰子的取值，其中 ,于是有：

综上我们有如下结论：

即随机变量 的不确定性确实比随机变量 来的要小，符合我们的直觉。

我们可以更进一步地看，一个随机变量的熵越大，意味着不确定性越大，那么也就是说，该随机变量包含的信息量越大，那到底信息量是什么呢？抛一枚硬币的信息量就是，正面朝上，反面朝上，这2就是信息量；同样，掷骰子的信息量就是6个不同数字的面朝上，这6也是信息量。那么，在计算机角度上看，熵到底是什么，我们不妨看

其实就是意味着，在计算机中，要表示抛硬币的结果，需要用1 bit，要表示掷骰子的结果需要用log6 bit（实际表示时为向上取整3 bit），也就是说**熵是平均意义上对随机变量的编码长度。**为什么这么说呢？

由熵的定义，我们知道：

即，熵实际上是随机变量 的函数 的期望。

至此，我们已经了解到熵在信息论中的意义和在计算机编码中的物理含义。最后我们再说明一下，必然事件的熵是多少呢？应该是0，因为必然是事件是确定无疑的，并不含有不确定性，也就是说，必然事件不含有信息量。

互信息（Mutual information）

熵表明了单个随机变量的不确定程度，那么熵的值是确定不变的吗？我们有办法缩减这个不确定性吗？如果能缩减那缩减多少可以量化吗？

在这里引一句题外话，吴军老师《数学之美》一书曾提到。网页搜索本质正是减少不确定性的一个过程，根据用户的关键字和其他手段减少那些无关搜索，尽量接近用户的搜索意图，这种思维正可以体现信息论的“内功”本色。

我们举一个例子来说明事件不确定性的变化

假设现在我给你一枚硬币，告诉你这是均匀的，请你抛100次然后告诉我结果，结果你抛了100次后，记录的结果是：正面朝上90次，反面朝上10次，你就会开始怀疑“这真是一枚均匀的硬币吗？”

由第一部分熵中，我们知道，这一枚硬币的熵应该是1 bit，但是这样的试验之后，这枚硬币的熵还是1 bit吗？我们可以假设正面朝上的概率为0.9，反面朝上的概率为0.1，计算一下这个熵：

其中， 表示为知道90次正面朝上的事实后，原硬币的熵。

经过抛掷100次后，我们知道这么硬币可能是不均匀的，且新的熵为0.469 bit，也就是说我们在知道90次正面朝上，10次反面朝下的事实之后，这个硬币的熵缩小了0.531 bit，这个0.531的信息量，我们就称为互信息。

从而我们引入互信息的定义：

对于两个随机变量 和 ，如果其联合分布为 ,边缘分布为 ,则互信息可以定义为：

乍一眼看，这个互信息的定义怎么和我们说的例子不太一样，其实这个定义是根据相对熵来下的定义，我们先不用管相对熵，我们看看这个定义能不能变成我们刚刚所说的缩减信息的形式，作如下推导：

经过推导后，我们可以直观地看到 表示为原随机变量 的信息量， 为知道事实 后 的信息量，互信息 则表示为知道事实 后，原来信息量减少了多少。

为了更加形象地描述互信息，请允许我借用互联网上的文氏图来说明：

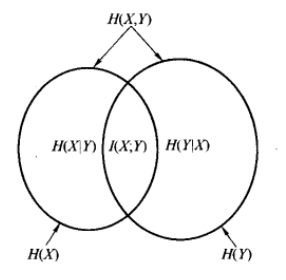
最后，如果随机变量 独立，那么互信息是多少呢？应该是0，这意味着，知道事实 并没有减少 的信息量，这是符合直觉的因为独立本来就是互不影响的。

相对熵

根据上面的叙述，我们了解到信息论中，对于孤立的一个随机变量我们可以用熵来量化，对于两个随机变量有依赖关系，我们可以用互信息来量化，那么对于两个随机变量之间相差多少？也就是说，这两个随机变量的分布函数相似吗？如果不相似，那么它们之间差可以量化吗？

相对熵就是回答以上的问题，它给出了两个分布之间的差异程度的量化，也就说相对熵代表的是这个两个分布的“距离”。

我们引入相对熵的定义：

两个概率密度函数 和 之间的相对熵定义为：

相对熵的一个应用场景就是，假设某一个样本服从分布 ，我们通过样本拟合出来的分布是 ,那么他们之间的差异程度就是 ，再一步而言， 根据分布 我们得出表示随机变量的码长为其熵 （该表达等价于 ），而我们估计的分布为 ,那么他们的关系可以表达为：

这样我们就量化了两个分布之间的“距离”了。

最后，我们解决互信息定义时候留下的疑团：

由这样的推导，我们知道互信息本质上其实是描述了联合分布 ，与两个边缘分布之积 的差异程度，如果差异程度为0，表示两个随机变量独立，符合我们的直觉。

转载自：zhuanlan.zhihu.com/p/36192699