3.2 Processing实用调色教程：HSB模式与颜色插值

忘荃
1,981 阅读5分钟

前一篇文章中介绍了关于Processing中颜色的灰度表示法，颜色透明度，以及RGB彩色表示，然而还有一些关于颜色的常用技巧，这些技巧主要是在需要颜色在时间或者空间上产生渐变的时候使用。如果你有相关的使用需求，那么不妨现在开始这新一部分的颜色学习吧：

RGB表示法的问题

我们先从下面这个绘制一堆颜色渐变的多个矩形的程序开始说起：

def setup():
    size(500, 500)
    N = 50
    stroke(0)
    for i in range(N):
        for k in range(N):
            fill(i*5, k*5, 30) # 为每个格子设置填充色
            rect(i*10, k*10, 10, 10)
12345678

效果：
在这里插入图片描述

表面上看上去没什么问题，在RGB颜色的表示中，我们的矩形越向右边，R（red）值就越大，而越向下，G（green）值就越大，这样使用RGB表示和循环相结合的方式，就可以画出空间上的颜色渐变。但是，这样真的没问题吗？

并不是，仔细观察后你会发现，越靠近左上角，颜色就越“阴暗”，而越靠近右下角，颜色就越“明亮”，这样就会导致对不同位置的突出程度不一样，然而我们有些时候想要的是一种各个颜色之间“不同但平等”的效果。下面我们就解决这个问题。（在上面的程序中调大B值能够部分缓解这个问题，但是无法根本解决，有兴趣可以自行尝试~）

HSB彩色表示格式

程序例子

同样的程序，这次我们使用HSV格式进行颜色设置：

def setup():
    size(500, 500)
    colorMode(HSB)
    N = 50
    stroke(0)
    for i in range(N):
        for k in range(N):
            fill((i-k+30)*2, 200, 200) # 为每个格子设置填充色
            rect(i*10, k*10, 10, 10)
123456789

效果：

嘻嘻
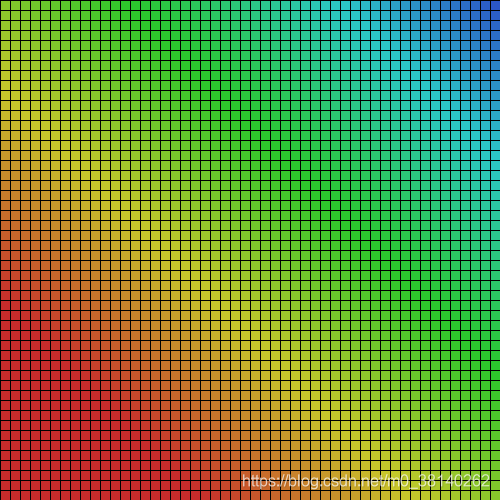
可以看到，在颜色设置格式从RGB改变成HSB后，我们仍旧尽量保持了颜色渐变方式和前面的一致（从右下角到右上角的颜色渐变）。这个时候，我们惊喜地发现，各个颜色之间“不平等”的问题被我们解决啦~

那么，HSB格式到底是何方神圣呢？

色相

HSB其实也是三个单词的缩写，分别代表了：色相，饱和度，亮度。通过单一地改变色相，就能够得到红蓝绿在内的多种颜色：
色相值在Processing中的取值是从0到255的值，如果将其转换为0-360的度数表示，就可以得到下面的结果（色相轮）：
在这里插入图片描述
现在，这里的色相轮忽略了颜色的深浅，明亮，丰富或苍白。只知道要找到色相，请考虑色轮上最接近的任何颜色。

（“但是黑色？白色？灰色吗？” –稍等，天才。我们一会儿会到达那里的。）

如果您想对HSB有一个直观的了解，则应牢记几个锚点。我使用红色，绿色和蓝色，因为它们在圆上等距分布：

红色为0°
绿色为120°
蓝色为240°
红色也是360°，与0°时候的效果完全相同

因此，当我考虑添加什么颜色时，只要考虑一下这三个点，就可以快速键入一个使我非常接近正确色相的数字。

饱和度

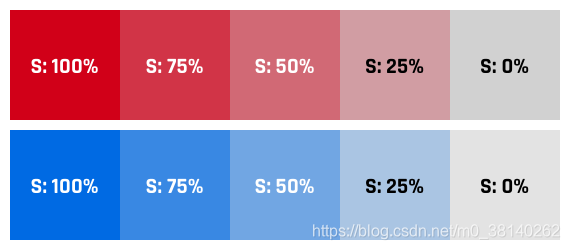
饱和度是介于0到100之间的数字。因此，无论您选择了哪种色调，饱和度为100％将是该颜色的最丰富版本：
在这里插入图片描述

亮度

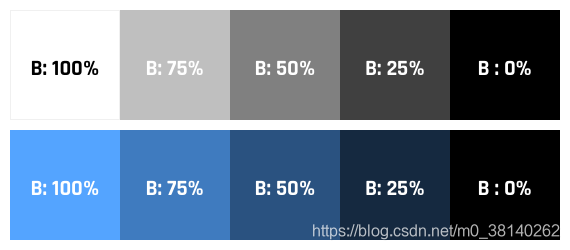
亮度是介于0到100之间的数字。像饱和度一样，它有时以百分比表示。就其含义而言，这一点相当明显，但是有一个快速的认识。

0％的亮度是黑色，无论色相还是饱和度。

仅当饱和度也为0％时，100％的亮度才为白色。否则，100％的亮度只是一种……非常明亮的颜色。

听起来令人困惑？这样想吧。想象亮度是一个灯泡。0％表示灯泡熄灭（房间内的灯黑）。100％表示光线已满。因此，100％的亮度是较为明亮的颜色，而如果光线已经是白色，则100％的亮度是纯白色。
在这里插入图片描述

HSB总结

因此，在HSB格式中，我们可以用三个有意义的数字的组合来描述一种颜色：

  • 色相：色轮中对应位置的颜色
  • 饱和度：注入颜色的方式
  • 亮度：“灯泡”打开的程度

在Processing中，这三个值都是0到255（重要的从来不是取值范围，而是值之间的相对大小）。

通过改变色相的值，我们可以产生颜色的渐变；而改变饱和度或者亮度，则能够通过颜色表达一个形状的重要或者是不重要。

另一种方式控制渐变色：颜色插值

有时候，你想要的并不是那种彩虹色一样的颜色大集合式渐变，而是一种在一个更狭小的颜色范围内变化的渐变，这个时候，你可以从前面的HSB模式中，将色相值控制在一个较小的范围内实现这样的效果。

而另外一种效果则是颜色插值，也就是确定颜色渐变的两个渐变端点的颜色，然后根据插值确定中间颜色：

def setup():
    size(500, 500)
    N = 50

    fromC = color(204, 102, 0) # 插值的起始颜色，RGB表示
    toC = color(0, 153, 153) # 插值的终止颜色

    stroke(0)
    for i in range(N):
        for k in range(N):
            tmpC = lerpColor(fromC, toC, 1.0/60*(i-k+30)) # 颜色插值产生渐变
            fill(tmpC)
            rect(i*10, k*10, 10, 10)
12345678910111213

效果：
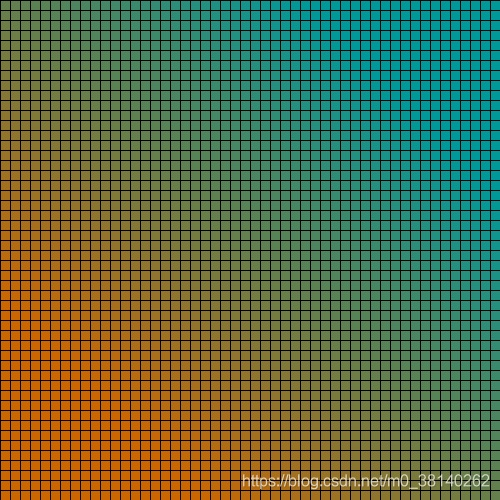
在这里插入图片描述

相关作品欣赏

最后，不妨一起来欣赏一个使用颜色渐变的Processing动态几何作品：
作品链接
作品截图：
在这里插入图片描述

avatar
文章
阅读
粉丝