1/什么是正态分布?
正态分布(Normal Distribution),也被称为高斯分布,代表着概率的分布情况(代表着某一个样本落在某个区域的概率大小),是统计学中的一个重要概念。
在科学理论不甚发达的过去,早期科学家们往往先从观察事物现象开始,发现、记录并试图归纳、总结,最后抽象出背后的规律。
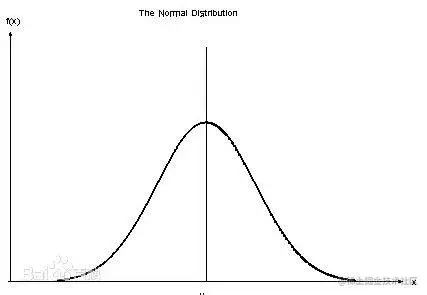
当一组数据或样本涉及到“平均”和“偏差”时,它们出现的频率往往会被描绘成下面这条曲线:
<1> 图中横轴代表着样本值的大小,纵轴则是该样本值出现的概率,其中这条曲线即正态分布曲线。
<2> 当某个样本值x出现的次数更多的时候,代表它出现的概率更大,所以它所对应的y轴的曲线就会鼓起来,就会更高,成为一个峰
2/ 正态分布图中一些概念的解释
观察这个图形,正态曲线呈现出“钟”形,以 x=μ (均数所在的位置)为中心左右对称。随着x变得无穷大或者无穷小,对应的y横轴无穷接近,合成的面积为1,代表所有样本出现的概率之和为 100%。
公式中包含两个参数,期望(均数)μ 和标准差 σ。
我们也常用更简化的形式描述什么是正态分布N(μ,σ^2):
μ 均值,代表着分布的集中趋势,横轴上离 μ 越接近的值,出现的概率越大;
σ^2 方差:代表数据分布的离散程度,σ 越大,数据分布越分散,曲线越“矮胖”,有点类似于股票中的筹码分布图
标准差越大,曲线越矮胖
标准差越小,曲线月高瘦
3/ 现实中的事例
事实上,生活中,或者自然界中,很多数据都是符合正态分布的,这是很巧妙的一种情况。
<1> 比如一群人的身高或脚的大小,
<2> 我每天上班所需要的时间,
<3> 一个班级里所有学生的语文成绩。
<4> 公司内员工的绩效
<5> 公司内员工的工时数据,大多数员工集中在9:50左右,极个别的员工更早来公司,极个别的员工更晚来公司
其背后的理论支撑叫做中心极限定理。我个人觉得这有点类似于中国的中庸之道。绝大多数人都是很平庸的,集中在中间部位,只有极个别的人是比较极端的。
4/ 了解了什么是正态分布,对我们有什么用呢?
你可以试着找到现实生活中类似“上班时长”的重复随机事件,记录不同的情况出现的次数,统计频率并描绘成图(Excel 就可以轻松实现),检查下它的形状,是否接近正态分布。
当你积累足够多的数据,出现某种“神秘”的规律特征后,未发生的事件会大概率落在一个可信的区间内。
相信读到这里,你已经大致了解了什么是正态分布,并可以在生活中发现它的存在,并利用它来“预测未来”。
5/ 如何判定一组数据是否符合正态分布
有2种方法可以检验数据是否符合正态分布:
<1> ks检验
特点是比较严格,基于的原理是CDF,理论上可以检验任何分布,所以需要在参数中指定需要进行哪种分布的验证
from scipy import stats
import pandas as pd
import numpy as np
data_df = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
mean_value = data_df['value'].mean()
std_value = data_df['value'].std()
print( stats.kstest(data_df['value'],"norm") )
得到的结果为:KstestResult(statistic=0.03071564611208749, pvalue=0.29694403078200393)
p>0.05,说明是正态分布
<2> Shapiro检验
专门用来检验正态分布,但是该函数不适用于样本量>5000的情况,如果样本量>5000,则会有warning提示
import pandas as pd
import numpy as np
from scipy.stats import shapiro
data_df = pd.DataFrame(np.random.randn(1000)+10,columns = ['value'])
mean_value = data_df["value"].mean()
std_value = data_df["value"].std()
print( shapiro(data_df) )
得到结果为:(0.9962895512580872, 0.017624640837311745)
