T检验

作用：
    根据某个条件，把原始数据集分成2部分，然后分析这2部分数据在某个变量上否存在显著差异，其实就是想看某个条件是否能让2组人在某个变量上产生差别
    有点类似于高中生物中学习的实验组和对照组的区别是否显著
    其实就是想看看，某种做法是否能产生作用。

场景：
    分析有房补和没有房补的员工，月均工时是否存在显著差异。管理者想看看有房补的员工，月均工时是否更长。
    进行t检验，会得到2个值，一个是t，另一个是pvalue
    我们先要关注的是pvalue值，有的地方也叫sig值，如果pvalue<0.05，说明2组数据有显著差异，然后在看2组样本的均值，根据均值的大小知道哪一组更好。
 
 代码：
   from scipy import stats

   stats.ttest_1samp(data,1)     # 单样本t检验
   stats.ttest_rel(data1,data2)  # 配对样本t检验，必须是一对一的，
   stats.ttest_ind(data1,data2)  # 独立样本t检验，不需要2个样本集的数量相同
   
 ###################################################################################################
 ###################################################################################################
 01.概念
    T检验是通过比较不同数据集合的均值，研究两组数据之间是否存在显著差异。
    
 02.分类
    不同的T检验方法适用于不同的分析场景，具体的分类如下：
    单样本t检验： 与某个数字对比，是否有显著差异
    配对样本t检验：配对数据差异，是否显著
    独立样本t检验：2组数据的差异

 03.t检验的前提条件
    无论是单样本T检验、配对样本T检验还是独立样本T检验，都有几个基本前提：
      （1）T检验属于参数检验，用于检验定量数据（数字有比较意义的），也就是说是用来检验数值型数据的，不能用来检验离散型数据，若数据均为定类数据则使用非参数检验。
      （2）样本数据服从正态或近似正态分布，若不满足，则可考虑使用非参数检验。
      （3）T检验的前提是服从正态分布，大样本是可以的，一般样本量大于30就算大样本。
          补充：一般来说，如果两列数据每列数字的个数超过30个，可以默认其均值服从正态分布，可以直接用t检验。
                因为在大样本（>30就是大样本）情况下，有中心极限定理保证你的正态性。
                问:想请教一下各位大神，样本量大概有9000多，但是不符合正态分布的一组数据可以使用t检验吗？
                答：<1> 中心极限定理和大数定理，给你可以用t检验的证据，除非你的数据本身是时间序列，又不平稳，那就另说了
                   <2> t检验是可以的，因为在大样本情况下，有中心极限定理保证你的正态性。
      
 04. 案例应用
    （1）单样本t检验
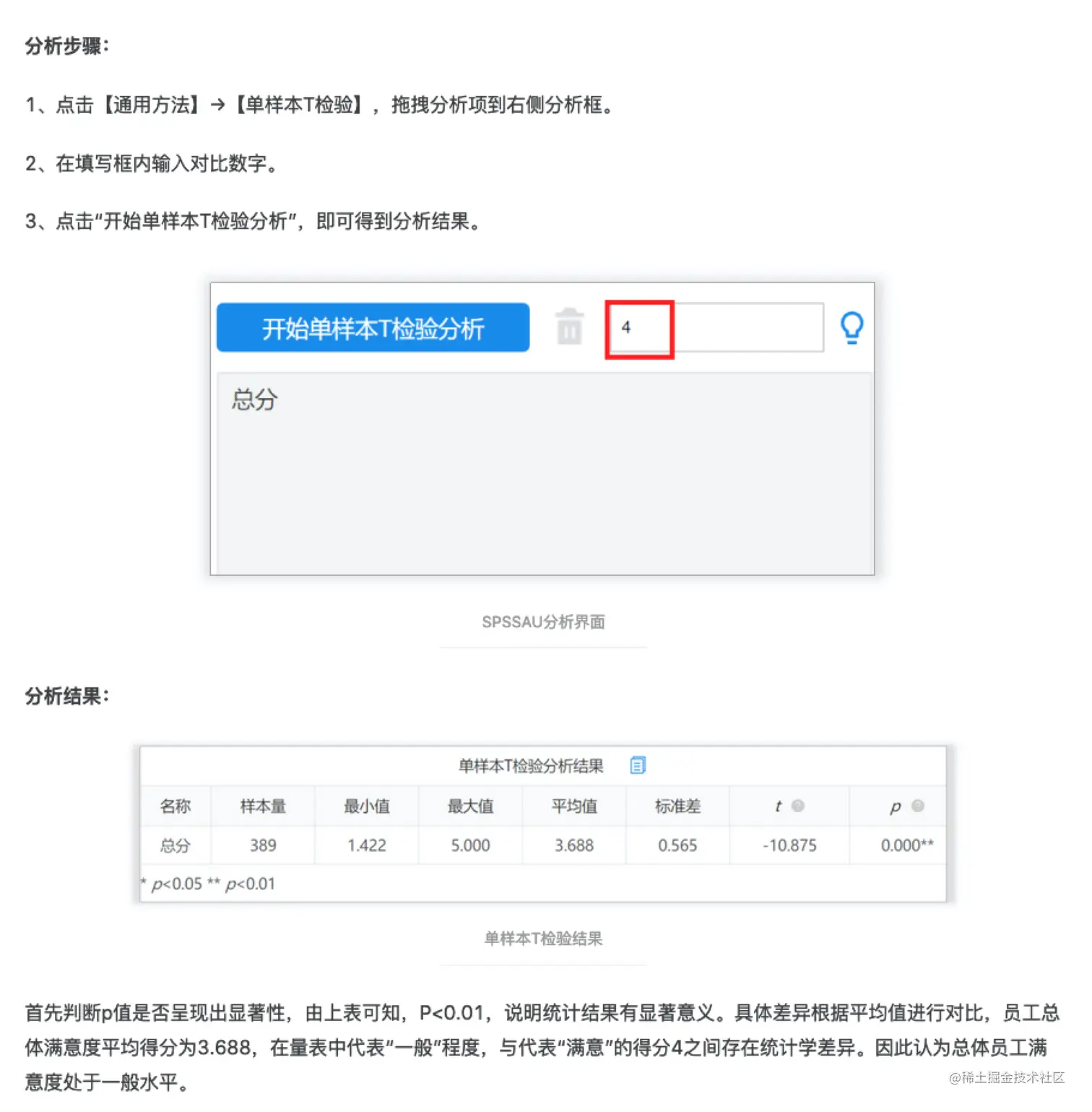
         单样本T检验用于比较一组数据与一个特定数值之间的差异情况。
         比如，某公司用五级李克量表的调查问卷进行员工满意度调查，其中‘4分’代表满意，分析人员可通过单样本t检验了解员工总体满意程度与“满意”（4）之间是否有明显差异。

    （2）配对样本T检验
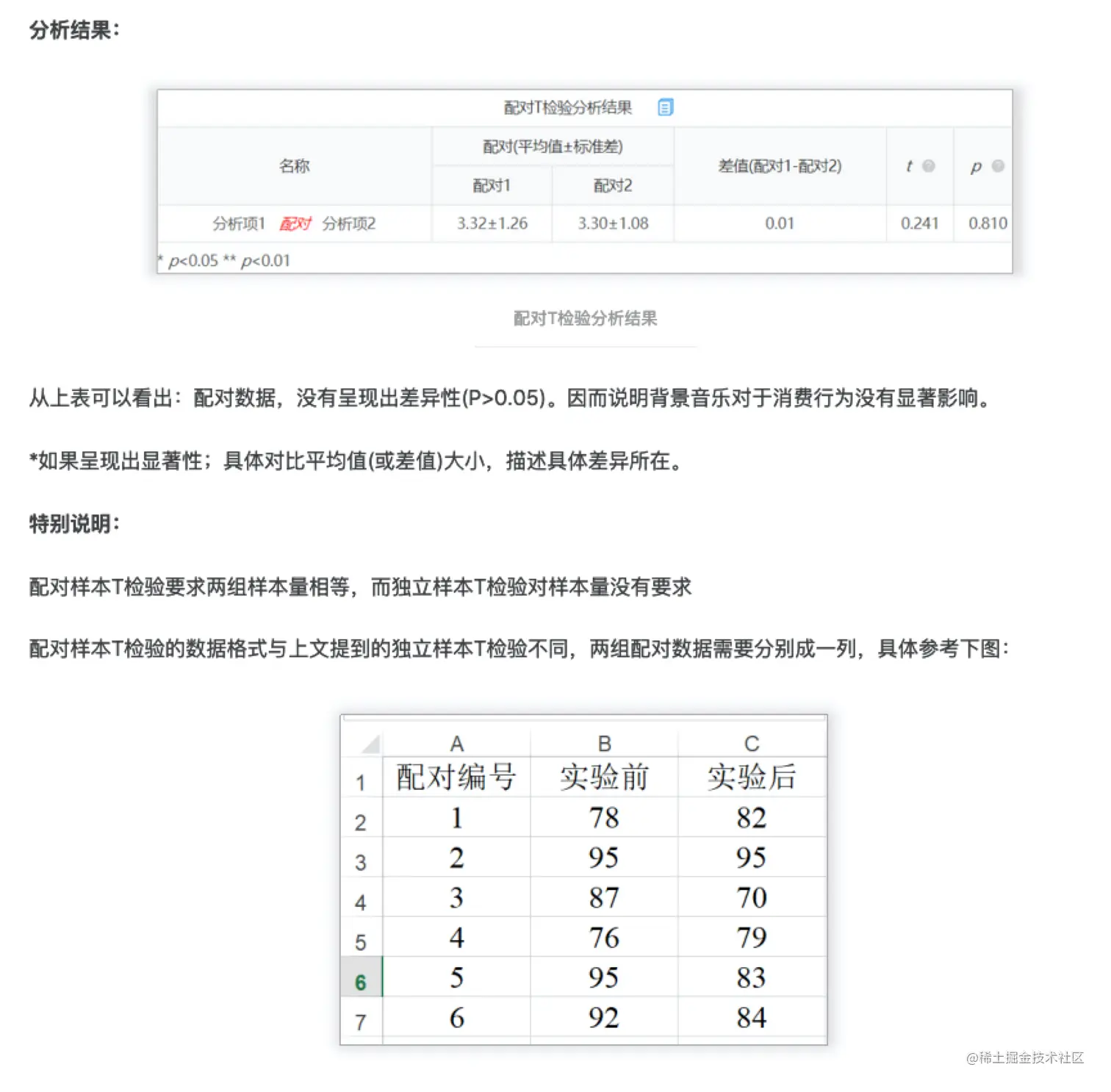
         用于分析配对定量数据之间的差异对比关系。与独立样本t检验相比，配对样本T检验要求样本是配对的，两个样本的样本量要相同；样本先后的顺序是一一对应的。
         案例：比较在两种情况下(有背景音乐和无背景音乐)；顾客的购买意愿是否有着明显的差异性。通过两组数据的对比分析，判断背景音乐是否会影响顾客的消费行为。

    （2）独立样本T检验（T检验）
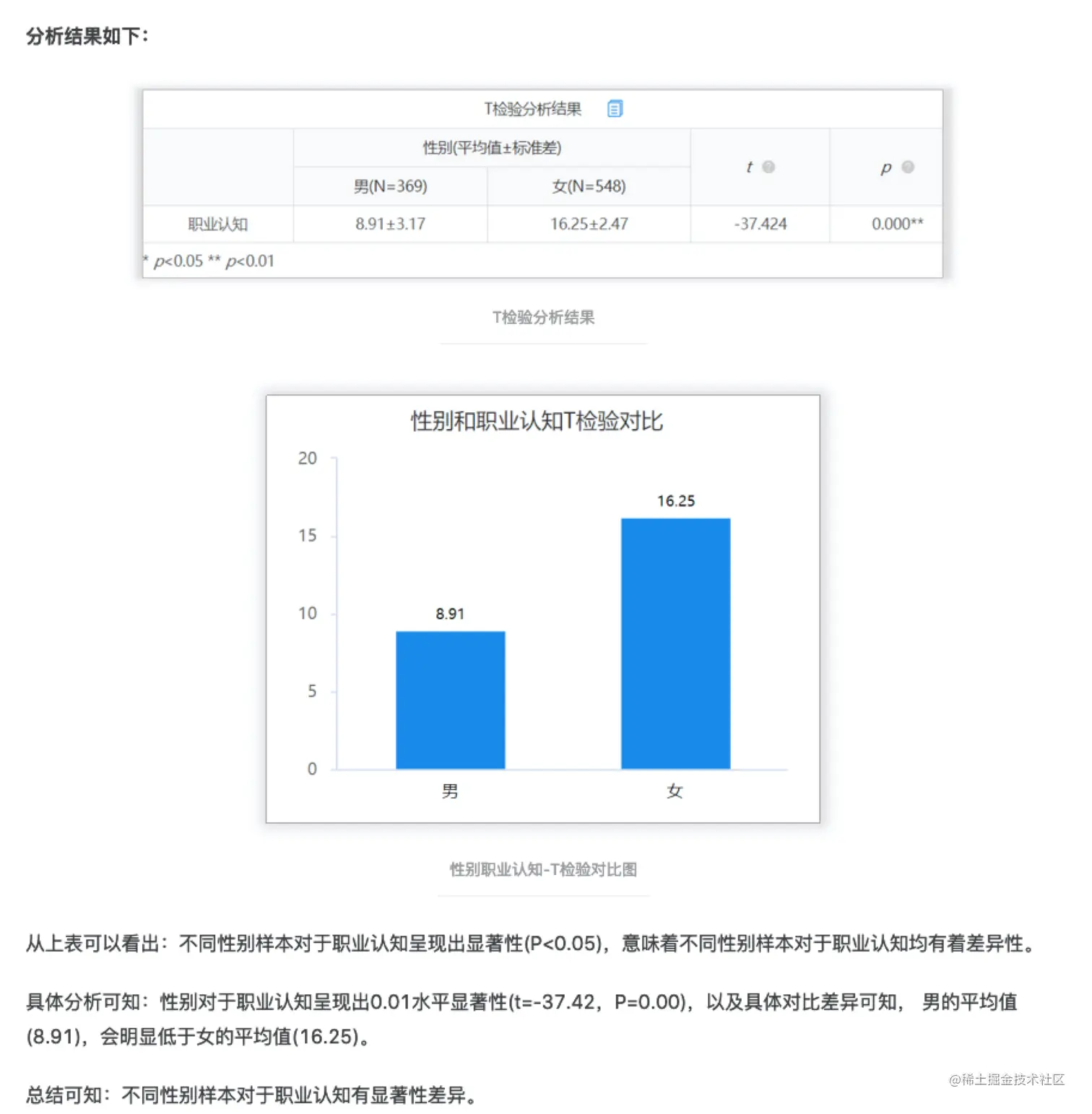
        独立样本T检验用于分析定类数据（X）与定量数据（Y）之间的差异情况。
        独立样本T检验除了需要服从正态分布、还要求两组样本的总体方差相等。当数据不服从正态分布或方差不齐时，则考虑使用非参数检验。
        案例：比较男生与女生的职业认知得分是否存在显著差异，可采用独立样本T检验进行分析。