Chapter3 列表List与选择排序、插入排序、归并排序对于向量这种采用静态储存策略的结构可以使用循秩访问进行高效静

3.1 从向量到列表

3.1.1 从静态到动态

操作方式可以根据是否修改数据结构分为两类

静态：仅读取，数据结构的内容和组成一般不变：get()，search()

动态：需写入，数据结构将整体或局部发生改变：insert(),remove()

对应地，数据元素的存储与组织方式也分为两种

静态：数据空间整体创建和销毁

数据元素的物理存储次序和其逻辑次序严格一致，支持==高效静态操作==：向量

动态：为各数据元素动态分配和回收物理空间

相邻元素记录彼此物理地址，在逻辑上形成一个整体，支持==高效动态操作==：列表

3.1.2 由秩到位置

对于向量这种采用静态储存策略的结构可以使用循秩访问进行高效静态操作，如下面重载下标运算符的复杂度为O(1)，可以把这种访问方式比作快递员根据地址直接送货上门。RAM的访问方式就是循秩访问

template <typename T>
T &Vector<T>::operator[](Rank r) //重载下标运算符
{
    return _elem[r];
    // assert: 0 <= r < _size
}

而像列表这种采用动态储存策略的结构也可以使用循位置访问，即利用节点之间的相互引用找到特定节点，但是复杂度高达O(n)。可以把这种访问方式比作通过我的朋友A的亲戚B的同事C的...的同学Z来访问Z。TM（图灵机）的访问方式就是循位置访问，只能亦步亦趋地到达想要到达的位置。

template <typename T>
T &List<T>::operator[](Rank r) const
{
    ListNodePosi(T) p = first(); //从首节点出发
    while (0 < r--)
        p = p->succ; //顺数第r个节点即是
    return p->data;  //返回目标节点所存元素
}

3.1.3 列表概述

L=\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}

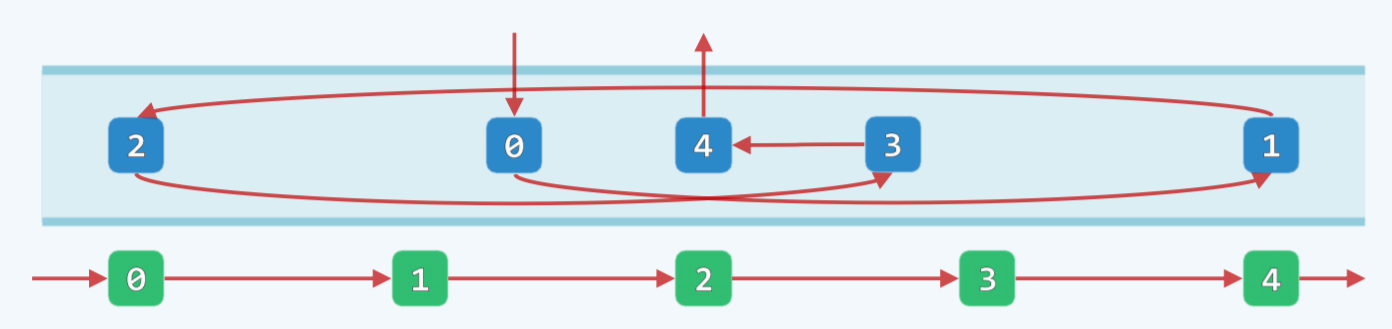
列表是具有线性逻辑次序的一组元素构成的集合，是链表结构的一般化推广，其中的元素称为节点(node)，通过引用或指针彼此联结。相邻节点彼此互称为前驱(predecessor)或后继(successor)（每个元素若有前驱或后继则都是唯一的），没有前驱或后继的节点称为首节点(First Node)或末节点(Last Node)，它们都是可见的，而首节点前有header(头节点)，末节点前有trailer(尾节点)，header和trailer是不可见的。

可以等效地理解header/first node/last node/trailer的Rank为-1 / 0 / n-1 / n

3.2 接口

3.2.1 列表节点

每个节点都存有数据对象data，在不产生歧义的前提下我们不区分node和其对于的data对象，此外，每个节点设置指针pred和succ分别指向其前驱和后继。

创建一个列表节点对象需提供参数以设置各个变量，其中pred和succ若未指定则默认取作NULL

定义各ADT接口如下：

//ListNode模板类
typedef int Rank;                     //秩
#define ListNodePosi(T) ListNode<T> * //列表节点位置(指针)

template <typename T>
struct ListNode //列表节点模板类（双向链表形式实现）
{
    //成员
    T data;               //当前节点所存数据对象
    ListNodePosi(T) pred; //当前节点前驱节点位置
    ListNodePosi(T) succ; //当前节点后继节点位置
    //构造函数
    ListNode() {} //针对header和trailer的构造
    ListNode(T e, ListNodePosi(T) p = NULL; ListNodePosi(T) s = NULL)
        : data(e), pred(p), succ(s) {} //默认构造器
    //操作接口
    ListNodePosi(T) insertAsPred(T const &e); //紧靠当前节点之前插入新节点
    ListNodePosi(T) insertAsSucc(T const &e); //紧靠当前节点之后插入新节点
};

3.2.2 列表

ADT接口

列表ADT支持的操作接口

操作接口	功能	适用对象
`size()`	报告列表当前的规模（节点总数）	列表
`first() last()`	返回首、末节点的位置	列表
`insertAsFirst(e) insetAsLast(e)`	将`e`当作首、末节点插入	列表
`insertBefore(p, e) insertAfter(p, e)`	将`e`当作节点p的直接前驱、后继插入	列表
`remove()`	删除位置p处的节点，返回其数值	列表
`disordered()`	判断所有节点是否已按非降序排列	列表
`sort()`	调整各节点的位置，使之按非降序排列	列表
`find(e)`	查找目标元素`e`，失败时返回`NULL`	列表
`search(e)`	查找目标元素e，返回不大于e且秩最大的节点	有序列表
`deduplicate()`	剔除重复节点	列表
`uniquify()`	剔除重复节点	有序列表
`travserse()`	遍历并统一处理所有节点，处理方法由函数对象指定	列表

List模板类

#include "listNode.h"

template <typename T>
class List //列表模板类
{
private:
    int _size;               //规模
    ListNodePosi(T) header;  //头哨兵
    ListNodePosi(T) trailer; //尾哨兵

protected:
    void init();                                                         //列表创建时初始化
    int clear();                                                         //清除所有节点
    void copyNodes(ListNodePosi(T), int);                                //复制列表中自位置p起的n顷
    void merge(ListNodePosi(T) &, int, List<T> &, ListNodePosi(T), int); //有序列表区间归并
    void mergeSort(ListNodePosi(T) &, int);                              //对从p开始连续的n个节点归并排序
    void selectionSort(ListNodePosi(T), int);                            //对从p开始连续的n个节点选择排序
    void insertionSort(ListNodePosi(T), int);                            //对从p开始连续癿n个节点插入排序

public:
    //构造函数
    List() { init(); }                     //默认
    List(List<T> const &L);                //整体复制列表L
    List(List<T> const &L, Rank r, int n); //复制列表L中自第r项起的n项
    List(ListNodePosi(T) p, int n);        //复制列表中自位置p起的n顷
    //析构函数
    ~List(); //释放(包括header，trailer在内的)所有节点
    //只读访问接口
    Rank size() const { return _size; }                    //返回规模
    bool empty() const { return _size <= 0; }              //判空
    T &operator[](Rank r) const;                           //重载，支持循秩讵问（效率低）
    ListNodePosi(T) first() const { return header->succ; } //首节点位置
    ListNodePosi(T) last() const { return trailer->pred; } //末节点位置
    bool valid(ListNodePosi(T) p)                          //判断位置p是否对外合法
    {
        return p && (trailer != p) && (header != p);
    }                                      //将头、尾节点等同亍NULL
    int disordered() const;                //判断列表是否已排序
    ListNodePosi(T) find(T const &e) const //无序列表查找
    {
        return find(e, _size, trailer);
    }
    ListNodePosi(T) find(T const &e, int n, ListNodePosi(T) p) const; //无序区间查找
    ListNodePosi(T) search(T const &e) const                          //有序列表查找
    {
        return search(e, _size, trailer);
    }
    ListNodePosi(T) search(T const &e, int n, ListNodePosi(T) p) const;     //有序区间查找
    ListNodePosi(T) selectMax(ListNodePosi(T) p, int n);                    //在p及其前n-1个后继中选出最大者
    ListNodePosi(T) selectMax() { return selectMax(header->succ, _size); }  //整体最大者                                                                         // 可写讵问接口
    ListNodePosi(T) insertAsFirst(T const &e);                              //将e当作首节点揑入
    ListNodePosi(T) insertAsLast(T const &e);                               //将e当作末节点揑入
    ListNodePosi(T) insertBefore(ListNodePosi(T) p, T const &e);            //将e当作p的前驱揑入
    ListNodePosi(T) insertAfter(ListNodePosi(T) p, T const &e);             //将e当作p的后继揑入
    T remove(ListNodePosi(T) p);                                            //删除合法位置p处的节点,返回被删除节点
    void merge(List<T> &L) { merge(first(), size, L, L.first(), L._size); } //全列表归并
    void sort(ListNodePosi(T) p, int n);                                    //列表区间排序
    void sort() { sort(first(), _size); }                                   //列表整体排序
    int deduplicate();                                                      //无序去重
    int uniquify();                                                         //有序去重
    void reverse();                                                         //前后倒置（习题）                                                                        // 遍历
    void traverse(void (*)(T &));                                           //遍历，依次实施visit操作（函数指针，叧读或局部性修改）
    template <typename VST>                                                 //操作器
    void traverse(VST &);                                                   //遍历，依次实施visit操作（函数对象，可全局性修改）
};

3.3 无序（常规）列表

3.3.2 默认构造方法

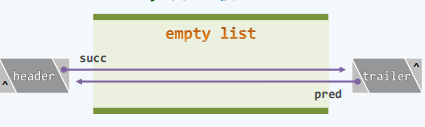
创建List对象时，默认构造方法就是调用init()，在列表内部创建一对头、尾哨兵节点，并适当设置其前驱、后继指针构成一个双向链表。

template <typename T>
void List<T>::init() //列表初始化，在调用列表时统一调用
{
    hearder = new ListNode<T>; //创建头哨兵节点
    trailer = new ListNode<T>; //创建尾哨兵节点
    header->succ = trailer;	//互联
    header->pred = NULL;	//互联
    trailer->pred = header;	//互联
    trailer->succ = NULL;	//互联
    _size = 0; //记录规模
}

3.3.4 查找

在==p==（可以是trailer）的==n==个前驱（这也是为何在参数列表中我们设定n在p前面）中（不包括p）查找等于==e==的最后者

实现

template <typename T>
ListNodePosi(T) List<T>::find(T const &e, int n, ListNodePosi(T) p) const
{
    while (0 < n--)                   //对于p的最近的n个前驱，从右向左 O(n)
        if (e == (p = p->pred)->data) //逐个比对，直到命中或范围越界 假定类型T已重载==
            return p;                 //返回e的位置p
    return NULL;                      //查找失败，返回NULL
}

复杂度分析

可以类比Vector::find()，线性正比于查找区间长度，O(n)

3.3.5 插入

接口

根据不同的要求提供多种接口灵活使用

//把e当作首元素插入
template <typename T>
ListNodePosi(T) List<T>::insertAsFirst(T const &e)
{
    _size++;
    return header->insertAsSucc(e);	//e作为header的后继
}
//把e当作末元素插入
template <typename T>
ListNodePosi(T) List<T>::insertAsLast(T const &e)
{
    _size++;
    return trailer->insertAsPred(e); //e作为trailer的前驱
}
//把e当作前驱插入
template <typename T>
ListNodePosi(T) List<T>::insertBefore(ListNodePosi(T) p, T const &e)
{
    _size++;
    return p->insertAsPred(e); //e的前插入
}
//把e当作后继插入
template <typename T>
ListNodePosi(T) List<T>::insertAfter(ListNodePosi(T) p, T const &e)
{
    _size++;
    return p->insertAsSucc(e); //e的后插入
}

实现

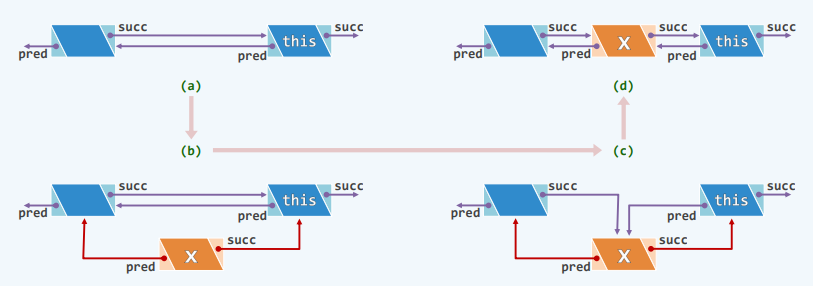
//前插入：将新元素e作为当前节点的前驱插至列表
template <typename T>
ListNodePosi(T) ListNode<T>::insertAsPred(T const &e)
{
    //创建新节点，它的前驱是当前节点的前驱，后继为当前节点
    ListNodePosi(T) x = new ListNode(e, pred, this);
    pred->succ = x; //当前节点的前驱的后继设置为x
    pred = x;       //当前节点的前驱设置为x
    return x;       //返回新节点的位置
}

//后插入：将新元素e作为当前节点的后继插至列表
template <typename T>
ListNodePosi(T) ListNode<T>::insertAsSucc(T const &e)
{
    //创建新节点：它的前驱是当前节点，后继为当前节点的后继
    ListNodePosi(T) x = new ListNode(e, this, succ);
    succ->pred = x;
    succ = x;
    return x;
}

复杂度分析

列表的插入和向量截然不同，列表的插入仅涉及局部，相当于微创手术而非牵一发而动全身，不包含任何迭代和递归，单纯的插入操作仅消耗**O(1)**常数时间。

3.3.6 基于复制的构造

列表类内部方法

首先调用init()初始化新列表，将自==p==所指节点起取出==n==个相邻节点作为末节点插入新列表

template <typename T>
void List<T>::copyNodes(ListNodePosi(T) p, int n)
{
    init();     //创建头尾哨兵节点并做初始化
    while (n--) //自p起的n项 O(n+1)
    {
        insertAsLast(p->data); //将p作为末节点插入
        p = p->succ;           //将p设置为下一项
    }
}

接口

template <typename T>
List<T>::List(ListNodePosi(T) p, int n) //复制列表中自p起的n项
{
    copyNodes(p, n);	//O(n+1)
}
template <typename T>
List<T>::List(List<T> const &L) //整体复制列表L
{
    copyNodes(L.first(), L.size());	//O(n)
}
template <typename T>
List<T>::List(List<T> const &L, int r, int n) //复制L中自第r项起的n项
{
    copyNodes(L[r], n);	//O(r+n+1)
}

显然，这种循秩访问的复制方法复杂度较高，在动态存储策略的结构中不是有效的方式。

3.3.7 删除

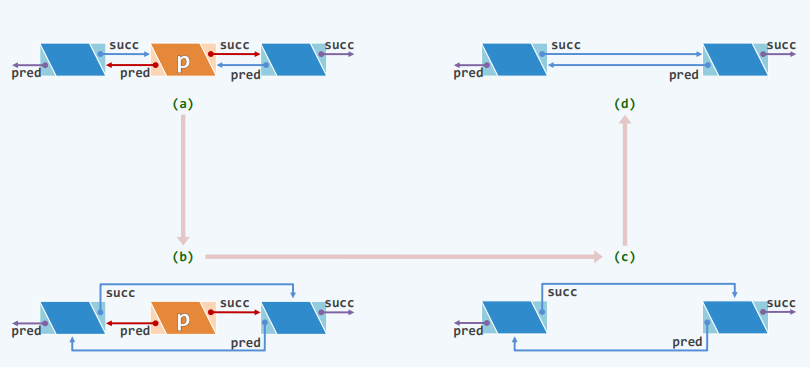
删除指定位置==p==处的节点并返回该节点的数值==e==

实现

template <typename T>
T List<T>::remove(ListNodePosi(T) p)
{
    T e = p->data;           //备份待删除节点的数值
    p->pred->succ = p->succ; //p的后继赋给p的前驱的后继
    p->succ->pred = p->pred; //p的前驱赋给p的后继的前驱
    delete p;                //释放节点
    _size--;                 //更新规模
    return e;                //返回备份数据
}

复杂度分析

和列表的插入类似的微创手术，复杂度仅为常数O(1)

3.3.8 析构

实现

template <typename T>
List<T>::~List()
{
    clear();        //清空列表
    delete header;  //释放header
    delete trailer; //释放trailer
}
template <typename T>
int List<T>::clear() //清空列表
{
    int oldSize = _size;
    while (0 < _size)	//O(n)
        remove(header->succ) //反复删除首节点直至列表变空
}

复杂度分析

除了while循环外其他操作都只需要常数时间，故整个析构方法的运行时间应该是O(n)，正比于列表原先的规模

3.3.9 唯一化

实现

template <typename T>
int List<T>::deduplicate()
{
    if (_size < 2)              //平凡情况
        return 0;               //自然没有重复
    int oldSize = _size;        //记录原规模
    ListNodePosi(T) p = header; //从首节点开始
    Rank r = 0;
    while (trailer != (p = p->succ)) //直到末节点结束	O(n)
    {
        ListNodePosi(T) q = find(p->data, r, p); //在p的r个真前驱中查找雷同者	O(r)
        q ? remove(q)                            //q存在，删除q	O(1)
          : r++;                                 //q=NULL，无重前缀的长度+1	O(1)
    }
    return oldSize - _size; //列表规模变化量，即删除元素的总数
}

正确性

分析方法和Vector<T>::deduplicate()相同，while循环的条件保证了单调性，当前查找元素的前缀一定是无重的保证了不变性。

复杂度分析

各次while循环中查找的时间是：1+2+3+...+n

根据算术级数的特点，总的复杂度为O(n²)

虽然相比于向量，删除操作的复杂度有所降低，但是渐进复杂度并没有改进。

3.3.10 遍历

实现

与向量对应的接口相仿

template <typename T>
void List<T>::traverse(void (*visit)(T &)) //利用函数指针遍历机制
{
    for (ListNodePosi(T) p = header->succ; p != trailer; p = p->succ)
        visit(p->data);
}
template <typename T>
template <typename VST>
void List<T>::traverse(VST &visit) //利用函数对象遍历机制
{
    for (ListNodePosi(T) p = header->succ; p != trailer; p = p->succ)
        visit(p->data);
}

3.4 有序列表

3.4.1 唯一化

实现

template <typename T>
int List<T>::uniquify()
{
    if (_size < 2)       //平凡情况
        return 0;        //自然无重复
    int oldSize = _size; //记录原规模
    ListNodePosi(T) p = first();
    ListNodePosi(T) q;
    while (trailer != (q = p->succ)) //反复比对紧邻的节点对(p, q)
        if (p->data != q->data)      //若互异
            p = q;                   //则转向下一对
        else                         //若雷同
            remove(q);               //删除后者
    return oldSize - _size;          //返回规模变化量，即被删除元素的总数
}

复杂度分析

思路可参考有序向量的唯一化，因为这里删除只需常数时间，所以时间成本只来自于一趟遍历，时间复杂度为O(n)

3.4.2 查找

实现

template <typename T>
ListNodePosi(T) List<T>::search(T const &e, int n, ListNodePosi(T) p) const
{
    while (0 <= n--)                    //对于p的最近的n个前驱，从右向左逐个比较
        if (((p = p->pred)->data) <= e) //若未命中
            break;                      //终止本次循环开始下一次
    return p;                           
    //直到命中，返回位置p(此时的p应为相同大小元素中位置最靠后的)
}

复杂度分析

因为动态存储策略的原因，我们无法像向量一样自如地使用减治策略，这种查找方法和无序列表的查找没有本质区别，时间复杂度依然是O(n)

3.5 排序器

3.5.1 统一入口

template <typename T>
void List<T>::sort(ListNodePosi(T) p, int n)
{
    switch (rand() % 3)
    case 1:
        insertionSort(p, n); //插入排序
    break;
case 2:
    selectionSort(p, n); //选择排序
    break;
default:
    mergeSort(p, n); //归并排序
    break;
}

3.5.3 选择排序

构思

回想BubbleSort，这种算法每趟扫描的结果是这次扫描中的最大者一定到达最终位置，完成这个目标其实只需要使这个最大者和这趟扫描的最后一个元素做交换，但是实质上BubbleSort做了O(n)次交换，我们认为这是没有必要的。

于是我们摒弃没有必要的操作，每趟扫描仅仅选出其中最大者将其置为这趟扫描的最后一个元素，可以提升效率。

稳定性

将每趟扫描的最大者置为这趟扫描的最后一个元素有两种方法

交换法
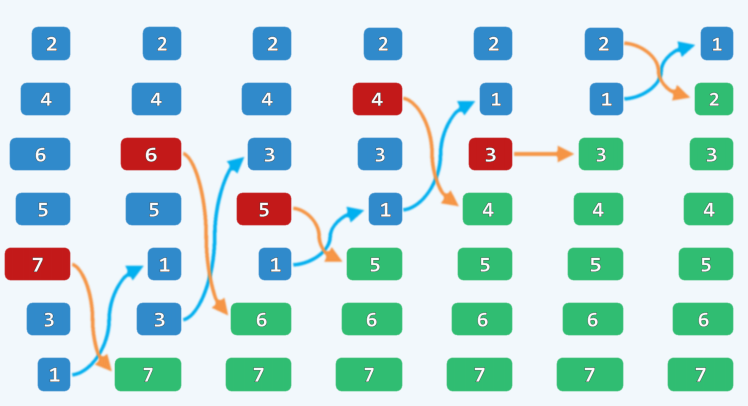
平移法

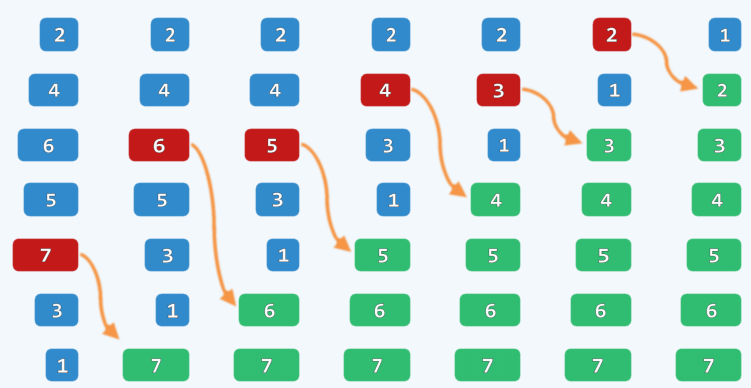
采用平移法以保证重复元素在列表中的相对次序与其插入次序是一致的。

实现

template <typename T>
void List<T>::selectionSort(ListNodePosi(T) p, int n)
{
    ListNodePosi(T) head = p->pred;
    ListNodePosi(T) tail = p;
    for (int i = 0; i < n; i++)
        tail = tail->succ; //将tail位置设置为p+n
    while (1 < n)
    {
        ListNodePosi(T) max = selectMax(head->succ, n); //在[p, n)中找最大者，重复元素则为位置靠后者
        insertBefore(tail, remove(max));                //将最大者删除的同时将最大者插入到tail前
        tail = tail->pred;
        n--;
    }
}

template <typename T>
ListNodePosi(T) List<T>::selectMax(ListNodePosi(T) p, int n)
{
    ListNodePosi(T) max = p;                  //暂定首节点为max
    for (ListNodePosi(T) cur = p; 1 < n; n--) //从首节点p出发将后续节点依次与max比较
        //!lt = not less than
        if (!lt((cur = cur->succ)->data, max->data)) //若前者不小于后者
            max = cur;                               //更新最大元素位置记录
    return max;                                      //返回最大节点位置
}

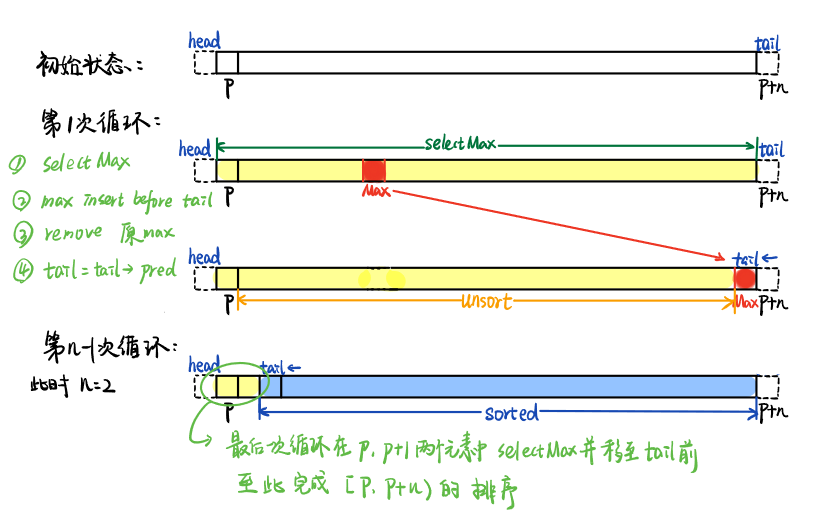
选择排序算法的不变性是在任何时刻，后缀S[r, n)已经有序，且不小于前缀S[0, r)，while循环可以保证有序后缀的规模一定会越来越大直至整体有序，这是单调性。

值得改进的地方：我们发现，调用remove()和insert()这两种操作时，会涉及动态内存分配，即new和delete，这些操作所需时间在其他基本操作的100倍左右，使用其他方式实现可以进一步提高效率。

复杂度分析

共迭代n次，在第k次迭代中

selectMax()为Θ(n - k)（呈现算术级数规律），其余操作均为O(1)，故总体复杂度应为Θ(n²)（这里没有最好最坏情况，无论怎样的无序列表，排序的复杂度都是如此）

虽然总体复杂度和BubbleSort相同，但是SelectionSort的复杂度主要源于比较（成本相对较低），而移动操作（更费时）和BubbleSort比要少很多。

3.5.2 插入排序

构思

就像摸牌一样，我们常常将摸到的牌在手中按一定的顺序排列，每摸一张新牌，就将其插入到相应的位置以保持手中的牌具有某种顺序。

这和插入排序的思想是一致的，我们可以将前一部分有序序列视为当前手里的牌，而将后面一部分尚未排序的序列视为还未摸取的牌，每次将后一部分序列的第一个元素插入到前方适当的位置，相当于摸取新的手牌的过程。

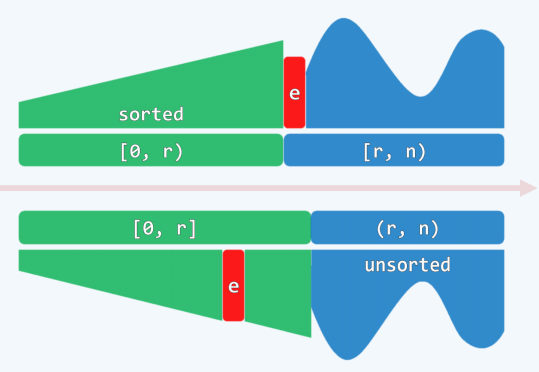
不变性：序列总能分为两部分，sorted的S[0, r) 和 unsort的U[r, n)

反复地，针对e = A[r]在S中寻找适当的位置插入。

实现

template <typename T>
void List<T>::insertionSort(ListNodePosi(T) p, int n)
{
    for (int r = 0; r < n; r++) //为各节点逐一
    {
        //在p的r个前驱中(由右至左)查找不大于p->data的位置，在该位置后插入p->data
        insertAfter(search(p->data, r, p), p->data);
        p = p->succ;     //转向下一节点
        remove(p->pred); //此时p已经指向原p的后继，删除p->pred就是删除原先完成插入的p
    }
}

复杂度分析

就地算法(in-place)：除了输入数据所占用的空间外，仅使用了O(1)的辅助空间
在线算法(online)：算法启动后待排序数据陆续到达，而不是在一开始时整体给出
具有输入敏感性(input-sensitive)：算法复杂度很大程度上取决于输入数据的特性，所以它具有最好情况和最坏情况的差距
最好情况：完全有序-每次迭代只需1次比较，0次交换：累计**O(n)**时间
最坏情况：完全逆序-第k次迭代，需O(k)次比较，1次交换：累计**O(n²)**时间

InsertionSort和SelectionSort的区别就在于此，SelectionSort无论什么情况都是Θ(n²)

利用后向分析计算平均性能

当e[r]刚完成插入的那一时刻，有序前缀[0 , r]r+1个元素中每个元素为e的概率均为1/(r + 1)，则为引入这个S[r]所花费时间的数学期望为：

[r+(r+1)+...+3+2+1+0]/(r+1)+1=r/2+1

完成整个[0, n)序列排序的总体时间的数学期望为：

\sum_{r=0}^{n-1} r / 2+1=\mathcal{O}\left(n^{2}\right)

从逆序对的角度考虑

规定：如果两个元素构成逆序对，那么将逆序数计入靠后的元素

当我们要将一个来自无序后缀的元素e插入到有序前缀时，

在有序前缀中，插入位置前方元素均小于等于e，而插入位置后方元素均大于e，后方元素的数量即在原位置时的e的逆序数i(e)，则i(e)就是e在插入过程中需要比较的次数，则完成总体排序需要的比较次数就是这个序列所有元素的逆序数之和I

除此之外，在循环过程中（平均）发生交换的次数为n，每次交换所需时间为O(1)，故完成总体排序中交换需要O(n)的时间

比较和交换所需时间相加就是完整总体排序所需时间总和，O(I + n)，最好情况下没有逆序对，I = 0，时间复杂度为O(n)；最坏情况下每对元素都构成逆序对，逆序数为C²_n 即O(n²)，印证了前面的分析。

3.5.4 归并排序

实现

template <typename T> //有序列表的归并：当前列表中自p起的n个元素，与列表L中自q起的m个元素归并
void List<T>::merge(ListNodePosi(T) & p, int n, List<T> &L, ListNodePosi(T) q, int m)
{
    // assert: this.valid(p) && rank(p) + n <= size && this.sorted(p, n)
    // L.valid(q) && rank(q) + m <= L._size && L.sorted(q, m)
    // 注意：在归并排序之类的场合，有可能 this == L && rank(p) + n = rank(q)
    ListNodePosi(T) pp = p->pred;            //借助前驱（可能是header），以便返回前 ...
    while (0 < m)                            //在q尚未移出区间之前
        if ((0 < n) && (p->data <= q->data)) //若p仍在区间内且v(p) <= v(q)，则
        {
            if (q == (p = p->succ))
                break;
            n--;
        }    //将p替换为其直接后继（等效于将p归入合并的列表）
        else //若p已超出右界或v(q) < v(p)，则
        {
            insertBefore(p, L.remove((q = q->succ)->pred));
            m--;
        }         //将q转移至p之前
    p = pp->succ; //确定归并后区间的（新）起点
}

template <typename T> //列表癿弻幵排序算法：对起始亍位置p癿n个元素排序
void List<T>::mergeSort(ListNodePosi(T) & p, int n)
{ //valid(p) && rank(p) + n <= size
    if (n < 2)
        return;     //若待排序范围已足够小，则直接返回；否则...
    int m = n >> 1; //以中点为界
    ListNodePosi(T) q = p;
    for (int i = 0; i < m; i++)	  //O(n)
        q = q->succ; //均分列表
    mergeSort(p, m);
    mergeSort(q, n - m);          //对前、后子列表分别排序
    merge(p, m, *this, q, n - m); //归并
} //注意：排序后，p依然指向归并后区间的（新）起点

复杂度分析

对长度为n的列表做归并排序，花费O(n)的时间确定居中的切分节点，然后递归地对长度均为n/2的两个子列表做归并排序，最后花费线性时间做二路并归，其复杂度应为O(nlogn)