1.导论
边缘检测
视觉分层 :第一层是边缘结构
识别问题:图像分类(旧时用特征->svm)
超参数:由验证集确定,若训练集较小,交叉验证(例如10折,训练集分成10份,某超参x下取9份训练10次,求剩下一份验证集的平均值,作为该超参的效果,再进行比较,但消耗资源)
2.分类器
2.1 最近邻分类器knn
对测试集中的图片,找训练集中最相近的几张图片,进而判断标签
2.2 线性分类器
- 讲解一个线性映射
- 多类svm折页损失函数
- 正则化惩罚
增加权重W的一些偏好,常采用L2范式,因为为了拟合一些异常点时,较大的w才会产生较大的导数,W<1时,惩罚项越来越小 - softmax分类器
3.神经网络
理解网络特征:
3.1 损失函数
- 为什么用交叉熵做损失函数
信息量(自信息):首先寻找一个函数,满足:(1)是p(x)的单调函数(2)两个不相关事件x,y,同时观察他们获得的信息量==单独观察之和:I(x,y)=I(x)+I(y),且p(x,y)=p(x)p(y),因此得到对数函数I(x)=-log(p(x)),负号保证正数和某个事件的发生带来的信息量与概率相反
信息熵:消除不确定性所需信息量的度量,信息越确定,信息熵越小,反之越需要更多信息来确定=>对信息量的期望
相对熵(KL散度):对于同一个随机变量xx有两个单独的概率分布p(x)和p(y),可以使用相对熵来衡量这两个分布的差异。
交叉熵: 由于相对熵=交叉熵-信息熵,由于信息熵固定,优化交叉熵即可
3.2 激活函数
- 为什么要激活函数:输入输出间复杂的非线性映射,逼近复杂函数映射(联想线条弯曲的图)
Sigmoid:梯度消失,输出不是以0为中心
Tanh:梯度消失,输出以0为中心
ReLU:分段线性,总体不是线性,可以拟合任何,优点:(1)前两者耗费计算资源,这个只用阈值或者矩阵或者if else(2)收敛加速快(3)梯度消失问题(4)稀疏性。缺点:(1)不是0均值(2)不会对数据做幅度压缩,数据幅度会扩张(3)神经元坏死现象:参数永远不会被更新:两个原因:参数初始化/学习率太高使训练过程中参数更新太大
Leaky relu:解决死亡问题。
3.3 数据预处理
1. 零中心化;
2.减去均值/归一化:再除以标准差来调制数值范围(得到均值为0,方差为1的正态分布,使不同维度具有同样的范围),因为每个样本由多个特征,然而特征的量纲和量级不一样,这样就具有相同尺度
3.PCA和白化:比如从ND降到N100,留下最大方差的100个维度(但卷积网络中不会采用)
,然后再执行方法。执行完后线程释放对象,执行过程中其他线程无法获取到Monitor对象。
3.4 权重初始化
BN层可以减少权重初始化的依赖
1.不能全零等相同值,因为输出值相同、反向传播中相同、从而同样的参数更新,不再对称性
2.小数随机初始化,W=0.01*np.random.randn(D,H),但小数值不一定好,反向时梯度太小
3.使用1/sqrt(n)校准方差
//**参考:**www.cnblogs.com/shine-lee/p…
**预备知识:**E(w)=0;需要对var(w)控制;不同激活层输入的方差相同;应考虑前后两个过程
期望与方差:

计算过程


因为a,z输入输出希望同分布,所以w的方差为i/fan_in,np.random.randn(n)/sqrt(n),因为随着数据量增大,数据分布x的方差也在增大,可以除以数据量的平方根来调整范围,这样保证神经元起始时有近似同样的输出分布,是归一化的。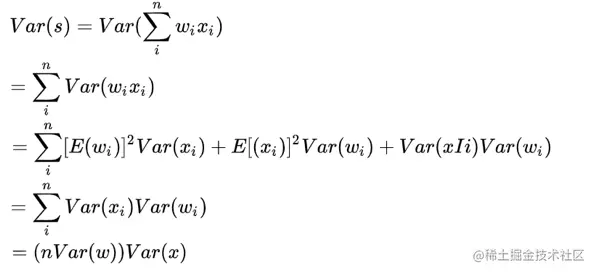
Understanding the difficulty of training deep feedforward neural networks中有类似的分析。在这篇论文中,作者的结论是建议初始化的形式是Var(w)=2(nin+nout),其中nin,nout分别是上一层和下一层神经元的数量。Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification推导了ReLU神经元的权重初始化问题,得出的结论是神经元的方差需要是2.0/n,即w=np.random.randn(n)/sqrt(2.0/n),这是目前在神经网络中使用相关神经网络的建议。
4.稀疏初始化
5.偏置初始化
3.5 正则化
1.**L1\L2正则化,组合 **
2.最大范式约束,给权重设置上限,这样也不会爆炸
3.6 参数更新
1.一阶方法:随机梯度下降、动量
2.学习率退火:学习率衰减:随步数衰减、指数衰减、1/t衰减
3.二阶:牛顿法
4.逐参数适应学习率方法:Adagrad/RMSprop/Adam
补:参数计算:卷积和个数宽高*厚度
3.7 批归一化
原因:
1.在输入层上,一部分样本与另一部分显著不同,[0,1]与[10,100],那么对浅层模型而言,一会描绘模型a,一会b,推翻自己的劳动,没有效率。同理,在其余层中,前一层的输出也会带来这种情况,所以需要均值=0方差=1;同时可以对梯度消失有用。
2.第四步理解为:对sigmoid来说,限制在正态分布的区域非线性表达能力会下降,且让每一层自己学习是否需要平移和缩放来切合原始数据的分布
前面3步就是归一化的过程,得到正态分布的,可sigmoid在[-1,1]间梯度变化不大,非线性弱,并且数据本身不对称,正态分布不是最理想的,那第四步就是为了避免限制在正态分布带来的网络表达能力下降的问题:尺度变换和偏移,缩放了方差和改变了均值,使新分布切合真实分布=>测试时的bn来源于训练时的保留下来的整个样本的均值和方差,作为测试样本的均值和方差
此外,BN的作用也是控制每层输入(下一层的输入)的模值,稍微解决点梯度的爆炸/消失现象。
为什么梯度消失或者爆炸,举例如下,反向传播结果的数值大小不止取决于求导的式子,很大程度上也取决于输入的模值,当计算图每次输入的模值都大于1,那么经过很多层回传,梯度将不可避免地呈几何倍数增长。BN的作用本质上也是控制每层输入的模值,因此梯度的爆炸/消失现象理应在很早就被解决了(至少解决了大半)。
3.8 防止过拟合
1.数据增强:图像变换和水平翻转、改变RGB通道强度
2.dropout
3.正则化