在可视化应用中,我们经常会遇到需要判断一个路径是否存在交叉的需求。根据路径交叉与否可以判断多边形是否是简单多边形,以及判断交通路线是否有十字路口等等。

不交叉的路径(左)与交叉的路径(右)
这个问题实际上本质上是判断两个线段是否相交。因为路径是由线段构成,我们只要判断除了相邻线段外,没有其他线段两两相交即可,JS代码如下:
function isPathIntersection(points) {
const len = points.length;
for(let i = 0; i < len - 1; i++) {
const point = points[i];
const nextPoint = points[i + 1];
for(let j = 0; j < len - 1; j++) {
const p1 = points[j],
p2 = points[j + 1];
if(p1 !== point && p2 !== point && p1 !== nextPoint && p2 !== nextPoint
&& isCross(p1, p2, point, nextPoint) && isCross(point, nextPoint, p1, p2)) {
return true;
}
}
}
return false;
}
上面的代码,实际上就是用两个循环遍历路径中的每条线段,判断两两线段是否相交,判断逻辑实现在isCross函数中。
那么isCross函数该怎么实现呢?我们来分析一下。
如下图所示,向量(p3, p4)与向量(p1, p2)所在的直线相交,那么向量(p1, p3)(记为A)和向量(p3, p2)(记为B)就在向量(p3, p4)(记为C)的两侧,那么就应该满足 C X B 和 C X A 的符号相反,也就是左侧这个图。反之,如果向量(p3, p4)与向量(p1, p2)所在直线不相交,那么向量(p1, p3)(记为A)和向量(p3, p2)(记为B)就在向量(p3, p4)(记为C)的同一侧,也就是 C X B 和 C X A 的符号相同。
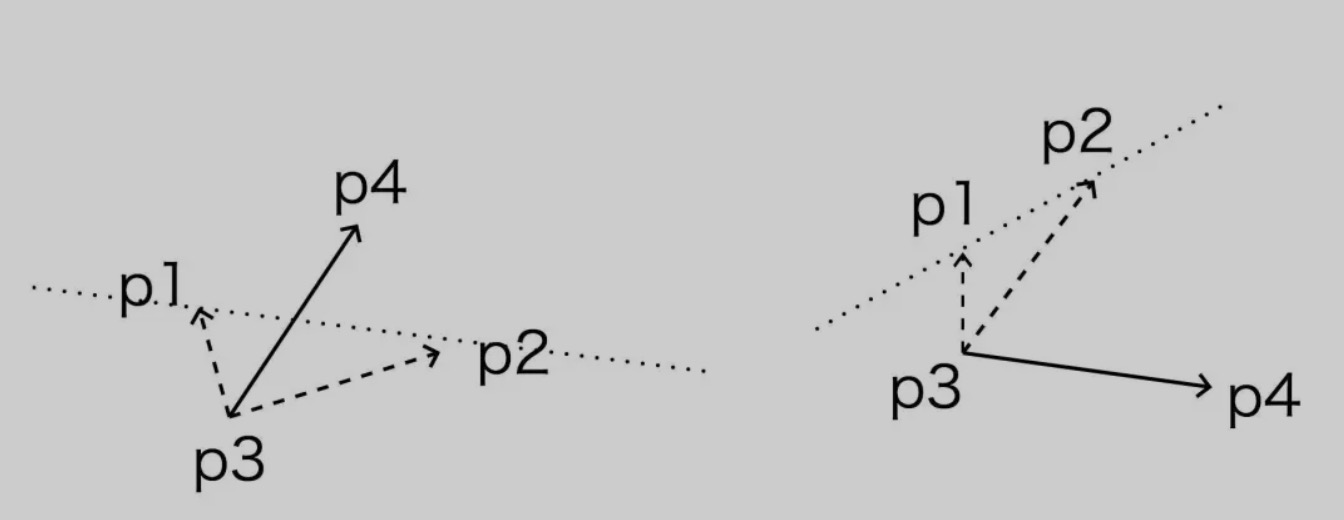
所以呢,我们根据这个原理,就可以实现 isCross 函数,如下:
function isCross(p1, p2, p3, p4) {
const v1 = subtract([], p4, p3);
const v2 = subtract([], p1, p3);
const v3 = subtract([], p2, p3);
const z1 = cross(v1, v2);
const z2 = cross(v1, v3);
return z1 * z2 <= 0;
}
其中subtract是向量减法,cross是向量叉积。
那么为什么在 isPathIntersection 中,isCross 要判断两次?
isCross(p1, p2, point, nextPoint) && isCross(point, nextPoint, p1, p2)
这是因为,线段A(p1, p2)和B(p3, p4)相交必须同时满足A在B所在直线的两侧和B在A所在直线的两侧。
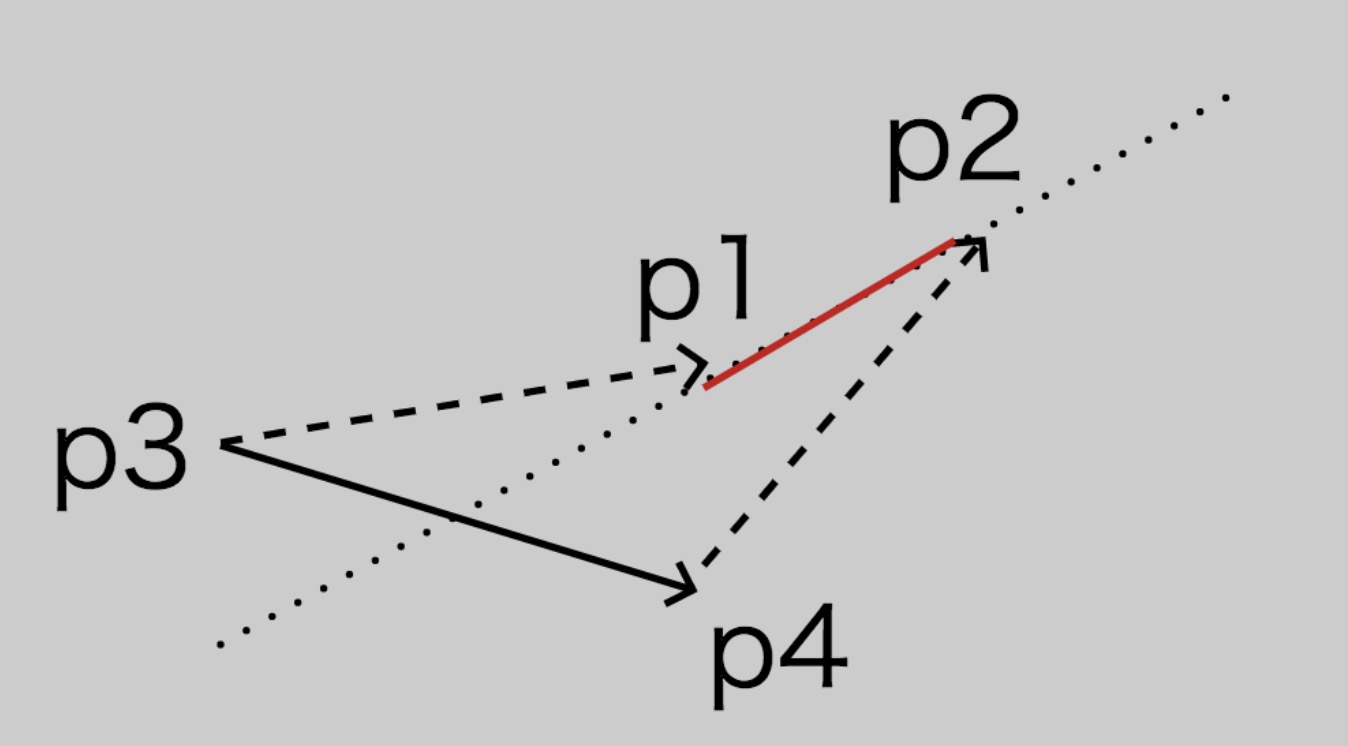
比如上面这个图的情况,就是 isCross(p1, p2, p3, p4) 是 true,但是 isCross(p3, p4, p1, p2) 却是 false,两个线段并不相交。
所以,这样我们就实现了全部功能,完整代码并不复杂,如下:
import {subtract, cross} from '../common/lib/math/functions/Vec2Func.js';
function isCross(p1, p2, p3, p4) {
const v1 = subtract([], p4, p3);
const v2 = subtract([], p1, p3);
const v3 = subtract([], p2, p3);
const z1 = cross(v1, v2);
const z2 = cross(v1, v3);
return z1 * z2 <= 0;
}
function isPathIntersection(points) {
const len = points.length;
for(let i = 0; i < len - 1; i++) {
const point = points[i];
const nextPoint = points[i + 1];
for(let j = 0; j < len - 1; j++) {
const p1 = points[j],
p2 = points[j + 1];
if(p1 !== point && p2 !== point && p1 !== nextPoint && p2 !== nextPoint
&& isCross(p1, p2, point, nextPoint) && isCross(point, nextPoint, p1, p2)) {
return true;
}
}
}
return false;
}
function draw(context, points) {
context.clearRect(0, 0, context.canvas.width, context.canvas.height);
const d = `M${points.join('L')}`;
const color = isPathIntersection(points) ? 'red' : 'blue';
context.strokeStyle = color;
const path = new Path2D(d);
context.stroke(path);
}
const canvas = document.querySelector('canvas');
const ctx = canvas.getContext('2d');
ctx.lineWidth = 5;
ctx.lineJoin = 'round';
ctx.lineCap = 'round';
const points = [];
canvas.addEventListener('click', (evt) => {
const {x, y} = evt;
const {x: x0, y: y0} = evt.target.getBoundingClientRect();
points.push([x - x0, y - y0]);
draw(ctx, points);
});
canvas.addEventListener('dblclick', (evt) => {
points.length = 0;
draw(ctx, points);
});
最终的效果如下:
