author:cris
1. 使用稀疏数组优化二维数组
1.1 应用场景
我们小时候应该都玩过五子棋
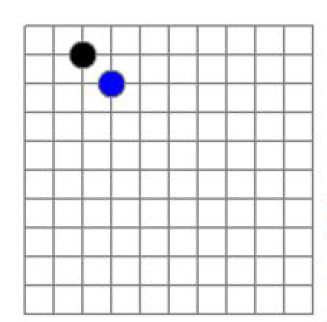
而对于上面的五子棋,如果我们想要存储此时的棋盘状态(第二行第三列有个黑子,第三行第四列有个蓝子),可以使用二维数组来保存,例如此棋盘是
11 * 11 的布局,那么我们可以使用如下的二维数组来保存(其中1表示黑子,2表示蓝子)

先初始化一个二维数组
int[][] array = new int[11][11];
然后将对应棋子的位置信息存储即可,比如对于第二行第三列有个黑子表示如下
array[1][2]
此时如果我们想要保存该游戏状态到磁盘上,方便下次读取直接恢复(存盘退出以及恢复上盘),就可以将当前的二维数组保存到磁盘上。但我们发现,其实这个二维数组有很多元素都是0 这些没有存储价值的数据,此时我们就可以使用 稀疏数组 来进行数据的优化存储。
1.2 稀疏数组的基本介绍
当一个数组中大部分元素为0,或者为同一个值的数组时,可以使用稀疏数组(也是二维数组)来保存该数组。
稀疏数组的处理方法是:
- 记录数组一共有几行几列,有多少个不同的值
- 把具有不同值的元素的行列及值记录在一个小规模的二维数组中,从而缩小程序的规模
例如以上的棋盘映射的二维数组,如果转换成稀疏数组,那么结构如下
| 行(row) | 列(col) | 值(val) |
|---|---|---|
| 11 | 11 | 2 |
| 1 | 2 | 1 |
| 2 | 3 | 2 |
其中这个稀疏数组的第一行默认为记录原始二维数组信息(原始数组有多少行,多少列,几个值,方便稀疏数组向原始二维数组的转换);接下来的每一行就是记录原始数组中的每个棋子的行和列信息,以及值信息(1表示黑子,2表示蓝子),这样子就可以大大降低存储空间。
1.3 代码思路
-
二维数组装换成稀疏数组
- 遍历原始的二维数组,得到有效值的个数 sum
- 根据有效值的个数,就可以创建稀疏数组 int[] [] sparseArr = new int [sum+1] [3]
- 将二维数组的有效值存入到稀疏数组即可
-
稀疏数组转换成原始二维数组的思路
- 先读取稀疏数组的第一行,用于创建原始数组的结构
- 再读取稀疏数组的有效数据的行,列,值 信息,赋值给原始数组即可
1.4 示例代码
public class SparseArray {
public static void main(String[] args) {
// 初始化原始数组
int[][] array = new int[11][11];
// 黑子和蓝子的位置信息初始化
array[1][2] = 1;
array[2][3] = 2;
// 记录原始数组有多少个有效值
int sum = 0;
for (int[] ints : array) {
for (int anInt : ints) {
if (anInt != 0) {
sum++;
}
}
}
// 初始化稀疏数组(列数固定为3,行数=有效值个数+1)
int[][] sparseArray = new int[sum + 1][3];
// 稀疏数组的第一行值是固定的(原始数组的行数,列数,有效值的个数)
sparseArray[0][0] = 11;
sparseArray[0][1] = 11;
sparseArray[0][2] = sum;
// 引入一个计数器,用于记录当原始数组有一个有效值就+1,并且进行稀疏数组的复制(每个原始数组的有效值的行数,列数,值
// 都最终保存在稀疏数组的一行中)
int count = 0;
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
if (array[i][j] != 0) {
count++;
sparseArray[count][0] = i;
sparseArray[count][1] = j;
sparseArray[count][2] = array[i][j];
}
}
}
// 遍历原始数组
for (int[] ints : array) {
for (int anInt : ints) {
System.out.printf("%d\t", anInt);
}
System.out.println();
}
System.out.println("-----------------------------------------------");
// 遍历稀疏数组
for (int[] ints : sparseArray) {
for (int anInt : ints) {
System.out.printf("%d\t", anInt);
}
System.out.println();
}
// 初始化新的二维数组
int[][] array2 = new int[sparseArray[0][0]][sparseArray[0][1]];
// 给二维数组赋有效值
for (int i = 1; i < sparseArray.length; i++) {
array2[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2];
}
System.out.println("-----------------------------------------------");
// 遍历新的二维数组
for (int[] ints : array2) {
for (int anInt : ints) {
System.out.printf("%d\t", anInt);
}
System.out.println();
}
}
}
1.5 拓展(数据的保存和读取)
如果要将稀疏数组存入到磁盘中,然后需要使用的时候再从磁盘读取,我们可以使用Java 的IO 以及序列化来操作
// 将稀疏数组序列化写入到磁盘中
try {
FileOutputStream fileOutputStream = new FileOutputStream("./data.ser");
ObjectOutputStream objectOutputStream = new ObjectOutputStream(fileOutputStream);
objectOutputStream.writeObject(sparseArray);
} catch (IOException e) {
e.printStackTrace();
}
try {
// 从磁盘中读取序列化后的稀疏数组数据(反序列化)
FileInputStream fileInputStream = new FileInputStream("./data.ser");
ObjectInputStream objectInputStream = new ObjectInputStream(fileInputStream);
sparseArray = (int[][]) objectInputStream.readObject();
} catch (IOException | ClassNotFoundException e) {
e.printStackTrace();
}
2. 数组模拟环形队列
2.1 应用场景和介绍
当我们去银行排队的时候,先排队的人先被服务,这就是“先进先出”的概念,反映到程序中,就是一个队列的数据结构,如下
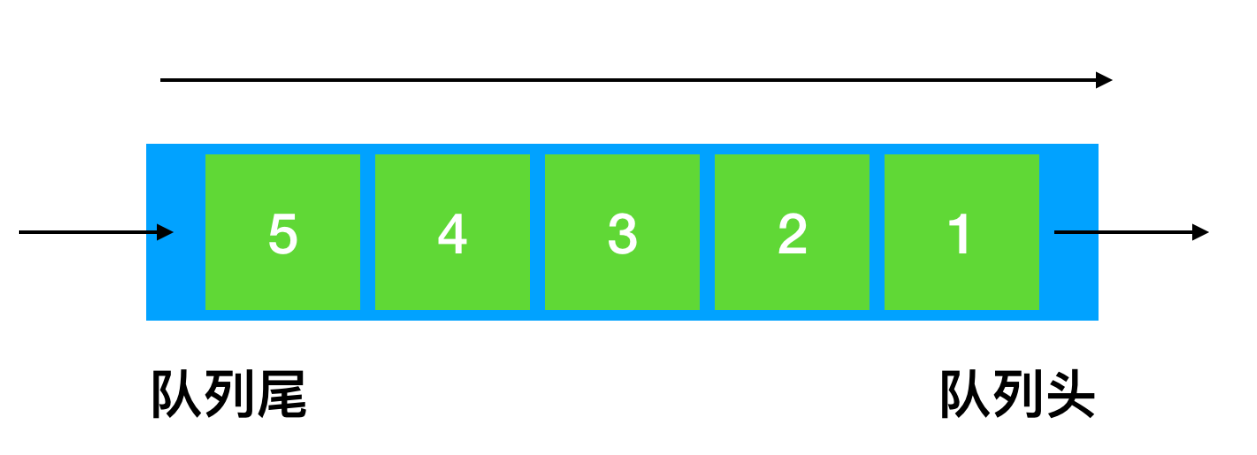
相当于队列数据结构有两个口子,一个进,一个出,先进去的元素,就先被取出,但是这样子的队列问题是,当我们把队列尾巴填充满以后,就无法继续添加元素了,即使队列头的元素被取出来有了空位置。所以我们经常使用的其实是环形队列的结构
而一个环形的队列,就是当队列装满的时候,队列头的数据被取出时,我们又可以继续添加数据到队列头,相当于队列的头和尾巴连接起来,形成了一个环形,是一个看起来封闭的数据结构
结构如下:
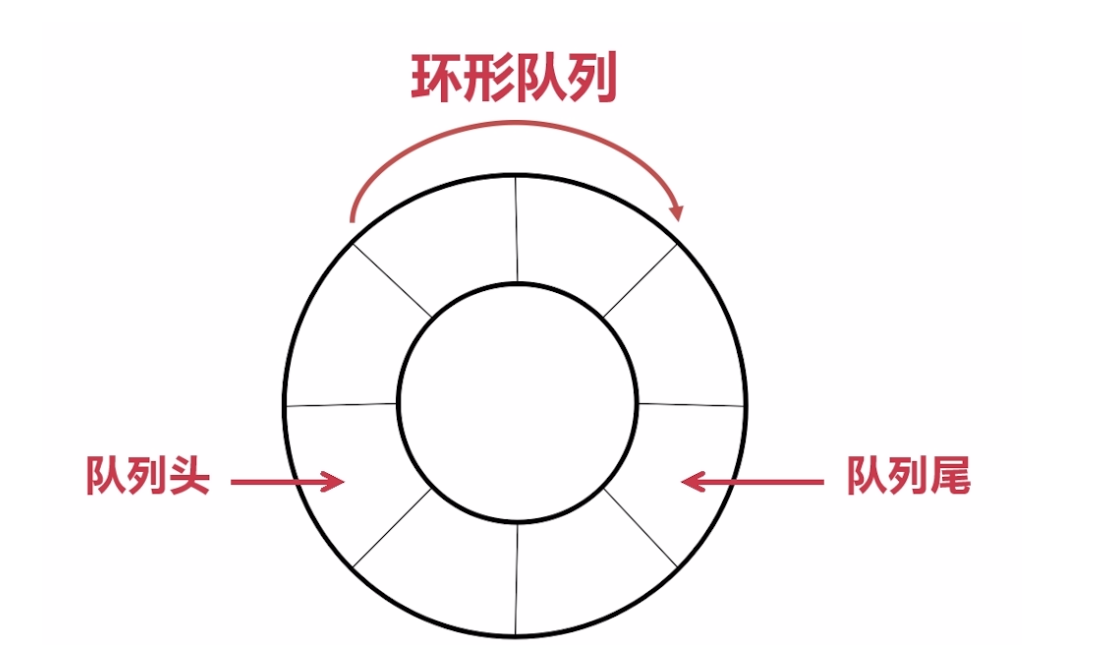
如果我们使用数组来模拟上述的环形队列数据结构,那么图解如下
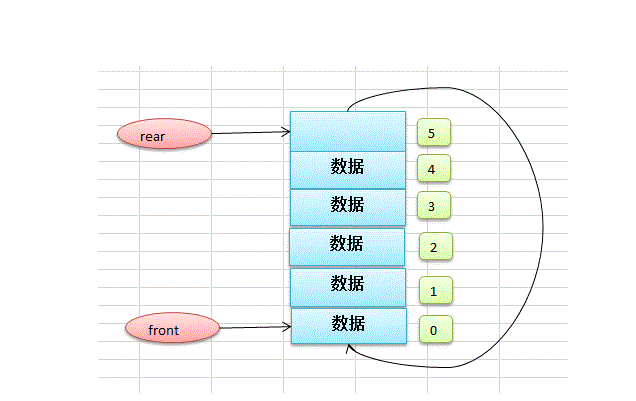
我们会定义一个数组,然后再定义两个int 类型的指针,其中 front 指针始终表示头元素的索引,而rear 指针始终表示尾元素的下一个索引位置
这样导致的一个问题就是,我们的数组始终有一个位置是空的,无法填充数据,且这个位置永远被 rear 指向
2.2 代码思路
先定义一个类数组队列,然后成员变量有一个数组 array,两个索引 front 和 rear,一个 maxSize 用于表示最大可存储的数量(值就是 array.length),但是实际存储元素个数最多为 maxSize -1,然后具体的方法思路如下:
-
判断数组队列是否为空
当 front == rear 的时候,头元素的索引和尾元素的索引相等,数据队列为空,可以存储数据,但是无法取出数据
-
判断数组队列是否满了
当 (rear + 1) % maxSize == front 的时候,数组队列无法再填充数据,此时数组队列实际存储了 (array.length - 1 个元素 + 一个空元素)
-
向数组队列添加元素
判断数组队列是否满了,如果没有满,那么添加元素到队列尾部,然后 rear = (rear+1) % maxSize,注意 rear 不能只 ++,否则会出现索引越界异常
-
从数组队列取出元素
判断数组队列是否是空的,如果有元素,那么取出 front 指向的头元素,并且 front = (front + 1) % maxSize,原因同上
-
判断数组队列的有效元素个数
size = (rear + maxSize - front)% maxSize,这里不能简写成 (rear - front)% maxSize,因为 size 必须 >= 0
-
遍历数组队列的所有有效元素
循环从 front 开始,遍历 size 次即可(因为有 size 个有效元素),每次取出的元素的索引为当前的 i 去 % maxSize
-
查看数组队列的头元素
队列为空,则没有头元素,否则返回 front 索引位置的元素即可
2.3 示例代码
public class CircleArrayQueue_02 {
public static void main(String[] args) {
// 因为始终rear 指向的是末尾元素的下一个位置(所以有一个位置始终是空的,我们如果想要初始化存储x个元素的数组队列,就要传入x+1)
CircleArrayQueue arrayQueue = new CircleArrayQueue(4); // 数组队列实际能存储3个元素
Scanner scanner = new Scanner(System.in);
char c = ' ';
boolean flag = true;
while (flag) {
System.out.print("s(显示队列) " + "a(添加元素到队列) " + "r(取出队列元素) " + "p(查看队列头元素) " +
"e(队列是否为空) " + "f(队列是否已满) " + "输入n退出");
System.out.println();
char input = scanner.next().charAt(0);
switch (input) {
case 's':
arrayQueue.showAllElement();
break;
case 'a':
System.out.println("请输入元素:");
arrayQueue.addElement(scanner.nextInt());
break;
case 'r':
System.out.println(arrayQueue.getElement());
break;
case 'p':
System.out.println(arrayQueue.headElement());
break;
case 'e':
System.out.println(arrayQueue.isEmpty());
break;
case 'f':
System.out.println(arrayQueue.isFull());
break;
case 'n':
flag = false;
}
}
}
}
class CircleArrayQueue {
private int[] array;
// 数组队列可以填充元素的最大次数,就是 array 的length
private int maxSize;
// 指向数组队列的首位元素,初始值为0
private int front;
// 指向数组队列的末尾元素的下一位空的位置,初始值为0
private int rear;
public CircleArrayQueue() {
}
// 初始化一个长度为length 的数组队列
public CircleArrayQueue(int length) {
if (length <= 0) {
throw new RuntimeException("初始化失败,the length is" + length);
}
this.array = new int[length];
maxSize = length;
}
public boolean isFull() {
return (rear + 1) % maxSize == front;
}
public boolean isEmpty() {
return rear == front;
}
// 添加数据到队列
public boolean addElement(int element) {
if (isFull()) {
System.out.println("队列已经满了,添加元素失败");
return false;
}
array[rear] = element;
// 修改rear 的值(因为是模拟的是环形队列,所以rear的值最大是maxSize - 1 )
rear = (rear + 1) % maxSize;
return true;
}
// 取出队列的数据
public int getElement() {
if (isEmpty()) {
throw new RuntimeException("队列为空,无法取出数据");
}
int temp = array[front];
// 修改front 的值(因为是模拟的是环形队列,所以front的值最大是maxSize - 1 )
front = (front + 1) % maxSize;
return temp;
}
// 显示队列所有数据
public void showAllElement() {
if (isEmpty()) {
System.out.println("队列为空,没有数据可以显示");
return;
}
// 从 front 开始遍历
for (int i = front; i < front + size(); i++) {
System.out.printf("array[%d]=%d\t", i % maxSize, array[i % maxSize]);
}
System.out.println();
}
// 求出当前数组队列的有效数据的个数
public int size() {
return (rear + maxSize - front) % maxSize;
}
// 显示队列的头数据(但是不取出)
public int headElement() {
if (isEmpty()) {
throw new RuntimeException("队列为空,没有数据可以显示");
}
return array[front];
}
}
2.4 总结
- front 和 rear 指针分别表示的含义一定要清楚(front 表示头元素的位置,rear 表示尾元素的下一个空元素的位置)
- 通过数组模拟环形队列,本质上就是利用 front,rear 和 maxSize 的相互 %