透视投影变换矩阵推理:
- 先将透视投影变成正交投影的形式
同理:
2、所以,x、y、z的变化可以写成以下形式,再都乘以一个固定的z,还是表示同一个点
3、现在我们要算出左边这个4x4的变换矩阵
根据数据,我们可以补填出的部分数字:
4、通过两个已知条件
1)任何一个点在近平面上不会发生任何变化
2)远平面上的点的z不会变化
可以求出剩下的数字
5、根据条件一
此时矩阵的未知的第三行和近平面上的点相乘等于n平方,由此可以推断出前两个数为0
所以:
6、根据条件二
取一个特殊的点,即远平面的中心点,它的位置也没有发生变化
7、将上面两个式子联立,可以解出
8、将上面的矩阵和正交投影矩阵结合,就可以得出最终的透视投影矩阵
思考:虽然远近平面上的点的z在透视变为正交时没有变,那中间的点的z是如何变化的?是推向近平面还是推向远平面?
答:视锥体内的点被挤压的更偏向了远平面f
知乎上这位 小猫耳朵 同学写得很详细,在此引用以下:
zhuanlan.zhihu.com/p/122411512
以下是摘取的主要证明内容:
透视变为正交时,f(z) = z′/w′ = n+f-nf/z,当0<n<z<f时,n+f-nf/z跟z的大小关系:
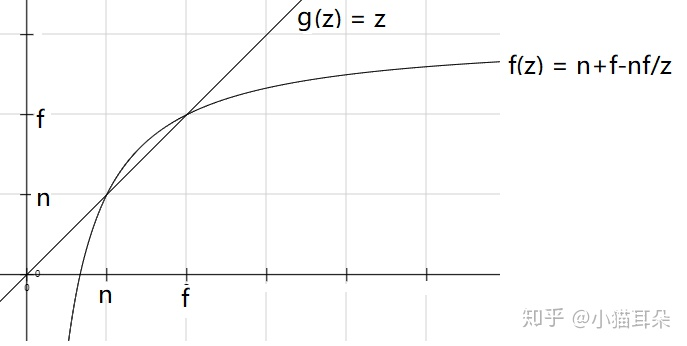
在n-f这段区域中,f(z)是大于g(z)的,所以视锥体内的点被挤压的更偏向了远平面f