typescript的类型编程是什么?
大家在平时写typescript的代码时,用到的最多功能应该是它的类型标注,给变量加上类型约束,一方面是方便自己的编码,避免明显的bug,另外一方面是增强了代码的可读性。因为js语言的灵活性比较高,typescript的类型系统也被设计得比较强大,甚至强大到可以单独作为一门编程语言。下面的内容就是论证了typescript的类型系统确实可以作为一门编程语言,并用typescript的类型系统实现了四则运算。
为什么要介绍typescript的类型元编程?
typescirpt的类型元编程属于奇技淫巧,在日常工作中很难会用到,没什么卵用。但是了解这方面可以帮助扩展视野,加深对typescript类型系统的理解,此外也能够让我们了解到编程语言的本质。
一. 图灵完备
为了讲解图灵完备,需要介绍一下图灵机的概念,但是为了降低门槛,这里先来讲解最简单的计算模型:有限状态自动机。
有限状态自动机
有限自动机可以理解为一个理论上的机器,它由一个有限的内部状态集和一组控制规则组成。在给定输入字符串的情况下,它会根据事先制定好的控制规则来自动运行(这就是自动机的由来嘛),具体来讲,自动机在每步运行时,会按照字符串的顺序读入一个字符,然后根据当前读入的字符和当前的状态,来决定转向哪个状态,至于具体转向哪个状态则由控制规则来确定。
下面的图解能够大概描述自动机的运行过程
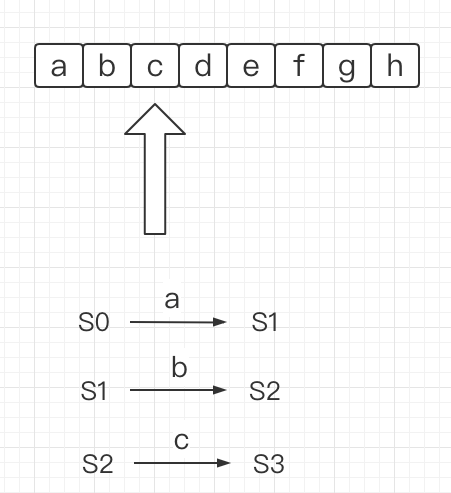
其中,箭头指向当前输入的字符,刚开始自动机的初始状态是S0,在读入第一个字符后,内部状态从S0变成S1,在读入第二个字符b后,状态从S1变为S2,之后的过程以此类推,直到自动机读完所有的输入字符。
有限状态自动机的作用
在了解有限自动机的原理后,不免会有一个疑问,这种东西到底有什么用? 实际上,有限自动机与正则表达式是等价的。一个正则表达式可以转换成一个有限自动机,反之亦然。
比如说,现在有个正则表达式:a(b|c)*d,我们可以把它转化成如下的自动机:
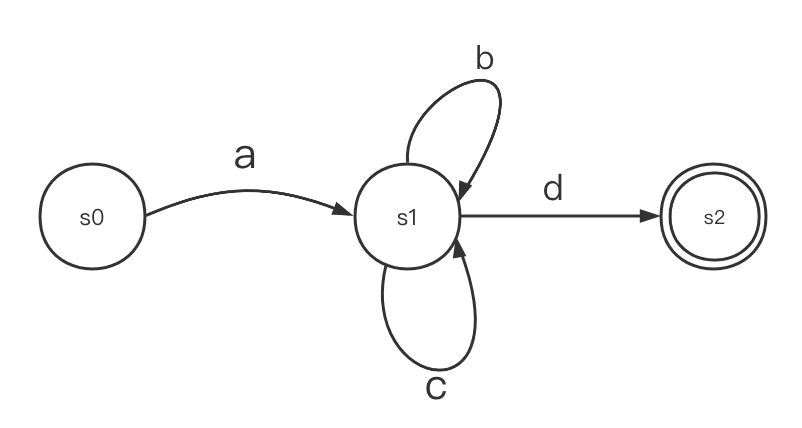
这个自动机有三个状态,其中s0是初始状态,s2是接受状态。刚开始时,自动机处在s0状态,当读入字符a时,状态就变为s1,之后,无论读入多少字符a和b,状态仍为s1,此时一旦读入字符d时,状态就变为s2(接受状态)。 而如果自动机的最终状态停留在s2时,就表明输入字符串能够被该自动机所接受,也就是说该字符串能够被该正则表达式所描述。实际上,正则表达式的内部实现原理就是用自动机来实现的。
有限自动机的扩展 —— 图灵机
虽然有限自动机很有用,可以用于匹配正则表达式,但是它的计算能力是有局限性的。比如说现在有一个字符串类似于000...111,字符串的前半部分全是0,后半部分全是1,问0的个数和1的个数相等吗?仔细想一想,像这类字符串能不能用正则表达式来描述?
答案是不能的,既然不能用正则表达式来描述,自然也就不能被有限自动机计算。至于为什么不能,这里就不再展开了,不过可以简单地提一下,正则表达式与正则文法是等价的,而上述字符串是不能用正则文法来描述的,至少要用上下文无法文法才能描述,所以有限自动机无法判定在给定的字符串中0和1的个数是否相等。
既然有限自动机的计算能力是有限的,那能否扩展一下这个自动机,从而让它的计算能力更加强大?
答案是当然可以。
接下来我们就扩展一下这个自动机让它变成图灵机。
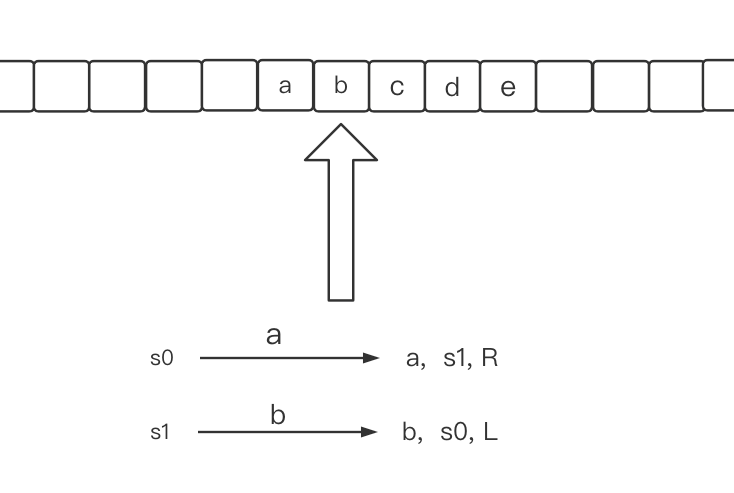
首先图灵机会有一个无限长的纸带,纸带上的一个格子可以储存一个字符,图灵机的指针不仅可以右移还可以左移,此外,图灵机还可以擦写当前的字符。和图灵机相比,有限自动机则有太多局限性了,有限自动机没有纸带,只能挨个挨个地读入输入字符串,指针只能右移不能左移,也不能修改当前字符,唯一所能做的操作是改变自身状态,而图灵机在读入一个字符后,可以做出三种操作:擦写当前字符,修改自身状态和决定指针左移还是右移。
例如在上面的图例中,图灵机的输入字符串是abcde,放在纸带中间,两边则是无限延伸的空白纸带。这个图灵机有两个状态s0,s1,刚开始时,初始状态是s0,在读入字符a后,做出三种操作:擦写当前字符为a(也就是没有改变当前字符),状态变为s1,指针右移;接着,在读入当前字符b后,又做出三种操作:擦写当前字符为b(同样地,当前字符并没有改变),状态变为s1,指针左移。
最后发现了没有?其实这个图灵机会不停地在字符a和b之间来回切换,永不停止。所以图灵机和有限自动机还有一个区别:有限自动机在读完字符串后肯定会停止,而图灵机有可能永不停机,即陷入无限循环当中。
有限自动机在被扩展后变为图灵机,那它的计算能力会有多大的提高呢?事实上,图灵机的计算能力非常强大,任何一个可以被描述的算法都能被图灵机所实现,是目前已知最强大的计算模型,你没有办法找出比它更强大的计算模型。
现在有个问题:难道就不能再对图灵机进行一些扩展,使它的计算能力更加强大?比如说原来只有一条空白纸带,现在我多给它几条纸带,原来指针只能移动一格,现在指针一次可以移动多格,做出这样的扩展,那图灵机能不能拥有更强的计算能力?
答案是不能的,因为加入的这些特性其实都可以用原来的图灵机模拟出来,这就好比js语言的语法糖,近些年来,js语言标准的推出速度越来越快了,先是es6,然后是es7,es8,现在连es10都出来了,但是这些语法糖顶多让你写代码写得简洁,并不存在有些问题你能用es10解决但是es5解决不了的,这也是像babel这类语法转化器能够存在的本质原因。
图灵完备
在上面的描述中,不知你发现了没有?一个特定的图灵机其实对应了一个特定的算法,在给定算法的情况下,我们可以把它转化成一个特定的图灵机,而一个图灵机只包含有限的状态,有限的转换规则,纸带虽然无限长,但上面的数据是有限的,总而言之,都是有限的数据,所以我们可以对它进行编码。此时,存在有一类特殊的图灵机可以接受其他图灵机的编码作为输入,然后来模拟运行这个图灵机,从而得到运行结果,这个特殊图灵机被称为通用图灵机。
其实现在的计算机就是通用图灵机的具体实现,它可以接受并运行任何一段计算机程序,这里的计算机程序可以理解为特定图灵机的编码实现。
在这里我们要做一个有趣的类比:一个特定的图灵机可以被具体地编码为一段计算机程序,通用图灵机可以模拟任何图灵机,如果有一门编程语言可以编写描述任何一段计算机程序,那么在某种程度上,通用图灵机和这门编程语言是等价的,这个时候,我们称这门编程语言是图灵完备的。
这个说法有点绕,简单来说就是通用图灵机可以模拟任何图灵机,图灵完备的编程语言可以对任何图灵机进行编码。
支持图灵完备最少需要支持哪些特性?
其实模拟图灵机所需要的条件并不苛刻,一般来讲,一门编程语言只要支持数组读写、循环和条件判断,就是图灵完备的,所以市面上几乎所有的编程语言都是图灵完备的。不过,这里有一个问题:为什么只要支持数组读写、循环和条件判断,就是图灵完备的?
- 数组读写就不用说了,数组对应图灵机里面的无限长纸带,读写对应着访问字符和擦写字符
- 循环呢?在图灵机的描述里根本就没有提到循环,为什么这里需要循环?仔细想一想,编程语言里面的循环其实对应着指针左移,假设我们把循环去掉,那么程序就会一路从头执行到尾(对应指针右移),直到最后停止,而循环在计算机底层会被翻译跳转,跳转到哪里去?当然是跳转到前头去,这不就是指针左移吗?
- 条件判断也很容易理解,如果把条件判断去掉,那状态转移没法实现,此外循环也没有办法跳出
二. typescript的类型系统是图灵完备的
上面铺垫了很多,终于来到激动人心的时刻,接下来我们将证明typescript的类型系统是图灵完备的。 在这里,我将假设你有最基本的typescirpt类型系统知识。
1. 条件判断
在typescript的类型系统中,有一个关键词extends很有用,准确地来讲,extends在typescript里有两种用法,一种是用于类的继承,比如
class A extends B {
}
另外一种用法是用于判断类型T的变量是否可以赋值给类型为U的变量,如果可以,则返回类型X,否则是Y(这个用法就类似js里面的三元运算)
T extends U ? X : Y
由于typescript还支持字面类型(所谓字面类型就是一个常量就是一个类型,比如说number属于一般类型,而常量1可以单独作为一个类型),所以这个关键词在typescript的类型编程中非常有用。除了可以用它来判断一个类型是否是另外一个类型的子类,还可以用来判断两个字面类型是否相同,比如type a = 1 extends 1 ? true : false,这个表达式里面的1,true,false都是字面类型,因为两个1相同,所以表达式会返回第一个类型,类型a便是字面类型true。因为extends既可以用来判断两个类型是否存在继承关系,还可以判断两个字面类型是否相同,所以它比js中判断是否相等的运算符更强大。
2. 无限长的纸带
typescript的类型可以递归定义:
type Node = {
prev: Node;
item: any;
}
发现了没有?其实这跟链表的定义很类似,所以我们可以用这个方式来实现一个栈,
type StackLike{
prev: StackLike;
item?: any;
}
type EmptyStack = {
prev: EmptyStack
}
type PushStack<T, Stack extends StackLike> = {
prev: Stack;
item: T;
}
type PopStack<Stack extends StackLike> = Stack['prev']
type PeekStack<Stack extends StackLike> = Stack extends {item: infer T} ? T : never
/**
* 在这里的定义实现当中,我们用到了typescript另外一个高级特性:infer,
* infer表示推断类型, infer T表示把推断出来的类型赋值给T。
* 比如说在定义了PeekStack之后,可以这样调用`type a = PeekStack<{item:number}>`,
* typescript会把`{item:number}`和`{item: infer T}`进行匹配推断,
* 很明显是可以推断的,T应当是类型number。
* 但如果这样调用`type b = PeekStack<{item1: number}>`,item1和item无法匹配,所以extends会返回第二个类型,也就是never。
*/
在这个实现当中,StackLike表示的是栈中一个节点,而且是栈顶。由于压栈(PushStack)可以无限进行下去,所以我们可以理解为一条单向无限长的纸带,两个栈加一块不就是一条双向无限长的纸带吗?
3.循环
在typescript的类型系统中没有循环的概念,但是我们可以用递归来模拟循环。比如
type Bottom<Stack extends StackLike> =
PeekStack<PopStack<Stack>> extends never ?
PeekStack<Stack> : Bottom<PopStack<Stack>>
在定义中,我们递归调用了自身定义,extends用于条件判断,避免无限递归下去。你能看出这段表达式的含义?
事实上,上面那行代码会被typescript的类型检查器报错,但是有个变通的方法可以实现相同的功能:
type Bottom<Stack extends StackLike> = {
'true': PeekStack<Stack>;
'false': Bottom<PopStack<Stack>>;
}[PeekStack<PopStack<Stack>> extends never ? 'true' : 'false'];
在这里用到了typescript的另外一个高级特性:映射类型,说白了,就是跟js的object一样,可以定义一个包含多个键值对的object,然后根据键名取出相应的东西,在js中是具体的值,在ts的类型系统中则是类型。而在定义映射类型时,递归调用自身不会被报错。
根据上面的论述,我们证明了typescript的类型系统满足支持图灵完备所需的三个特性,所以typescript的类型系统是图灵完备的。
三. 利用typescript的类型系统实现四则运算
既然typescript的类型系统是图灵完备的,那么理论上其他编程语言能做的,typescript的类型系统也能做,为了能简单证明这一点,下面将用ts的类型系统实现四则运算。
1.实现自然数系统
为了实现四则运算, 最起码地,得需要一个数字系统, 虽然typescript的类型系统支持数字字面类型,比如说可以这样写
type a = 1;
type b = 2;
但是我们不能简单地直接借用过来,因为字面类型和字面类型之间没有任何关系,我们不能对字面类型做出任何操作,比如这样写type a = 1 + 1会直接报错。
为了解决这一问题,我们只能从头开始实现一个自然数系统,想一想,自然数是怎么定义的? 这里,我们将借用皮亚诺公理来定义自然数,首先定义一个数为0,然后把1看成是0的后继,把2看成1的后继,发现了没有?这和之前的栈的实现很类似,所以自然数系统又可以用递归定义来实现。
// 定义自然数的结构
type Num = {
prev?: Num;
isZero: 'true' | 'false';
}
// 直接定义0
type Zero = {
isZero: 'true';
}
// 获取一个数的后继,和压栈类似
type Next<T extends Num> = {
prev: T;
isZero: 'false';
}
// 获取这个数的上一个数,和弹栈类似
type Prev<T extends Num> = T['isZero'] extends 'true' ? T['prev'] : never
2.实现自然数的加减乘除
在定义好自然数后,实现加减乘除就不难了
2.1 自然数的加法
加法可以理解为后继的重复,1+2,理解为取1的后继的后继,很明显需要循环来实现,但ts类型系统没有循环,但可以用递归来实现。
type Add<T1 extends Num, T2 extends Num> = {
'true': T1,
'false': Add<Next<T1>,Prev<T2>>
}[T2['isZero']]
这里的边界条件是判断T2是否为0,如果是0,则直接返回T1,如果不是,则取T1的后继,取T2的前继,再递归调用直到T2为0
2.2 自然数的减法
在做减法时可以注意到这样一个现象:a-b = (a-1) - (b-1),所以在递归实现中,我们不停地取T1、T2的前继,直到其中某个数为0。不过值得注意的是,自然数的减法不能出现负数,必须保证被减数要大于等于减数。
type Sub<T1 extends Num, T2 extends Num> = {
'true': T1,
'zero': n0,
'false': Sub<Prev<T1>, Prev<T2>>,
}[IsZero<T1> extends 'true' ? 'zero' : IsZero<T2> extends 'true' ? 'true' : 'false']
2.3 自然数的乘法
加法是后继的重复,而乘法是加法的重复,实现过程与加法类似,只不过多了一个累加器。
type Mul<T1 extends Num, T2 extends Num, Acc extends Num = Zero> = {
'true': Acc,
'false': Mul<Prev<T1>, T2, Add<T2, Acc>>,
}[IsZero<T1>]
2.4 自然数的除法
除法和乘法一样,是减法的重复,不过要注意除数不能是0,结果是向下取整的自然数。
type Div<T1 extends Num, T2 extends Num, Acc extends Num = n0> = {
'error': never,
'true': Acc,
'false': Div<Sub<T1, T2>, T2, Next<Acc>>
}[IsZero<T2> extends 'true' ? 'error' : IsGreaterThen<T2, T1> extends 'true' ? 'true' : 'false']
3.实现自然数的四则混合运算
这个部分内容稍微有点复杂,首先来看看实现四则混合运算的算法,
3.1 四则混合运算的算法
算法分为两个过程:1.是把中缀表达式转换成后缀表达式,2.对后缀表达式进行运算。
- 中缀式转化成后缀式的具体流程如下:
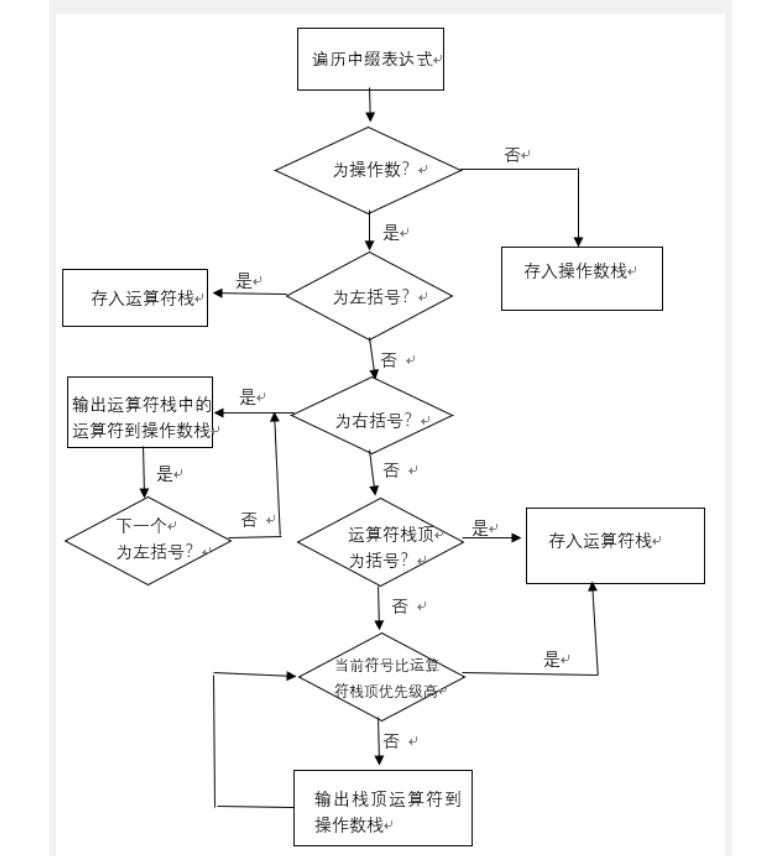
操作数栈里面的数据就是最终结果。
- 后缀式的计算就比较简单了
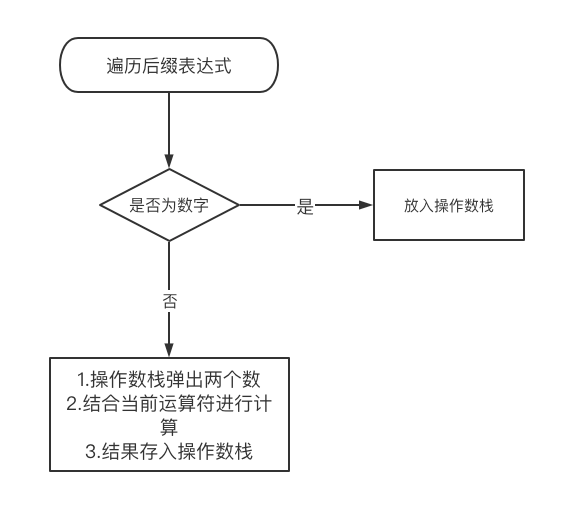
3.2 用typescript的类型系统实现算法
基本思路:
- 把算法分解成一系列的子过程:把程序所要用到的变量全部列举出来,记为Q1, Q2, ..., Qn, 此外再加一个状态RunState(运行时状态),在这里,我们用映射类型和RunState来处理程序跳转。
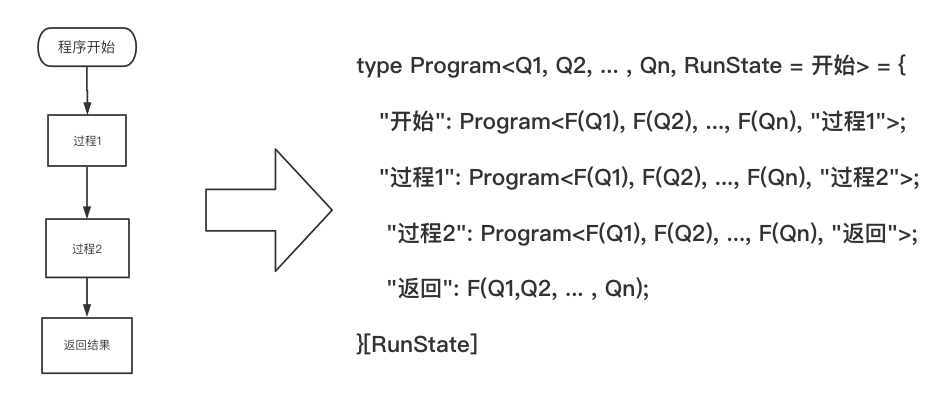
程序的本质是操作数据,因为typescript的类型系统不能改变变量的值,它只能接受原来的变量,然后输出新的变量值,在每个子过程里,我们用一个函数F来代表具体的计算过程,它接受原来的Q,输出新的Q,同时改变RunState的值,以便让程序跳转。
- 实现条件判断
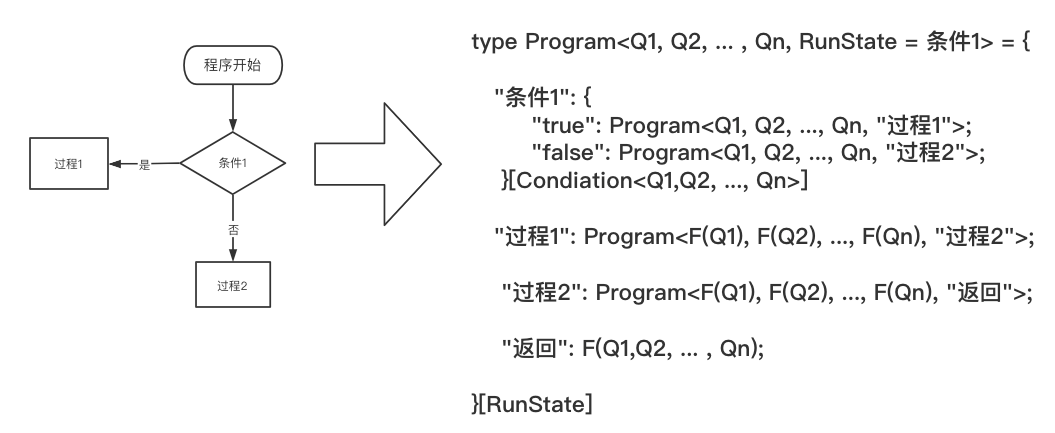
- 循环:所有的循环会被转化成递归实现

至此,根据上面的思路,我们可以把所有的算法用typescript的类型系统实现一遍。
4. typescript的类型系统是纯正的函数式编程语言
准确来讲,是函数式编程语言的子集
1. 无法改变变量的值
类型确定下来了,就无法再改变了,只能创造新的类型
2. 没有循环,只有递归
原因:一是不能改变变量的值,二是循环的表达能力不如递归。