系统聚类：就是层次聚类

import_random
1,256 阅读6分钟 
1/前言
    在进行机器学习时，我们往往要对数据进行聚类分析,例如kmeans聚类，kmeans++聚类
    聚类，物以类聚，人以群分，
    说白了就是把相似的样品点/数据点进行归类，这样一个数据集合就会被分成几类。
   
    本文要介绍的就是系统聚类法，以及如何用python来进行系统聚类分析。
     
2/系统聚类简介
    系统聚类法，又叫分层聚类法，是目前最常用的聚类分析方法。
    其基本步骤如下：
      <1>数据集合中有n个数据点，先将这n个数据点看作n类，也就是一个数据点是一类，
      <2>然后将最相似的两类合并为一个新的类，这样就得到n-1个类，
      <3>接着从中再找出最接近的两个类，让其进行合并，这样就变为n-2个类，
      <4>让此过程持续进行下去，最后所有的数据点都归为一类，
      <5>把上述过程绘制成一张图，这个图就称为聚类图，从图中再决定分为多少类。其大致过程如图1所示。
             


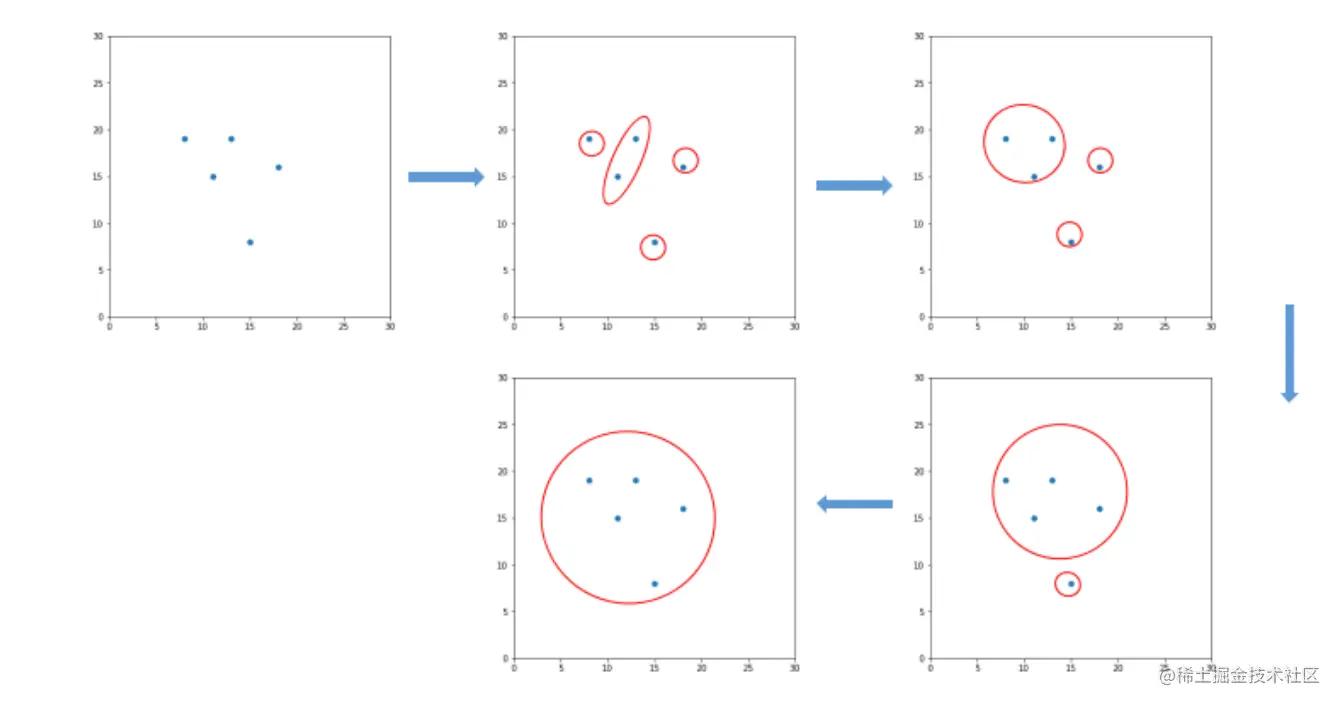
        在这里我们要确定各个数据点的相似度，才能将其归类，那么如何确定其相似度呢？通常我们用的方法是计算数据点之间的距离，然后再根据距离判定2个数据点是否是相似的。这里我们根据距离来分类，同样也是有几种方法的，比如最短距离法、最长距离法、重心法、类平均法以及ward法。下面我们对这几种方法进行一个简单的介绍。
     
3/确定相似度的几种方法
     <1> 最短距离法:
           最短距离法就是从两个类中找出距离最短的两个样品点，如图2所示。点3和点7是类G1和类G2中距离最短的两个点。计算公式如图4所示。


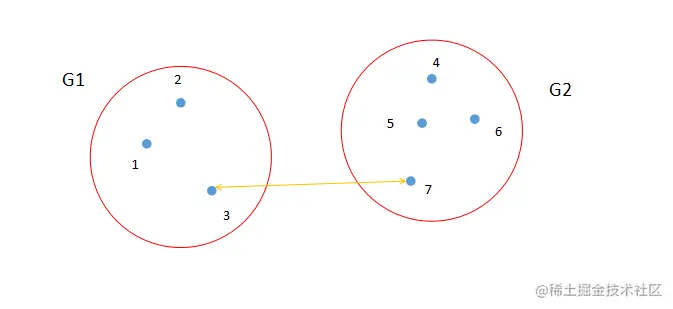
     <2> 最长距离法
           最长距离法就是从两个类中找出距离最长的两个样品点，如图3所示。点1和点6是类G1和类G2中距离最长的两个点。计算公式如图4所示。


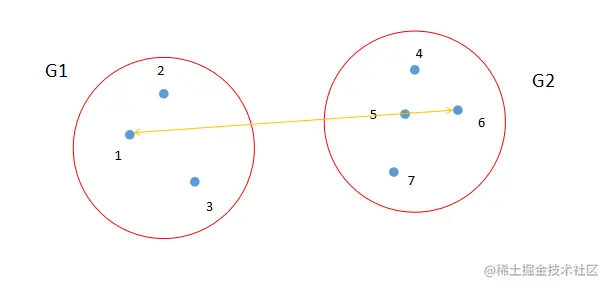
     <3> 重心法
            从物理的观点看，一个类用它的重心，也就是类样品的均值，来做代表比较合理，类之间的距离也就是重心之间的距离。若样品之间用欧氏距离，设某一步将类G1与G2合并成G3，它们各有n1、n2、n3个样品，其中n3=n1+n2，它们的重心用X1、X2和X3表示，则X3=1/n3(n1X1+n2X2)。重心法的计算公式参考图4。
     <4> 离差平方和
                 离差平方和法又叫Ward法，其思想源于方差分析，即如果类分得正确，同类样品的离差平方和应当较小，类与类之间的离差平方和应该较大。计算公式如图4所示。
                 
4/实例：用python实现系统聚类分析
    # 导入各种库
    import numpy as np
    from matplotlib import pyplot as plt
    from scipy.cluster.hierarchy import dendrogram, linkage
             
    # 接下来是生成数据集。我们这次用的数据集是随机生成的，数量也不多，一共15个数据点，分为两个数据簇，一个有7个数据点，另一个有8个。之所以把数据点数量设置这么少，是因为便于看清数据分布，以及后面画图时容易看清图片的分类。
    # 这里我们设置一个随机状态，便于重复试验。然后利用这个随机状态生成两个变量a和b，这两个变量就是前面说过的数据簇，a有7个数据点，b有8个，a和b都是多元正态变量，其中a的均值向量是[10, 10]，b的均值向量是[-10, -10]，两者协方差矩阵是[[1, 3], [3, 11]]。这里要注意的是协方差矩阵要是正定矩阵或半正定矩阵。然后对a与b进行拼接，得到变量data。
    state = np.random.RandomState(99) #设置随机状态
    a = state.multivariate_normal([10, 10], [[1, 3], [3, 11]], size=7)  #生成多元正态变量
    b = state.multivariate_normal([-10, -10], [[1, 3], [3, 11]], size=8)
    data = np.concatenate((a, b)) #把数据进行拼接
             
    # 接下来要绘制数据点的分布。代码如下。
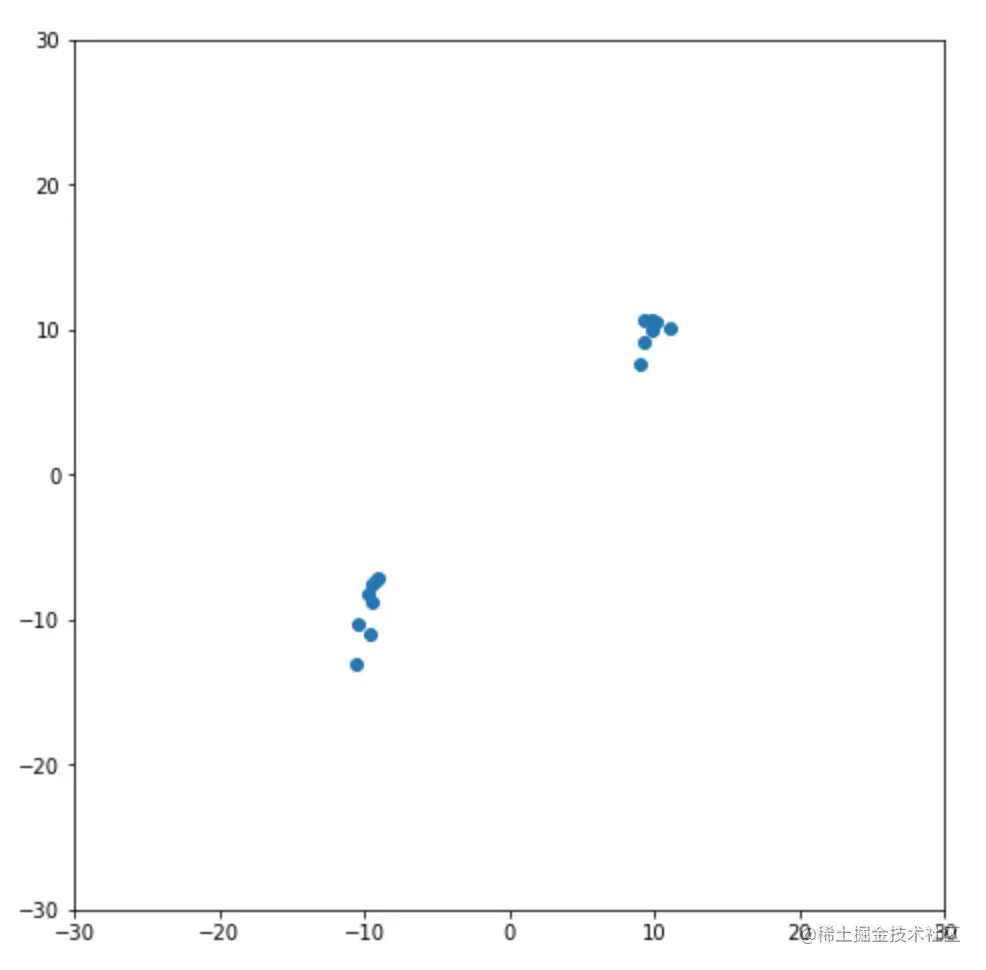
    这里代码比较简单，不再赘述，主要说一下ax.set_aspect('equal')这行代码，因为matplotlib默认情况下x轴和y轴的比例是不同的，也就是相同单位长度的线段，在显示时长度是不一样的，所以要把二者的比例设为一样，这样图片看起来更协调更准确。所绘制图片如图5所示，从图中可以明显看到两个数据簇，上面那个数据簇大概集中在坐标点[10, 10]附近，而下面那个大概集中在[-10, -10]附近，这和我们设置的是一样的。从图中可以很明显看出，这个数据集大概可以分为两类，即上面的数据簇分为一类，下面的数据簇分为另一类，但我们还要通过算法来计算一下。
     fig, ax = plt.subplots(figsize=(8,8)) #设置图片大小
     ax.set_aspect('equal') #把两坐标轴的比例设为相等
     plt.scatter(data[:,0], data[:,1])
     plt.ylim([-30,30]) #设置Y轴数值范围
     plt.xlim([-30,30])
     plt.show()
             


     #数据处理，数据处理只有这一行代码，非常简单
     z = linkage(data, "average") #用average算法，即类平均法
              


    # 绘制图
     fig, ax = plt.subplots(figsize=(8,8))
     dendrogram(z, leaf_font_size=14) #画图
     plt.title("Hierachial Clustering Dendrogram")
     plt.xlabel("Cluster label")
     plt.ylabel("Distance")
     plt.axhline(y=10) #画一条分类线
     plt.show()
             


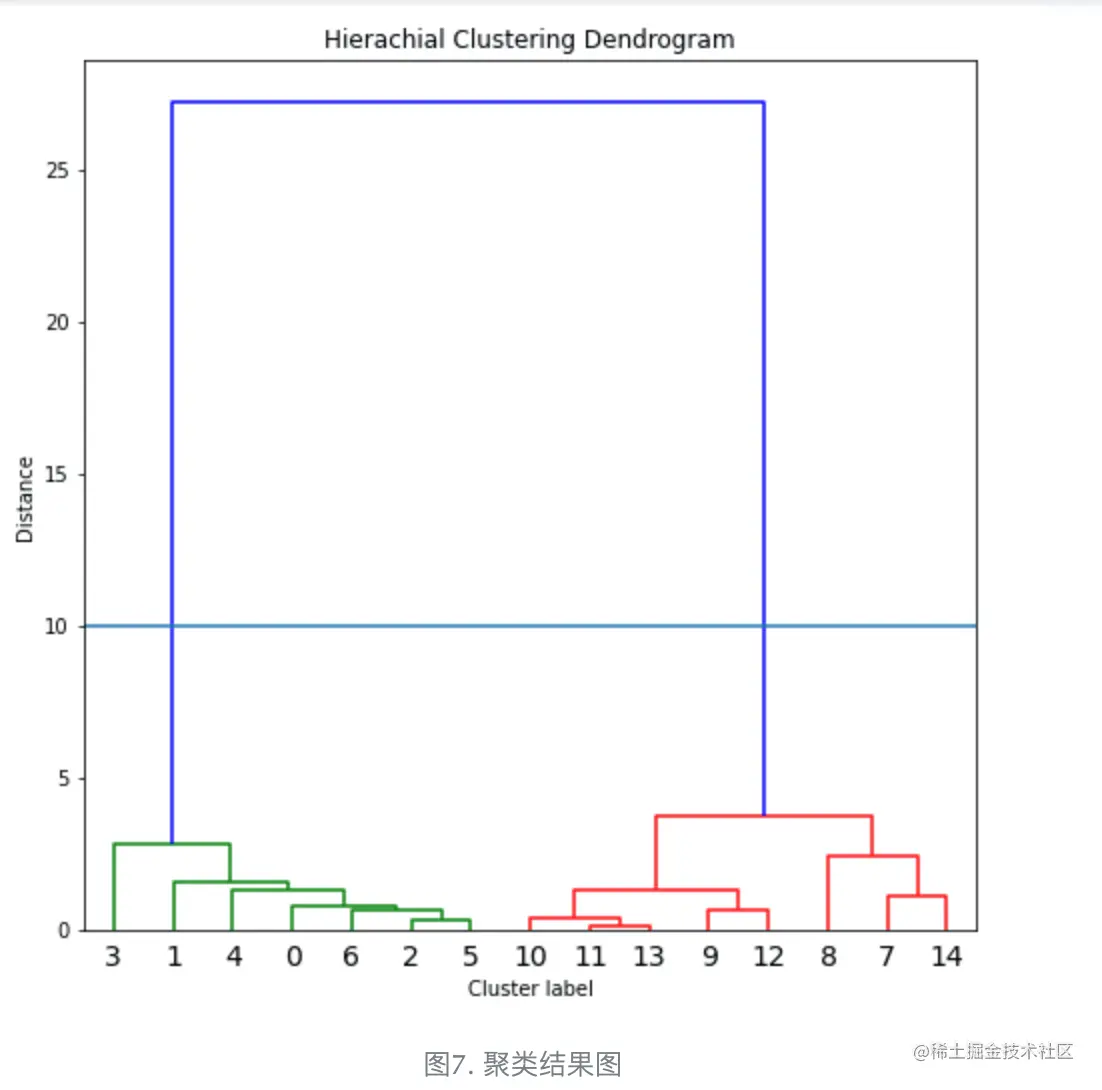
4/ 总结
   <1>从图中可以看出，这15个点可以分为两类，
      前面绿色的线连接的点代表一类，即点0到点6这7个点，
      后面红色的线连接的点代表第二类，即点7到点14这8个点。
      我们可以看到这个划分结果是非常正确的，和我们当时的设定是一样的。
   
   <2>系统聚类法的算法比较简单，实用性非常高，是目前使用最广泛的聚类方法，
      但该方法在处理极大数据量时会有所不足，所以最好配合其他算法来使用，
      同时使用者在使用时要根据自己的情况，来选择合适的距离计算方法。
      本文主要用类平均法来进行聚类操作，因为这个数据集非常简单，所以用其他距离计算方法得到的结果和这个是一样的。
      如果数据量比较大时，最终不同距离计算方法得到的结果可能不同，所以使用者要根据自己的情况来进行选择。
avatar
文章
阅读
粉丝