写了几种基本的计算递归时间复杂度的方法,每种方法都带了一个例题,这些都是笔试中出现过的题目,在这里做一个记录。
master公式解法
1.某算法的时间复杂度递归公式为
T(n)=1,n=1
T(n)=4T(n/2)+n,n>1
则它的总时间复杂度为:
A.O(n) B.O(logn) C.O(nlogn) D.O(n^2)
这一题可以使用master公式(也叫主方法,主定理)求解。
先上一个公式
- N 表示问题的规模
- a 表示一次递推的子问题的数量
表示每个子问题的规模,每个子问题的规模要一样(这里的一样不是绝对的一样,比如把问题规模N除以2,分成两个子问题,这就是一样)
表示递归以外进行的计算的时间复杂度
在这个题目中问题规模就是n,a是4,b是2,d是1,所以就是,其实跟题目给的递推公式是一样的哈,所以再遇到这种题就不用算这一步了。
然后求递归的时间复杂度,再上一个公式
当时,时间复杂度为O(n^
)
当时,时间复杂度为O((n^d)*
)
当时,时间复杂度为O(n^d)**
在本题中因为d = 1 < ,所以时间复杂度为O(n^2)
公式记忆:我们实际上是比较n^和
,如果他们不等,那么时间复杂度就取他们中的较大者,如果他们的相等,那么我们就将他们的任意一个乘以logn就可以了
这里要特别注意!!!这种方法是对于分治问题最好的解法。如果子问题的规模不一样是不能用这个公式的,并且a >=1, b >1。分治问题就是一个规模为N的问题被分成规模均为N/b的a个子问题,递归地求解这a个子问题,然后通过对这a个子问题的解的综合,得到原问题的解。
迭代法
2.设某算法的时间复杂度函数的递推方程是 T(n) = T(n - 1) + n(n 为正整数)
及 T(0) = 1,则该算法的时间复杂度为( )。
A.O(log n) B.O(n log n) C.O(n) D.O(n^2)
迭代法就是把方程的右边展开,直到没有可以迭代的项为止。
在这一题中
T(n) = T(n - 1) + n
= T(n - 2) + n + n - 1
= T(n - 3) + n + n - 1 + n - 2
= ...
=T(0) + n + n - 1 + n - 2 + ... + 1
=n(n + 1)/2
所以他的时间复杂度是O(n^2)。一般来说这种问题应该遇到的比较多。
递归树
3.以下计算斐波那契数列的函数时间复杂度为()
int Fib(int n)
{
if(n==0)
return 0;
else if(n==1)
return 1;
else
return Fib(n-1)+Fib(n-2)
}
A.O(nlogn) B.O(n^2) C.O(n) D.O(2^n)
如果n = 5 的话,我们可以画出这样一个完全二叉树
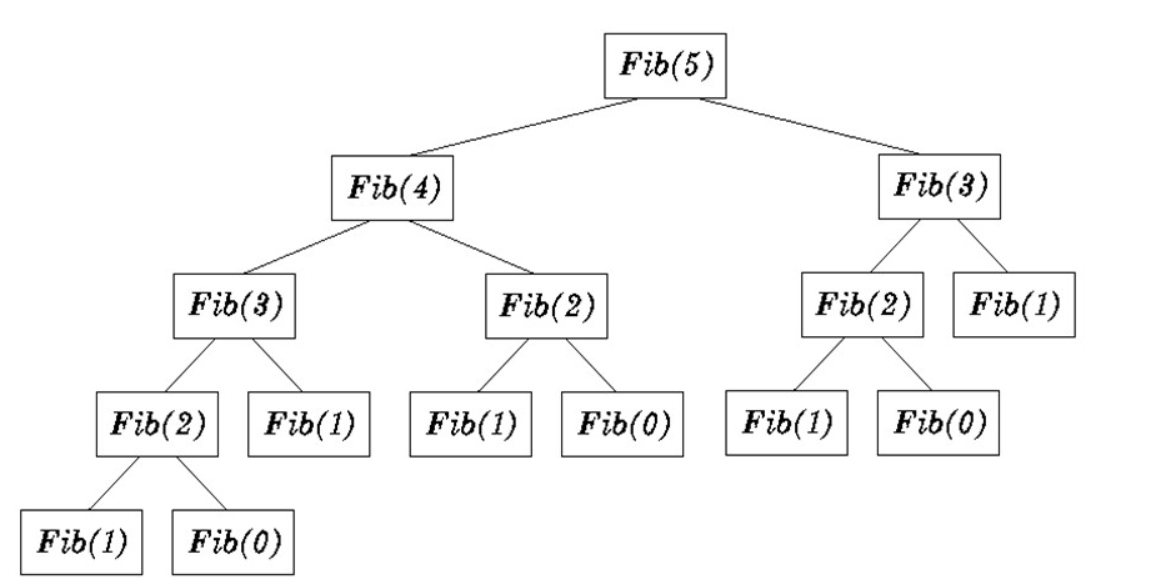
画递归树我们可以很明先地看出这个算法的缺陷,Fib(3)出现了2次,也就是这个操作进行了2次,Fib(2)出现了3次就是Fib(2)计算了两次,这里进行了多次重复计算。想优化的话,比如我们可以把这些中间值给存起来,用的时候直接取,不用进行计算。
递归时间复杂度的本质
4.下面代码的时间复杂度是()
int foo(int n) {
if (n <= 1) return 1;
return n * foo(n - 1);
}
A.O(log(n)) B.O(n) C.O(n * log(n)) D.O(n^2)
有其他的方法计算递归的时间复杂度,但是也不能忘记计算时间复杂度的本质,递归的时间复杂度就是递归的次数 * 每次递归中的操作次数,这一题是计算n的阶乘,递归了n次,每次进行乘法操作时间复杂度是O(1),所以他的时间复杂度就是O(n)