前言
话不多说,肝就完事。不过感觉在掘金上写算法没啥人看……也有可能是我太菜了吧。
JZ6 旋转数组的最小数字
题目
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
解法一
恕我直言,好像没什么意思啊,第一直觉,O(n)扫一遍
while(line=readline()){
//将json字符串转换为JavaScript值或对象
let arr = JSON.parse(line);
print(minNumberInRotateArray(arr));
}
function minNumberInRotateArray(rotateArray)
{
// write code here
var len = rotateArray.length;
if(len == 0)
return 0;
var min = rotateArray[0];
for(var i = 0; i < len; i++)
{
if(min > rotateArray[i]){
min = rotateArray[i];
}
}
return min;
}
function minNumberInRotateArray(rotateArray)
{
return Math.min(...rotateArray)
}
解法二
仔细观察下题目,会发现有着某种设定,输入的总是经过一次旋转的数组,也就是说会形成从小到大然后一个跌越再从小到大这样的规律。而我们要找的便是中间那个跌越点,就是整个数组的最小值。
也就是说实际上最小的元素就是两个子数组的分界线。
既然两个子数组是有序的,可以用二分查找来找。
- 我们用两个指针left,right分别指向数组的第一个元素和最后一个元素。按照题目的旋转的规则,第一个元素应该是大于最后一个元素的
- 找到数组的中间元素。
(1)array[mid] > array[high]:
出现这种情况的array类似[3,4,5,6,0,1,2],此时最小数字一定在mid的右边。
low = mid + 1
(2)array[mid] == array[high]:
出现这种情况的array类似 [1,0,1,1,1] 或者[1,1,1,0,1],此时最小数字不好判断在mid左边
还是右边,这时只好一个一个试 ,把范围缩小一步
high = high - 1
(3)array[mid] < array[high]:
出现这种情况的array类似[2,2,3,4,5,6,6],此时最小数字一定就是array[mid]或者在mid的左
边。因为右边必然都是递增的。
high = mid
代码如下:
while(line=readline()){
//将json字符串转换为JavaScript值或对象
let arr = JSON.parse(line);
print(minNumberInRotateArray(arr));
}
function minNumberInRotateArray(rotateArray)
{
// write code here
var len = rotateArray.length;
if(len == 0) return 0;
var left = 0;
var right = len - 1;
while(left < right)
{
var mid = parseInt((left + right) / 2);
if(rotateArray[mid] > rotateArray[right])
{
left = mid + 1;
}else if(rotateArray[mid] < rotateArray[right])
{
right = mid;
}else{
right--;
}
}
return rotateArray[left];
}
JZ7 斐波那契数列
题目
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。 n<=39
解法一
一个比较丑陋的解法,直接依照公式。 F(1)=1,F(2)=1, F(n)=F(n - 1)+F(n - 2)
function Fibonacci(n)
{
// write code here
if(n == 0) return 0;
if(n == 1) return 1;
if(n == 2) return 1;
var ret = 0;
ret = Fibonacci(n-1) + Fibonacci(n-2);
return ret;
}
解法二
一种动态规划方法.详细看注释
function Fibonacci(n)
{
// write code here
if(n == 0) return 0;
if(n == 1) return 1;
if(n == 2) return 1;
let a = 0, b = 1;
while(n--)
{
b += a;//形成新的后值
a = b - a;//相当于原来b的值
}
return a;
}

还有一种从榜上看到的写法:
function Fibonacci(n)
{
// write code here
const arr=[0,1]
for(let i=2;i<=n;i++){
arr[i]=arr[i-1]+arr[i-2]
}
return arr[n]
}
JZ8 跳台阶
题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
解法一
很典型的递归啦,一般都练到过吧伙伴们?说下思路,一次跳两级或者一级,那么我们就作为青蛙站在某个台阶上思考蛙生,我只有两种可能来到这里:1.从我下面一级跳上来的2.从我下面两级那里跳上来的。
得到这样的表达式:
if(n == 1) return 1;
if(n == 2) return 3;
F(n) = F(n-1) + F(n-2);
代码如下:
function jumpFloor(number)
{
// write code here
if(number == 1) return 1;
if(number == 2) return 2;
let ret = 0;
ret = jumpFloor(number - 1) + jumpFloor(number - 2);
return ret;
}
解法二
同样可以用动态规划进行优化。
function jumpFloor(number)
{
// write code here
if(number == 1) return 1;
if(number == 2) return 2;
let ret = 0;
let a = 1, b = 2, c = 0;//分别表示跳上一级、二级有几种方法 三级的还没算,每次移步都算下一步的值
while(number > 2)
{
c = a + b;
a = b;
b = c;
number--;
}
return c;
}

榜上有一种写法:
function jumpFloor(number) {
let dp = []
dp[0] = 1
dp[1] = 2
for (let i = 2; i < number; i++) {
dp[i]=dp[i-1]+dp[i-2]
}
return dp[number-1]
}
JZ9 变态跳台阶
题目
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解法
哦豁,真的变态。但是其实很简单啦。
每个台阶可以看作一块木板,让青蛙跳上去,n个台阶就有n块木板,最后一块木板是青蛙到达的位子, 必须存在,其他 (n-1) 块木板可以任意选择是否存在(存在即是选择了踏上这块跳板),则每个木板有存在和不存在两种选择,(n-1) 块木板 就有 [2^(n-1)] 种跳法,可以直接得到结果。
所要求的序列为:0,1,2,4,8,16,……
function jumpFloorII(number)
{
// write code here
if(number == 1) return 1;
return jumpFloorII(number-1)*2;
}

JZ10 矩形覆盖
题目
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
比如n=3时,2*3的矩形块有3种覆盖方法:
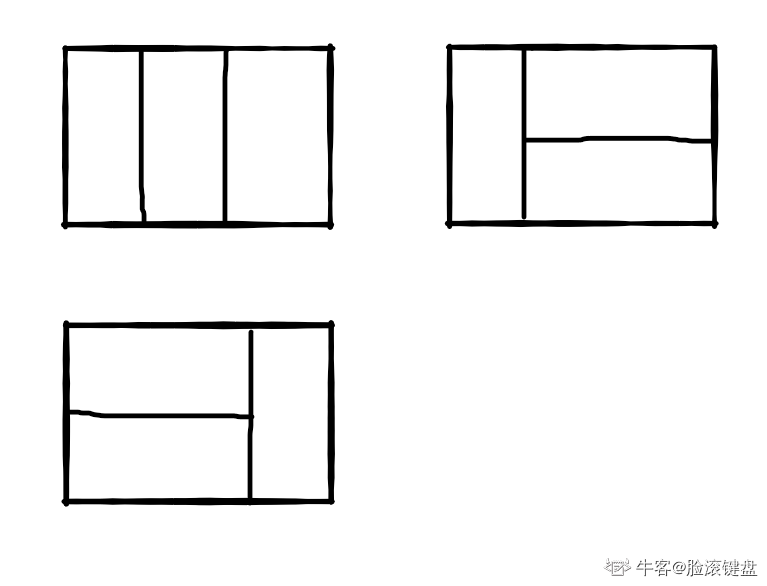
解法
这里主要是思路的问题,我一开始用没想明白,分奇偶解决,但是不知为啥一直溢出。后面重新分析了一下。
n = 1时 return 1;
n = 2时,只有||和=两种情况;
n = 3时,有上面三种情况;
n = 4时,有从n=3出发的变形情况:和=||和||||和|=|这样三种情况,所以只在n=3的基础上往后面添加了一个竖着的。
从n=2出发的变形情况||=,==,=||和||||(这两种重复了),所以只在n=2的基础上往后面添加了两个横着的情况。
这样的话n=4的情况就是和n=2的情况+n=3的情况数量一致。
其他情况都是类似的。可以自然得到这样一个规律,f(n) = f(n-1) + f(n-2),就是我们之前做过的斐波那契数列了。
function rectCover(number)
{
// write code here
if(number == 0) return 0;
if(number == 1) return 1;
if(number == 2) return 2;
let a = 1, b = 2;
while(number-- >= 2)
{
b += a;
a = b - a;
}
return a;
}
