《剑指Offer》JS题解——JZ1~5

giria
266 阅读8分钟

前言

第一次刷这个系列，以前ACM的时候刷了一些leetcode，都没做什么记录。秋招前就做个刷题加算法记录吧。解法纯属个人理解，如若有错望指出。

语言基本用的JS，算作自我练习。

#JZ1 二维数组中的查找

题目：

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解法一

最直观的解法，大部分人都能很快写出来吧。直接暴搜，稍微利用一下递增的信息。

对于每个一维数组来说，最后一个是整个数组的最大值。同时又满足垂直递增，因此可以在搜索前判断一下范围。

  • 如果target比一维数组的最后值还要大，那就没必要搜它了。
  • 同理，target比一维数组的第一个数字还要小，就不用管了。
//通过简单判断进行搜索范围划定，降低复杂度
function Find(target, array)
{
    // write code here
    var num = array.length;
    var nlength = array[0].length;
    for(var i = 0; i < array.length; i++)
    {
        if(array[i][nlength] < target || array[i][0] > target)//范围划定
        {
            continue;
        }else{
            for(var j = 0; j < nlength; j++)
            {
                if(target == array[i][j])
                {
                    return true;
                }
            }
        }
    }
    return false;
}

效率如下：

解法一效率
不过这就没二分搜索什么事了，这题八成要考的就是这玩意儿。

解法二

利用二分搜索

关于二分搜索

二分搜索是一种基本的搜索算法，在拥有递增、递减等规律性数据结构中有重要应用。由于其简单易懂的思路、清晰的递归过程，是有序前提下不二的算法选择。

二分查找法的O(log n)让它成为十分高效的算法。不过它的缺陷却也是那么明显的。就在它的限定之上：

  • 必须有序，我们很难保证我们的数组都是有序的。当然可以在构建数组的时候进行排序，可是又落到了第二个瓶颈上：它必须是数组。

  • 数组读取效率是O(1)，可是它的插入和删除某个元素的效率却是O(n)。因而导致构建有序数组变成低效的事情。

不过是题外话了。回到本题，借用牛客网的题解图，对于一维数组的二分折半搜索图示如下：

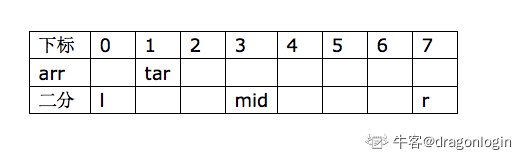
一维二分查找

假设目标tar在arr[1]处，那么我们的二分过程就是(来源为牛客网)：

  1. 设初始值：定义一个二分的开始下标为l，结束下标为r，如图所示：
  2. 二分一半，中间位置为 mid = l + （（r - l) >> 1)， val>>1, 表示val右移一位相当于val／2，相当于 l+(r-l)/2,这样的写法是防止溢出。如果写成 mid = （l+r)/2; l+r可能会溢出。
  3. 如果 tar == arr[mid]，说明找到tar
  4. 比较：如果tar > arr[mid], 说明tar在区间[mid+1, r]中，l = mid + 1
  5. 如果tar < arr[mid]，说明tar在区间[l, mid-1]中, r = mid - 1

所以进一步改进一维数组的搜索方式：

function Find(target, array)
{
    // write code here
    var num = array.length;
    var nlength = array[0].length;
    for(var i = 0; i < num; i++)
    {
        if(array[i][nlength] < target || array[i][0] > target)//范围划定
        {
            continue;
        }else{
            var low = 0;
            var high = nlength - 1;
            while(low <= high)
            {
                var mid = parseInt((low + high) / 2);
                if(target < array[i][mid])
                {
                    high = mid-1;
                    
                }else if(target > array[i][mid])
                {
                    low = mid+1;
                }else{
                    return true;
                }
            }
        }
    }
    return false;
}

解法三

拓展到二维数组还有一种类似于动态规划（？）的算法。牛客网中有把基标定在右上角的解析，那我就定在左下角来分析吧。

二维折半
根据题意，我们能知道val右侧均> val，其上侧均< val，假设俺们的target位于arr[1][2]处。

首先进行tar与当前val的判断，若tar > val，说明tar必定不在小于val的区域内，所以val可以右移进入下一层递归了。arr[3][0] -> arr[3][1]

大于情况
若tar < val说明，tar不在大于val的区域内，val可以上移了。arr[3][]

小于情况
把val的位置横向看做x坐标，纵向看做y坐标，就可以变相得出：

  • 若tar > val, x++（val右移）
  • 若tar < val, y++（val上移）

复杂度分析

时间复杂度：O(m+n) ，其中m为行数，n为列数，最坏情况下，需要遍历m+n次。

空间复杂度：O(1)

function Find(target, array)
{
    var num = array.length;
    var nlength = array[0].length;
    for(var x = 0, y = 0; x < nlength && y <= num - 1; )
    {
        if(target < array[num - 1 - y][x])//注意这里要-1以及在二维数组中需要进行坐标切换
        {
            y++;
        }else if(target > array[num - 1 - y][x])
        {
            x++;
        }else
        {
            return true;
        }
    }
    return false;
}

二分方法
啧看起来提升效果不多呀。顺便说如果想在牛客网上刷运行时间的话，最好自己写处理函数，会快很多。

在函数前加上这个：

while(line=readline()){
    var index = line.indexOf(',');
    var left = parseInt(line.substring(0,index));
    var right = JSON.parse(line.substring(index+1));
    print(Find(left,right))
}

登登登~自个儿parse就是比内部过输入数据模式切换快啊。

#JZ2 替换空格

题目

请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

解法

啊这，这不就是我js的大天下？一行搞定

function replaceSpace(str)
{
    // write code here
    return str.replace(/ /g, "%20")
    //str.replace(/\s/g,'%20')这样写也可以。
}

顺便说一声，如果直接用str.replace(" ", "%20")是8行的，因为replace只替换首个匹配。

#JZ3 从头到尾打印链表

题目

输入一个链表，按链表从尾到头的顺序返回一个ArrayList。

解法

先来复习下链表，长这样：

链表结构
那么只要构造一个数组，将数据每次都从头部插入（由于数据是倒着插入的，最后会得到一个正着的数组）

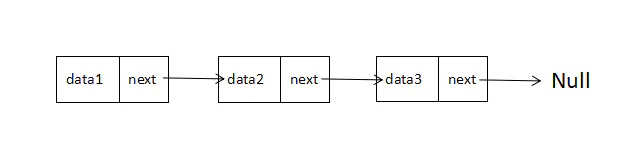
/*function ListNode(x){
    this.val = x;
    this.next = null;
}*/
function printListFromTailToHead(head)
{
    // write code here
    var arr = new Array;
    while(head != null)
    {
        arr.unshift(head.val);
        head = head.next;
    }
    return arr;
}

链表结果

这里有很多关于链表的操作，后面可以拎出来练练：JS中的算法与数据结构——链表(Linked-list)

#JZ4 重建二叉树

题目

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

解法：

复习下二叉树，如果是一棵完全二叉树长这样：

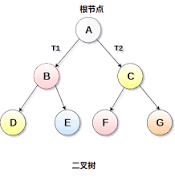
完全二叉树

前序遍历：根结点 ---> 左子树 ---> 右子树（先遍历根节点，然后左右））

中序遍历：左子树---> 根结点 ---> 右子树（在中间遍历根节点）

后序遍历：左子树 ---> 右子树 ---> 根结点（最后遍历根节点）

层次遍历：只需按层次遍历即可

思路：

  1. 根据前序遍历序列找到根节点的值（根据前序遍历规律知道第一个就是根节点了）
  2. 在中序遍历序列中找到根节点的位置
  3. 找到左子树根节点（中序遍历中根结点的前一个位置，如果存在的话，就是左子树的根结点）
  4. 找到右子树根节点（中序遍历中根结点的后一个位置，如果存在的话，就是右子树的根结点）
  5. 递归地重建子树（使用左子树的前序、中序序列构建左子树；使用右子树的前序、中序序列构建右子树）
function reConstructBinaryTree(pre, vin)
{
    // write code here
    if(vin.length == 0)
        return null;
    var ret = {};
    if(vin.length > 1)
    {
        var root = pre[0];
        var i = vin.indexOf(root);
        var left_vin = vin.slice(0, i);//根据中序遍历原理，根结点前面的一定是它下面的左子树结点们
        var left_pre = pre.slice(1, left_vin.length+1);//根据前序遍历原理，它的左子树的前序遍历，只需要从根节点之后摘出相应左子树结点个数就可以。
        var right_vin = vin.slice(i+1, vin.length);//根据中序遍历原理，根结点后面的一定是它下面的左子树结点们
        var right_pre = pre.slice(left_vin.length+1, pre.length);//后面的都是右节点的前序遍历了（因为前->左->右，而前和左已经取完了，剩下都是右了）
        ret = {
            val: root,
            left: reConstructBinaryTree(left_pre, left_vin),
            right: reConstructBinaryTree(right_pre, right_vin)
        }
    }else if(vin.length == 1){
        ret = {
            val: pre[0],
            left: null,
            right: null
        }
    }
    return ret;
}

结果

#JZ5 用两个栈实现队列

题目

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

解法

队列就是像排队一样，一个接一个，先来排队的先出去。

而栈则是像杯子一样，先进来的韭菜被压在下面，后进来的韭菜先被割走（斜眼笑）

要变成队列就很简单了呀~想象一下，这里有两个杯子，要怎样才能实现整齐地先来先被割的韭菜队列呢？

进来一系列的韭菜，在栈中他们就是

|=============================================
|（底）1号韭菜--2号韭菜--……---最后来的韭菜（顶）
|=============================================

这样的顺序，那么只要把它反过来像杯子倒水一样扣在另一个栈里，不就变成这样子了：

            ===============================================|
得到解放<---(顶)1号韭菜--2号韭菜--……---最后来的韭菜(底)      |
            ===============================================|

就可以按序倒出去了，这就是pop的实现方法了。这时候数据是存在2号栈中的，要是又有新数据来了怎么办，那就倒回1号栈中然后把新韭菜塞进来就OK了。

|=============================================
|（底）1号韭菜--2号韭菜--……---最后来的韭菜（顶）<--新来的韭菜
|=============================================

那么代码就很好写了：

var stack1 = [];//默认数据先装这里
var stack2 = [];
function push(node)
{
    // write code here
    if(stack2.length > 0)
    {
        while(stack2.length > 0)
        {
            stack1.push(stack2.pop());
        }
    }
     return stack1.push(node);
    
}
function pop()
{
    // write code here
    if(stack1.length > 0){
            while(stack1.length > 0)
            {
                stack2.push(stack1.pop());
            }
    }
    return stack2.pop();

}

运行结果

好像上算法课讲过一道更难的，忘了题目了，下次见到了补充进来吧。

avatar
文章
阅读
粉丝