OpenGL 向量与矩阵在开发过程我们涉及到图形变换，就会涉及到矩阵、向量的计算，所以本文就简单地理解一下向量跟矩阵的概

注：本文旨在记录笔者的学习过程，仅代表笔者个人的理解，如果有表述不准确的地方，欢迎各位指正！因为涉及到的概念来源自网络，所以如有侵权，也望告知！

前言

在开发过程我们涉及到图形变换，就会涉及到矩阵、向量的计算，所以本文就简单地理解一下向量跟矩阵的概念。

正文

什么是向量

从几何意义上说，向量是具有大小和方向的有向线段。在 3D 笛卡尔坐标系, 基本上⼀个顶点就是XYZ 坐标空间上的⼀个位置。⽽在空间中给定的⼀个位置，恰恰是由⼀个单独的 XYZ 定义的，⽽这这样的 XYZ 就是向量。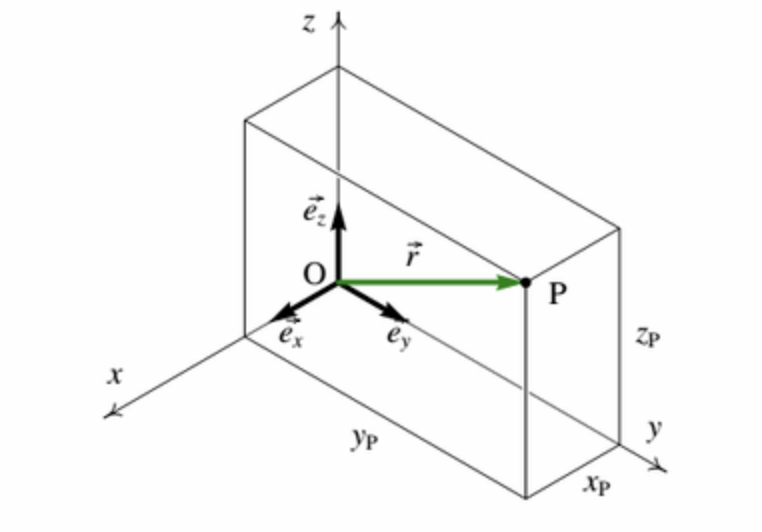

向量的点乘

向量可以进⾏加法、减法计算，但是向量⾥有⼀个在开发中使⽤价值⾮常⾼的操作，叫做“点乘”。

定义：已知两个非零向量a,b，作OA=a,OB=b，则∠AOB称作向量a和向量b的夹角，记作θ并规定0≤θ≤π。两个向量的点乘是一个标量（没有方向），记作a·b。若a、b不共线，则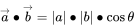。我们称为⻓度为1的向量为单位向量。

通过定义我们可以发现，2个单位向量之间进⾏点乘运算，它表示两个向量之间的夹⻆。

OpenGL运用：math3d 库中提供了关于点乘的API

//1.m3dDotProduct3 函数获得2个向量之间的点乘结果;

float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);

//2.m3dGetAngleBetweenVector3 即可获取2个向量之间夹⻆的弧度值;

float m3dGetAngleBetweenVector3(const M3DVector3f u,const M3DVector3f v);

向量的叉乘

同样向量⾥有另外⼀个在开发中使⽤价值⾮常⾼的操作，叫做“叉乘”。

定义：两个向量a和b的叉乘向量的几何表示是一个向量，记作a×b。若a、b不共线，则a×b的模是：∣a×b∣=|a|·|b|·sin〈a，b〉；a×b的方向是：垂直于a和b，且a、b和a×b按这个次序构成右手系。若a、b垂直，则∣a×b∣=|a|*|b|（此处与数量积不同，请注意），若a×b=0，则a、b平行。向量积即两个不共线非零向量所在平面的一组法向量。

简单理解，2个向量之间叉乘就可以得到另外⼀个向量，新的向量会与原来2个向量定义的平⾯垂直. 同时进⾏叉乘，不必为单位向量。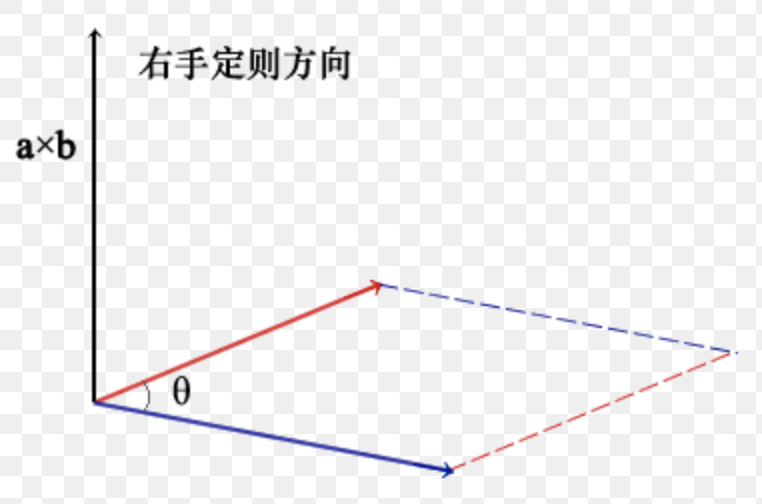

OpenGL运用：math3d 库中提供了关于叉乘的API

//1.m3dCrossProduct3 函数获得2个向量之间的叉乘结果得到⼀个新的向量

void m3dCrossProduct3(M3DVector3f result,const M3DVector3f u ,const M3DVector3f v);

什么是矩阵

定义：由 m × n 个数a_ij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。

记作：这m×n 个数称为矩阵A的元素，简称为元，数a_ij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 a_ij为(i,j)元的矩阵可记为(a_ij)或(a_ij)_{m × n}，m×n矩阵A也记作A_mn。

那么在OpenGL中我们怎么定义矩阵？在其他编程标准中，许多矩阵库定义⼀个矩阵时，使⽤⼆维数组。OpenGL的约定⾥，更多倾向使⽤⼀维数组，这样做的原因是： OpenGL 使⽤的是 Column-Major(以列为主)矩阵排序的约定。

//三维矩阵/四维矩阵的声明

typedef float M3DMatrix33f[9];

typedef float M3DMatrix44f[16];

矩阵计算

假设在空间有⼀个点，使⽤ xyz 描述它的位置，此时让其围绕任意位置旋转⼀定⻆度后，我们需要知道这个点的新的位置，此时需要通过矩阵进⾏计算。此外，矩阵只有⼀⾏或者⼀列都是合理的，只有⼀⾏或者⼀列数字可以称为向量，也可以称为矩阵。

我们知道，在OpenGL中我们将图形渲染到屏幕上，中间经历了很多矩阵变换，其中最常涉及到的变化是模型矩阵变换、视图矩阵变换、投影矩阵变化。例如下列公式:

变换顶点向量 = M_pro * M_view * M_model * V_local

变换顶点向量 = 投影矩阵 ✖ 视图变换矩阵 ✖ 模型矩阵 ✖ 顶点