树是一种非线性的数据结构, 由节点和边组成, 而每一个节点都包含键值(key)和额外的数据项. 文件系统, HTML文档以及域名体系都属于树结构的应用.
二叉树: 每个节点最多有两个子节点.
根节点: 没有父节点的节点.
叶节点: 没有子节点的节点.

1. 二叉树的实现

二叉树可以使用嵌套列表或链表的方式来实现二叉树:

class tree_node {
    public int key;
    public String data;
    public tree_node left_node, right_node;
    public String to_string() {...}
    public void insert_left() {...}
    public void insert_right() {...}
}
class tree {
    public tree_node root;
}

2. 树的应用

2.1 表达式解析

利用树结构可以对全括号表达式进行解析, 括号内的操作符作为节点, 而左右子节点分别为待操作数值:

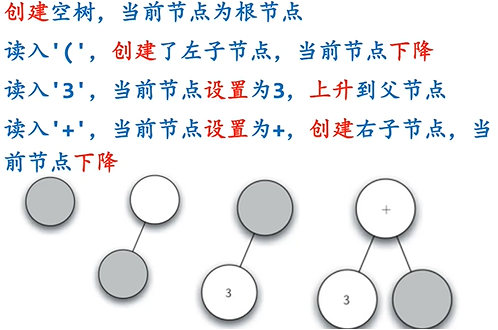
3. 二叉堆实现优先队列

优先队列PriorityQueue: 队列的一种变体, 队首元素的key值永远保持为队中最小, 和有序表的区别在于优先队列内部没有排序, 而且每次只能从队首出队. 而如果用有序表实现优先队列, 那么入队的时间复杂度将达到O(n).
二叉堆Binheap: 也就是父节点key值比子节点key值小的二叉树, 用二叉堆来实现优先队列, 就能够保证入队和出队的时间复杂度都为O(logn).
为了保证二叉堆的入堆, 出堆时间复杂度都为对数级别, 就需要尽量保证二叉堆的两枝平衡, 这样的结构称为完全二叉树, 其具体定义是叶节点只能出现在最底层和次底层:

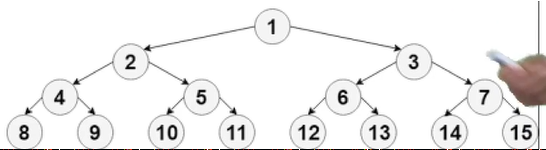
基于这样的特性, 完全二叉树可以基于非嵌套的列表来实现, 对于任何一个节点而言, 其index值乘以2即为左子节点index值... 二叉堆的插入操作: 新插入的节点只会打乱其所在路径的key顺序, 因此需要依次对比其路径上的每个父节点, 重新排序即可, 时间复杂度为O(logn);

二叉堆删除操作(优先队列出队): 二叉堆的删除同样会破坏堆次序, 因此需要比较两个子节点的大小, 较小的子节点进行上浮, 时间复杂度为O(logn);

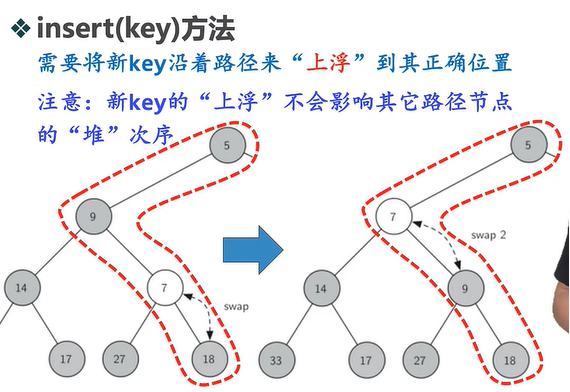
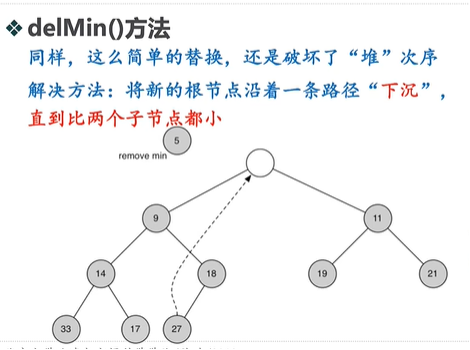
4. 二叉查找树BST

二叉查找树是一种更快实现map映射的方式, 它需要保证对于任何一个节点而言, 比它key值小的节点都出现在左子树, 比它key值大的节点都出现在右子树;

因此, 如果key列表是完全随机分布的, 那么就能保证BST的近似平衡性, 这样插入节点的操作的时间复杂度将为O(logn), 但是在最极端的情况下, BST的高度将达到n,因此插入操作的时间复杂度为O(n).

5. 二叉平衡树AVL

二叉平衡树和二叉查找树相比, 在插入新的节点时, 能够保持树的两枝尽量平衡, 也就解决了上述问题. 其具体实现方法是为每一个节点引入平衡因子的概念, 平衡印子定义为该节点左右两树的高差. 如果一个二叉树的每个节点平衡因子都为-1~1之间, 就称为二叉平衡树. 这样AVL在最差的情况下, 搜索的时间复杂度也为O(logn); 对于二叉平衡树AVL, 插入新的节点会导致整条路径上的平衡因子的变动:

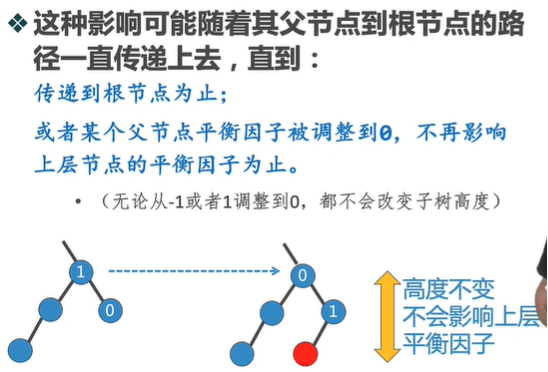
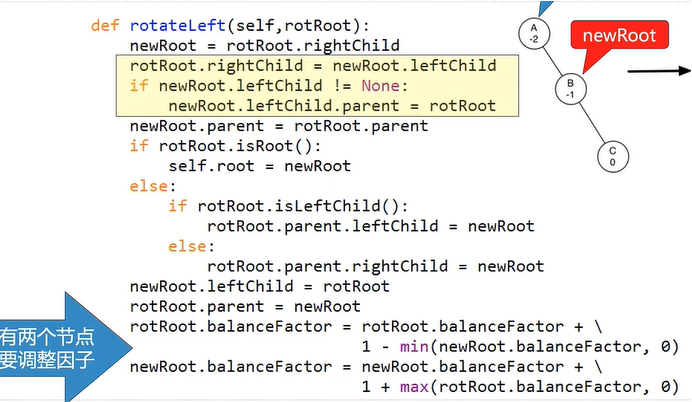
5.1 二叉平衡树的算法分析

不论是插入节点或是删除节点, 重新平衡两枝的操作与问题规模没有任何关系, 是常数级的, 因此插入与删除节点的时间复杂度仍为O(logn).

6. 哈夫曼树与哈夫曼压缩

一个关于文本文件压缩的自然思路是:** 对于出现最多的字符,尽可能用最短的二进制编码来表示**, 这样就能降低文件的占用空间. 除此之外, 还应当保证任何一个字符的编码都不能作为另一个字符编码的前缀, 防止引起歧义. 因此, 文件压缩的操作顺序是:

统计文件中各个字符出现的频率;
将字符从高频到低频排列, 为其匹配尽可能短的字符串; 哈夫曼树的结构能够适应任务2的要求: 其定义为带权路径长度最小的二叉树, 同时每一个叶节点对应一个字符, 因此不会引起编码歧义.

6.2 哈夫曼压缩的实现

// 1. 统计文件中的字符频率
while ((char_tmp = fis.read()) != -1) {
    tmp_nodes[char_tmp].weight++;
    file_len++;
}
fis.close();

// 2. 对字符进行排序，从大到小排列，同时计算出字节的种类数目
Arrays.sort(tmp_nodes);
for (i = 0; i < 256; i++) {
    if (tmp_nodes[i].weight == 0) {
        break;
    }
    Node tmp = new Node();
    tmp.Byte = tmp_nodes[i].Byte;
    tmp.weight = tmp_nodes[i].weight;
    queue.add(tmp);
}
num_chars = i;

// 3. 生成哈夫曼树并建立编码
if (num_chars == 1) {
    // 直接进行哈夫曼压缩
    oos.writeInt(num_chars);
    oos.writeByte(tmp_nodes[0].Byte);
    oos.writeInt(tmp_nodes[0].weight);
} else {
    // 3.1 建树
    this._create_tree(queue);
    root_node = queue.peek();
    // 3.2 生成哈夫曼编码
    this._huffman_code(root_node, "", map);

    // 3.3 进行哈夫曼压缩
    // 3.3.1 写入字符数量
    oos.writeInt(num_chars);
    // 3.3.2 写入编码约定
    for (i = 0; i < num_chars; i++) {
        oos.writeByte(tmp_nodes[i].Byte);
        oos.writeInt(tmp_nodes[i].weight);
    }
    // 3.3.3 写入文件长度
    oos.writeInt(file_len);
    // 3.3.4 转化
    fis = new FileInputStream(inputFile);
    code = new StringBuilder();
    while ((char_tmp = fis.read()) != -1) {
        code.append(map.get((byte) char_tmp));
        while (code.length() >= 8) {
            char_tmp = 0;
            for (i = 0; i < 8; i++) {
                char_tmp <<= 1;
                if (code.charAt(i) == 'i') {
                    char_tmp |= 1;
                }
            }
            oos.writeByte((byte) char_tmp);
            code = new StringBuilder(code.substring(8));
        }
    }
    // 当编码长度不够8位时,用0进行补齐
    if (code.length() > 0) {
        char_tmp = 0;
        for (i = 0; i < code.length(); ++i) {
            char_tmp <<= 1;
            if (code.charAt(i) == '1') {
                char_tmp |= 1;
            }
        }
        char_tmp <<= (8 - code.length());
        oos.writeByte((byte) char_tmp);
    }

20200717-树ADT