一、前言
在学习OpenGL过程中,虽然我们不需要精通里面所有的3D图形属性知识, 但是我们仍需要对它进行一些初步的了解。就如同学习iOS的时候,我们也需要去了解底层原理的实现,才能更好的去使用它。
二、向量与矩阵
GLTools库中有一个组件叫Math3d,其中包含了大量好用的OpenGL一致的3D数学和数据类型。随便我们不必亲自进行所有的矩阵和向量的操作,但我们仍需知道它是什么,以及如何运用它们。
在前文中一些绘制图元,对图形进行一些变换,就会用到矩阵/向量的计算。
2.1、向量
向量: 在我们初高中的时候就已经接触过这个名词,它表示一段带有方向、长度的线段。通常使用一个带箭头的线段来表示。
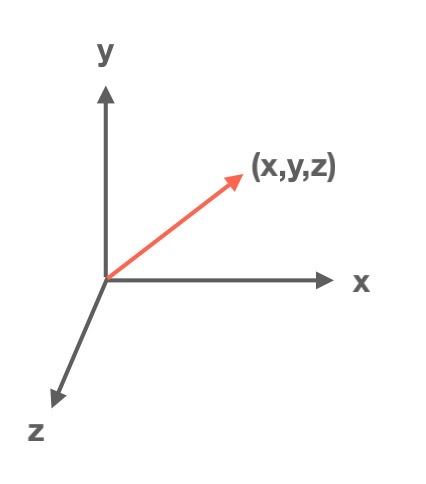
在3D笛卡尔坐标系中,一个顶点就是XYZ坐标空间上的一个位置。而在空间中给定一个位置恰恰是由一个单独的XYZ定义的。 而这样的XYZ就是向量
在x轴上的向量(1,0,0). 向量长度为1,我们称为长度为1的向量为单位向量。
向量长度的计算公式:
如果一个向量不是单位向量,而我们把它缩放到1,这个过程叫做标准化。将一个向量进行标准化就是将它的长度缩为1.
在OpenGL中,有两个数据类型能够表示一个三维或者四维向量:
- M3DVector3f表示一个三维向量(x,y,z)
- M3DVector4f表示一个四维向量(x,y,z,w)
在典型情况下,w坐标设为1.0。x y z通过除以w来进行缩放。
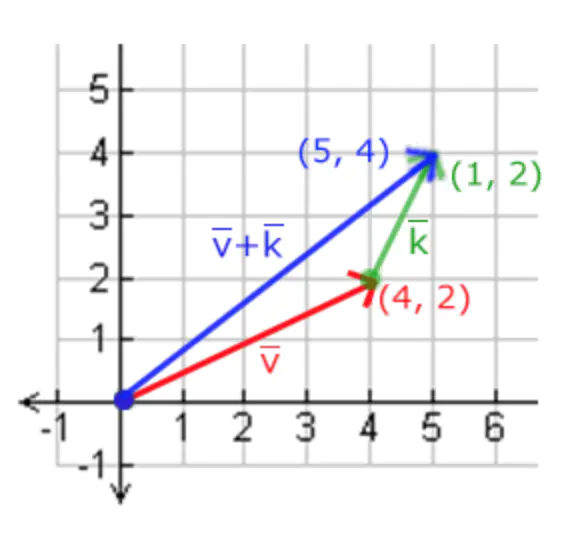
向量也可以进行加减计算。例如:
2.1.1、点乘
在开发中使用的价值非常高的操作就做点乘。 点乘只能发生在两个向量之间进行。两个单元向量进行点乘得到的一个标量,他表示两个向量之间的夹角。
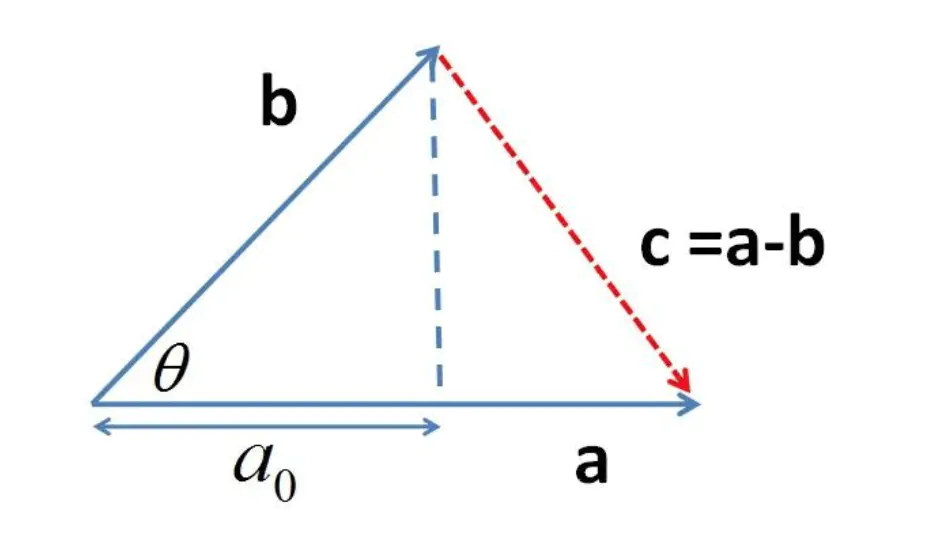
例如: (1,0,0)与(1,1,0)的夹角是45°
运算方式是 1 * 1 + 0 * 1 + 0 * 0 = 1 = cos45°
利用math3d库就是:
- 获取2个向量之间的点乘结果(即
的值)
float m3dDotProduct3(const M3DVector3f u, const M3DVector3f v); - 获取2个向量之间的夹角弧度
float m3dGetAngleBetweenVector3(const M3DVector3f u, const M3DVector3f v);
2.1.2、叉乘
两个向量的叉乘就可以得到另外一个向量,新的向量会与原来的两个向量定义的平面垂直。同事进行叉乘不必为单位向量。
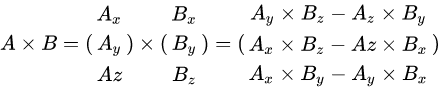
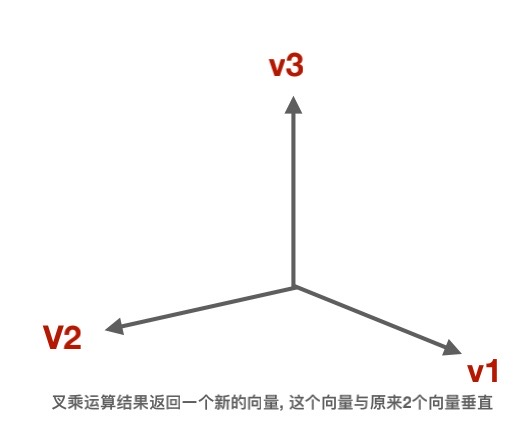
例如V1(1,0,0), V2(0,1,0) 通过计算得到V3(0,0,1)
利用math3d库就是:
void m3dCrossProduct3(M3DVector3f result, const M3DVector3f u, const M3DVector3f v);
2.2、矩阵
矩阵: 矩阵是一个按照长方阵列排列的复数或实数集合。
这就是一个 4 x 4 的矩阵。
在空间中有一个点,使用(x,y,z)来描述他的位置, 此时让其围绕任意位置旋转一定角度后,我们需要知道这个点的新的位置,此时就需要通过矩阵进行计算。
因为新增的位置的x不单纯与原来的x还有旋转的参数有关,甚至于y和z坐标有关。
其他编程标准中,许多矩阵库定义一个矩阵时使用二维数组;OpenGL的约定里,更多倾向使用一维数组;这样做的原因是:OpenGL使用的是Column-Major(以列为主)矩阵排序的约定。

在OpenGL中一个4*4矩阵:
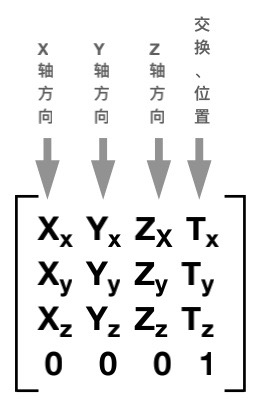
如果将一个对象所有的顶点向量乘以这个矩阵,就能让整个对象变换到空间中给定的位置和方向。
2.2.1、单元矩阵
单元矩阵即对角线为1,其他为0的矩阵:
OpenGL提供的初始化:
void m3dLoadIdentity44f(M3DMatrix44f m);
2.2.2、矩阵的简单计算
矩阵与标量相加:
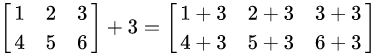
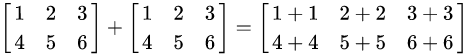
减法与之相同。
矩阵与标量相乘:
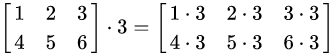
矩阵相乘必须遵守一个法则,左边矩阵的列数与右边矩阵的行数相同时,才能相乘:
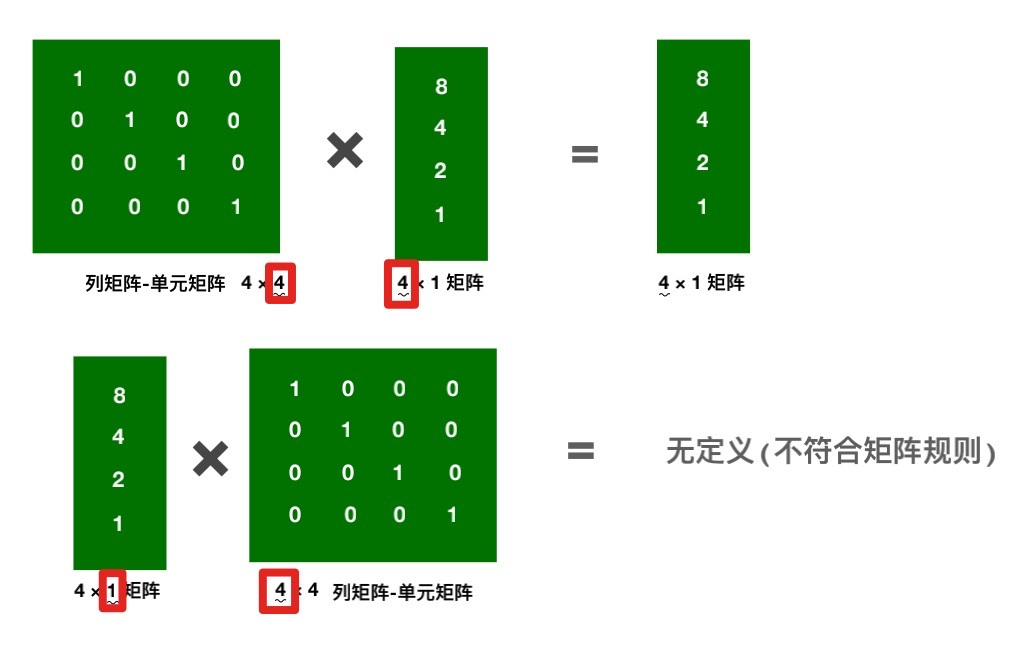
矩阵与单元矩阵相乘,就相当于乘了个1。
矩阵相乘的计算方式为:

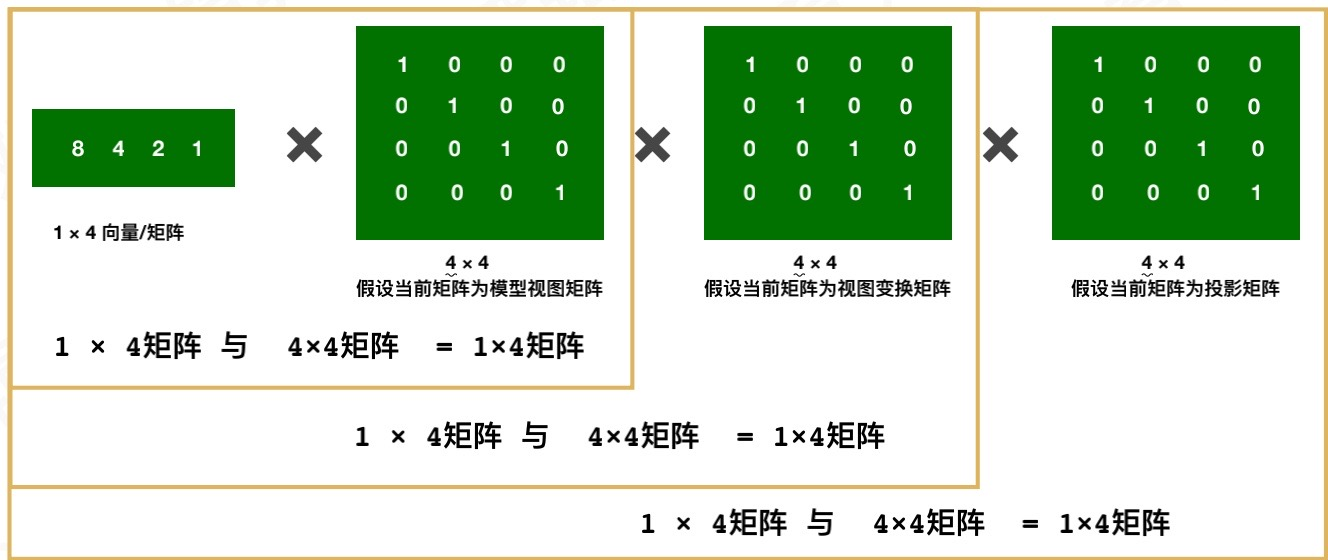
在线性代数数学的维度,为了便于书写。所以坐标计算都是从左往右计算:
变换后的顶点向量 = 顶点(v_local) x 模型矩阵(M_model) x 观察矩阵(M_view) x 投影矩阵(M_pro)
这是经常提到过的MVP
三、OpenGL中的变化
在OpenGL中,有几种变换:
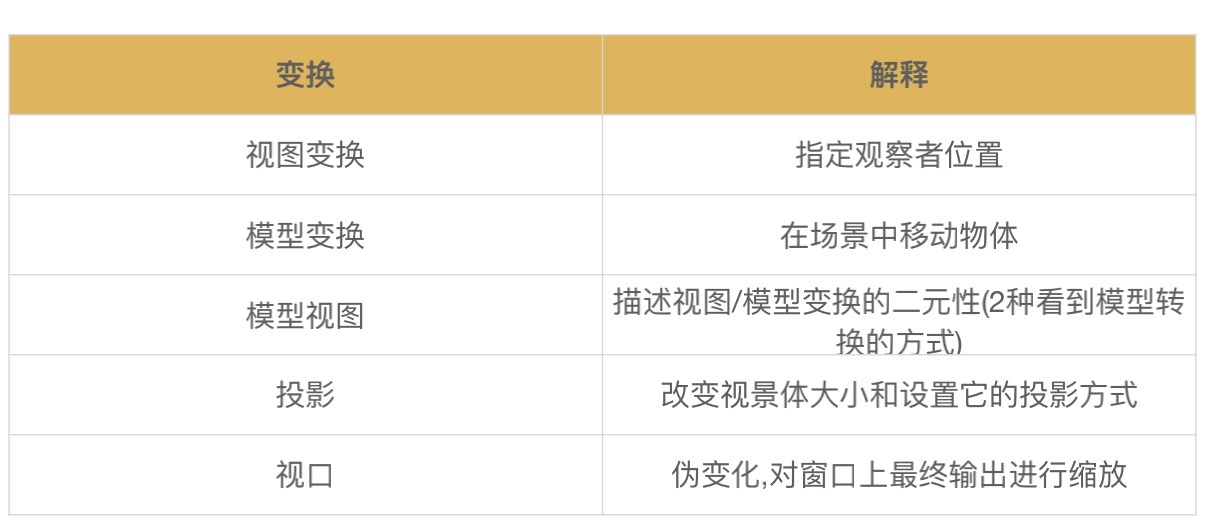
3.1、视图变换
在3D笛卡尔坐标系中,观察者的视图如下:
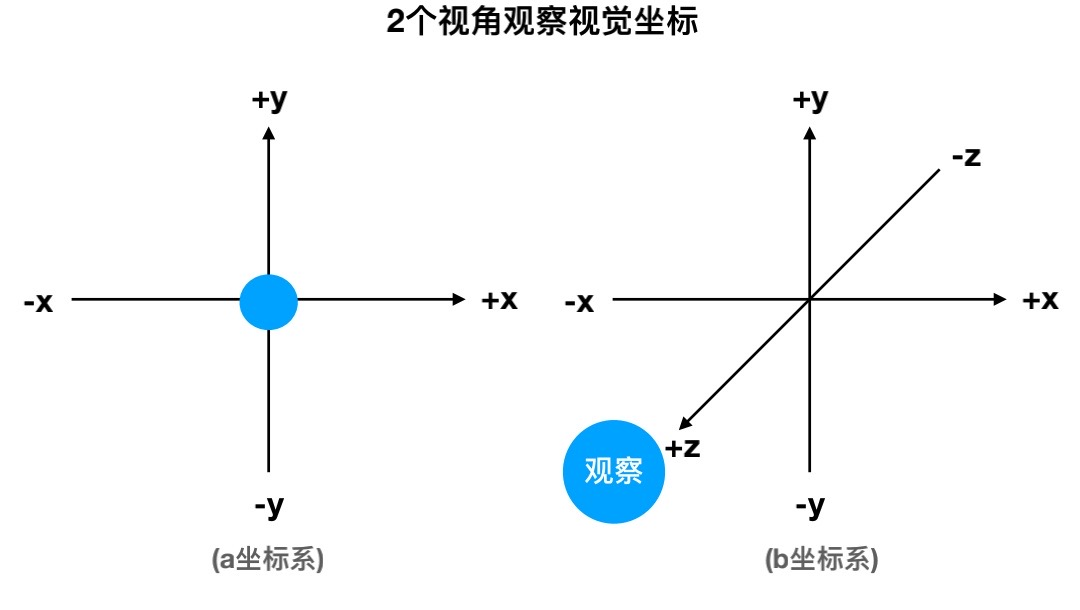
在《OpenGL 超级宝典》这本书中:

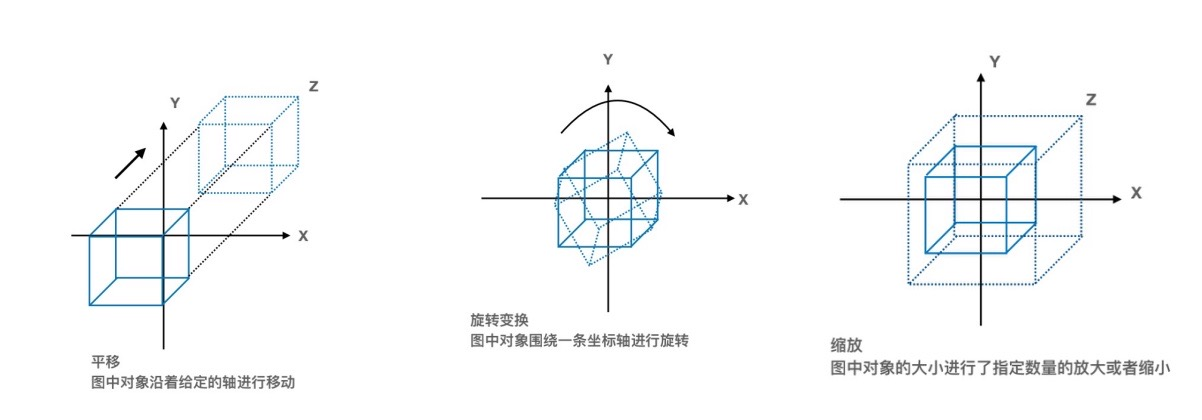
3.2、模型变换
用于操纵模型与其中某特定变换,这些变换将对象移动到需要的位置。通过旋转、缩放、平移。
如果一个模型需要经过多次变化,这些多次变化的变化顺序也会造成不一样的结果(顶点向量不一样):
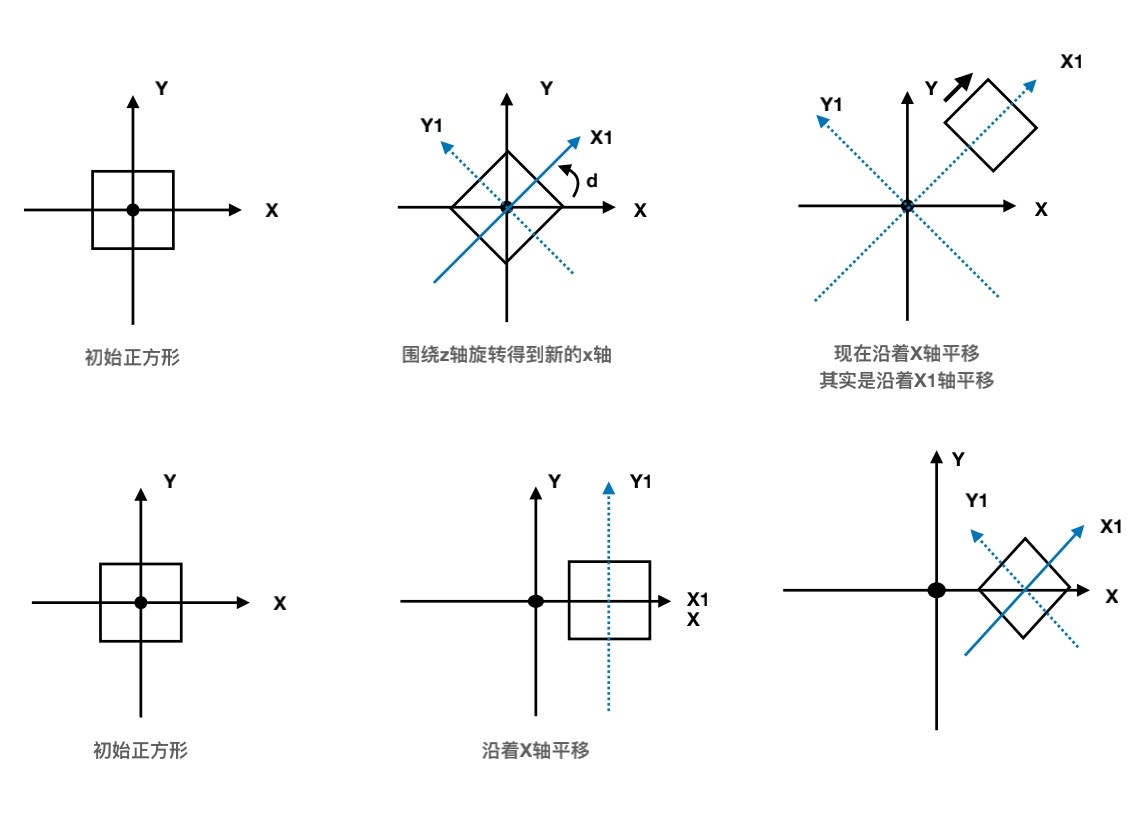
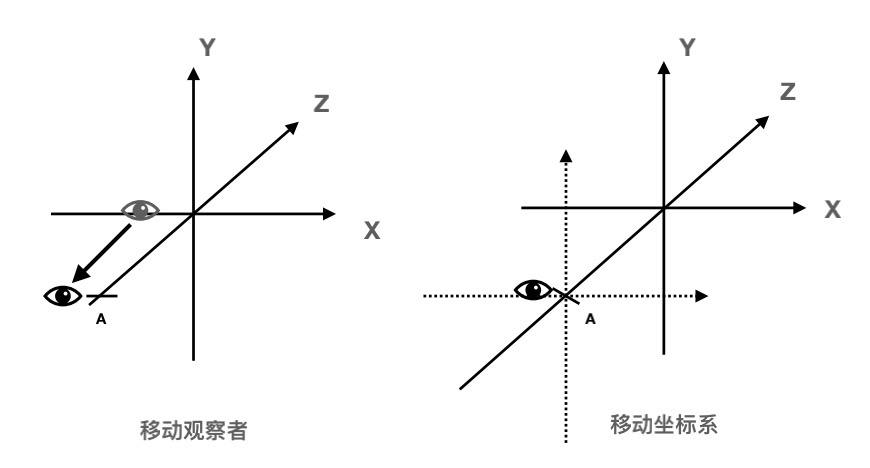
造成物体变换有两种方法:
- 观察者变化
- 物体模型变化
3.3、OpenGL模型变换相关的API
平移: 传入物体模型,分别向 x y z平移多少:
void m3dTranslationMatrix44(M3DMatrix44f m, float x, float y, float z)
旋转: 传入弧度,分别向 x y z旋转多少度:
(这里使用度数转弧度)
m3dRotationMatrix44(m3dDegToRad(45.0), float x, float y, float z)
缩放: 传入物体模型,分别向 x y z缩放多少:
m3dScaleMatrix44(M3DMatrix44f m, float xScale, float yScale, float zScale)
综合变换: 经过多次变化,先执行a变换,再执行b变换
m3dMatrixMultiply44(M3DMatrix44f product, const M3DMatrix44f a, const M3DMatrix44f b);
四、附
在苹果核心动画的官方文档中,也讲解了一些物体模型矩阵变化,它是核心动画最基本的实现原理。