简介
红黑树其实是AVL(自平衡二叉查找树,命名来自于其发明者Adelson-Velskii和Landis),它有如下性质:
- 每个节点的颜色是红色或者黑色
- 根节点是黑色的
- 如果一个节点是红色的,那么它的子节点必须是黑色的
- 从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点
操作说明
- 左旋:让节点变成自己右孩子的左孩子的过程
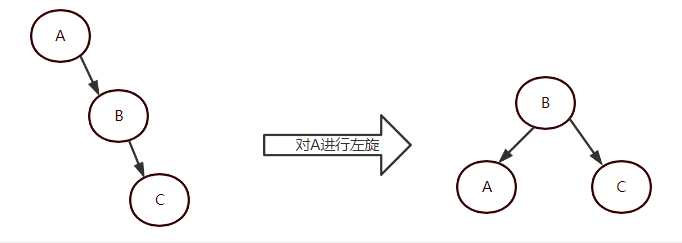
- 右旋:让节点变成自己左孩子的右孩子的过程
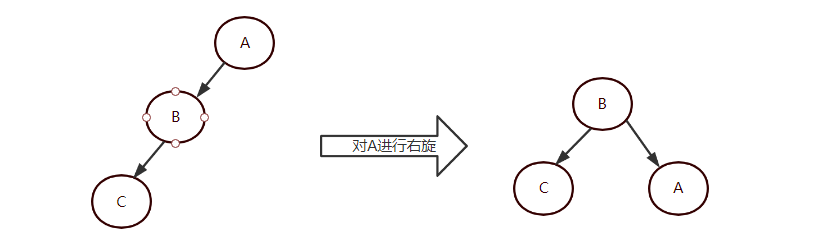
插入
在插入一个新的元素的时候,它的颜色必须是红色,如果是黑色的话,它就会违反条件4。在插入新节点的时候,如果它的父节点是黑色的,则插入完成;如果父节点是红色,就违反了条件3,则需要通过颜色的改变和树的旋转来调整使得整个树满足这4个条件。
我们约定X是新插入的节点,P是它的父节点,U是它的叔叔节点(父节点的兄弟节点),G是祖父节点(父节点的父节点),当U为null的时候,它的颜色为黑色。接下来我们分情况讨论:
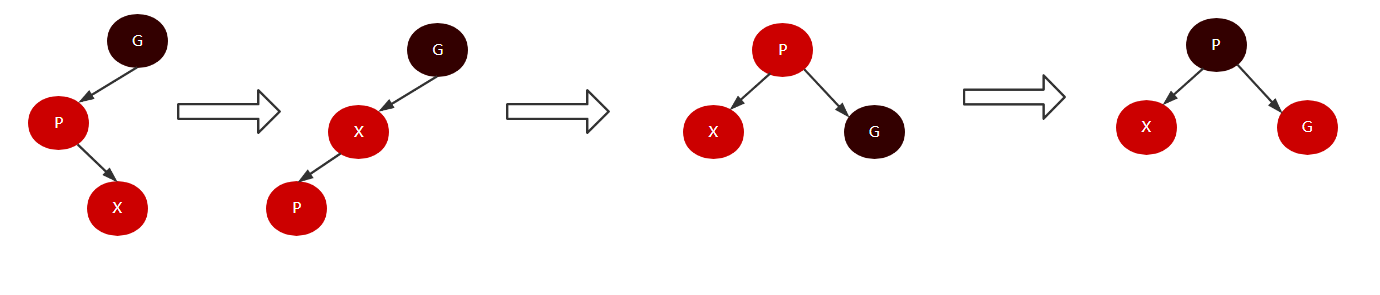
- 当U为黑色(或者为null),此时X、P是红色,G是黑色,X是左儿子。此时我们需要在P和G之间进行单旋转(即对G节点进行右旋),并将新的树的根节点的设置为黑色,这样做是为了防止原来的曾祖节点是红色,过程如下:
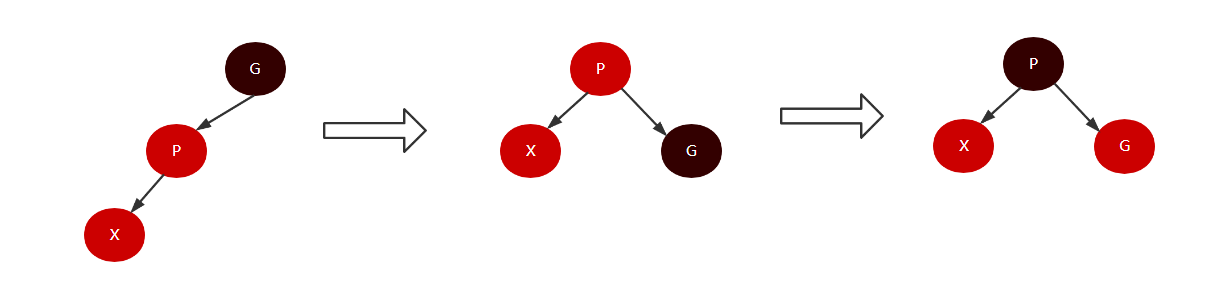
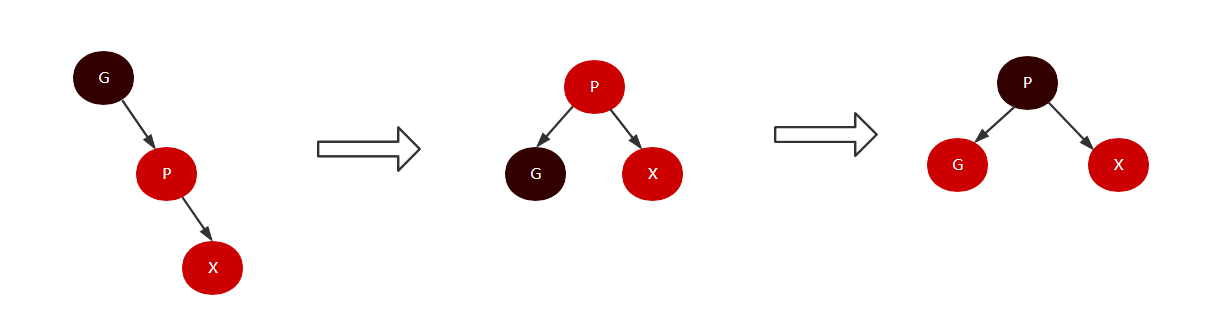
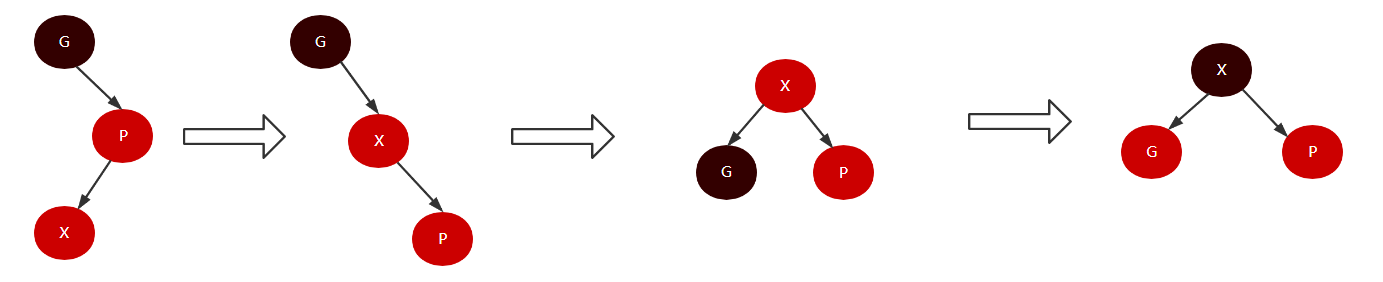
- 当U为黑色(或者为null),此时X、P是红色,G是黑色,X是右儿子。此时需要两次旋转来调整树结构,首先对P进行左旋,此时会变成情况1,再对G进行右旋,过程如下:
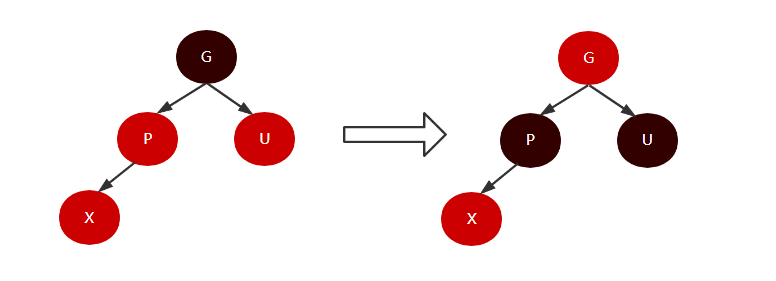
- 当U节点是红色的情况,此时只需要将U、P节点设置为黑色,并将G节点设置为红色,因为将U和P设置为黑色后,违反了条件4,此时需要将G设置为红色来修正;如果G刚好是根节点,此时违反了条件2,需要将G设置为黑色来修正。过程如下:
删除
其实红黑树的删除最终都可以转变成对叶子节点(没有子节点)的删除,我们可以从以下几个情况来讨论:
- 如果需要被删除节点有两个子节点,根据二叉搜索树的性质,我们需要找到它的后继节点(左子树中最大的节点或者右子树中最小的节点),用后继节点的值替换被删除节点的值,然后删除后继节点,如果后继节点有孩子的话,它只能有一个孩子(BST树的性质),此时变成情况2。
- 如果被删除节点只有一个孩子,根据红黑树的性质,此时只存在一种可能,被删除节点是黑色,它的孩子节点是红色且没有孩子节点,我们可以用子节点的值替换被删除节点的值,然后删除子节点。
- 被删除节点本来就是叶子节点。
接下来我们讨论需要修复的情况,只要当实际要被删除的节点是黑色的时候,会破坏性质4,此时我们才需要对树进行修复,此时我们可以分成4种情况(不包含镜像)来进行讨论,我们约定被删除节点为X,其父节点为P,兄弟节点为B,兄弟节点的左孩子为BL,右孩子为BR:
- 如果B是红色(毫无疑问P、BL、BR肯定是黑色),我们将P染成红色,将B染成黑色,并对P进行左旋使其满足情况2,过程如下:

- 如果B是黑色且BL/BR都是黑色(或者都为null),此时我们只需要通过变换颜色就可以重新平衡,将B的颜色改为红色,P的颜色改为黑色,过程如下(因为X是会被删除的,所以此时树已经被修复了):

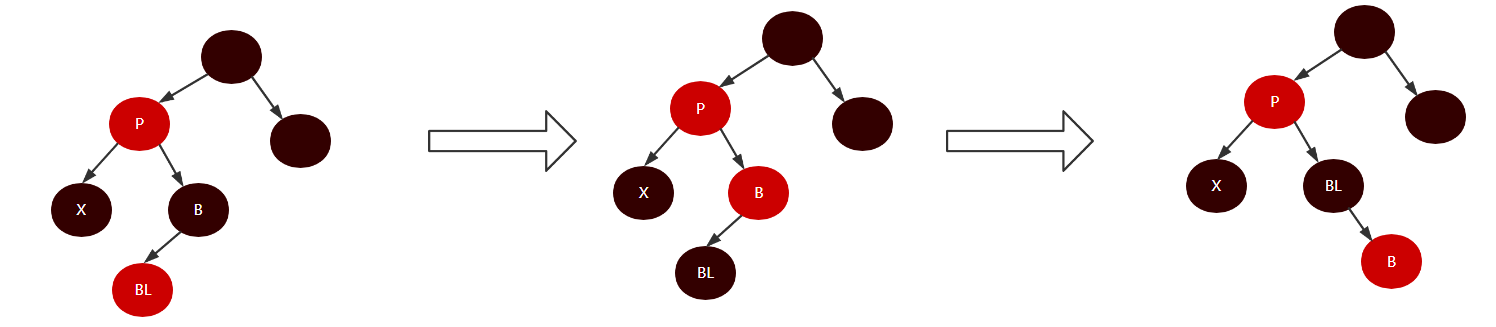
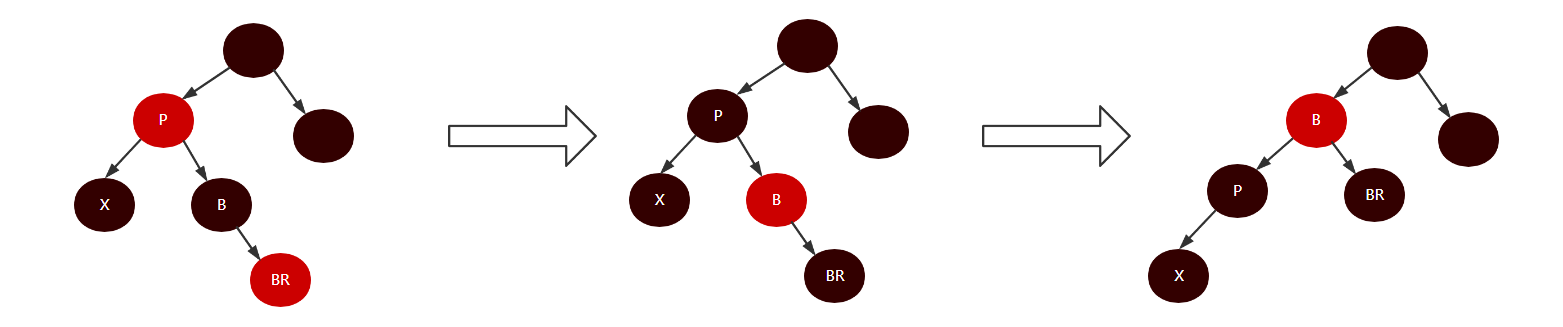
- 如果B是黑色且BL是红色,我们可以将B染成红色,将BL染成黑色,并对B进行右旋转,使其满足情况4,过程如下:
- 如果B是黑色且BR是红色,我们可以将P和BR染成黑色,B染成红色,并对P进行左旋转以达到平衡,过程如下:
实现
采用Java实现,代码中会有对应的注释,所以不再对代码进行单独分析。
/**
* @author rookie-tx
*/
public class RedBlackTree<E extends Comparable<E>> {
private static final boolean RED = true;
private static final boolean BLACK = false;
private TreeNode<E> root;
public RedBlackTree() {
}
public boolean contains(E element) {
TreeNode<E> temp = root;
while (temp != null) {
int compareResult = temp.element.compareTo(element);
if (compareResult > 0) {
temp = temp.left;
} else if (compareResult < 0) {
temp = temp.right;
} else {
return true;
}
}
return false;
}
/**
* 左旋转
* */
private void rotateLeft(TreeNode<E> node) {
if (node == null) {
return;
}
// 将右子树的左子树作为当前节点的右子树
TreeNode<E> r = node.right;
node.right = r.left;
if (r.left != null) {
r.left.parent = node;
}
// 右子树的左子树变成当前节点
TreeNode<E> p = node.parent;
r.left = node;
node.parent = r;
r.parent = p;
if (p == null) {
root = r;
} else if (node == p.left) {
p.left = r;
} else {
p.right = r;
}
}
/**
* 右旋转
* */
private void rotateRight(TreeNode<E> node) {
if (node == null) {
return;
}
TreeNode<E> l = node.left;
node.left = l.right;
if (l.right != null) {
l.right.parent = node;
}
TreeNode<E> p = node.parent;
l.right = node;
l.parent = p;
node.parent = l;
if (p == null) {
root = l;
} else if (p.left == node){
p.left = l;
} else {
p.right = l;
}
}
public boolean add(E element) {
if (element == null) {
throw new NullPointerException();
}
TreeNode<E> newNode = new TreeNode<>(element, RED);
return add(newNode);
}
private boolean add(TreeNode<E> newNode) {
if (root == null) {
root = newNode;
root.color = BLACK;
} else {
TreeNode<E> parent = root;
while (true) {
int compareResult = newNode.element.compareTo(parent.element);
if (compareResult > 0) {
if (parent.right != null) {
parent = parent.right;
} else {
parent.right = newNode;
break;
}
} else if (compareResult < 0) {
if (parent.left != null) {
parent = parent.left;
} else {
parent.left = newNode;
break;
}
} else {
return false;
}
}
newNode.parent = parent;
// 如果父节点是红色,则需要进行平衡
if (parent.color == RED) {
balanceInsertion(newNode);
}
}
return true;
}
/**
* 修复插入,只有父节点是红色的时候才需要重新平衡
* case 1、叔叔节点也为红色
* case 2、是父节点的左孩子,叔叔节点为黑色或没有叔叔节点
* case 3、是父节点的右孩子,叔叔节点为黑色或没有叔叔节点
* */
private void balanceInsertion(TreeNode<E> x) {
//newNode的父节点,爷爷节点,叔叔节点
TreeNode<E> p, g, u;
while (x != null && x != root && x.parent.color == RED) {
p = x.parent; g = p.parent;
if (g != null && p == g.left) {
u = g.right;
if (u == null || u.color == BLACK) {
// CASE 3
if (x == p.right) {
x = p;
rotateLeft(x);
p = x.parent;
}
//CASE 2
p.color = BLACK;
g.color = RED;
rotateRight(g);
} else {
// CASE 1
u.color = BLACK;
p.color = BLACK;
g.color = RED;
x = g;
}
}
// 镜像
else if (g != null && p == g.right) {
u = g.left;
if (u == null || u.color == BLACK) {
// CASE 3
if (x == p.left) {
x = p;
rotateRight(x);
p = x.parent;
}
// CASE 2
p.color = BLACK;
g.color = RED;
rotateLeft(g);
} else {
// CASE 1
u.color = BLACK;
p.color = BLACK;
g.color = RED;
x = g;
}
}
}
// CASE 1的情况,需要将root染红
root.color = BLACK;
}
public boolean delete(E element) {
TreeNode<E> currentNode = root;
while (currentNode != null) {
int compareResult = currentNode.element.compareTo(element);
if (compareResult > 0) {
currentNode = currentNode.left;
} else if (compareResult < 0) {
currentNode = currentNode.right;
} else {
if (currentNode.left != null && currentNode.right != null) {
TreeNode<E> successor = currentNode.right;
while (successor.left != null) {
successor = successor.left;
}
currentNode.element = successor.element;
currentNode = successor;
}
if (currentNode.left != null) {
currentNode.element = currentNode.left.element;
currentNode = currentNode.left;
} else if (currentNode.right != null) {
currentNode.element = currentNode.right.element;
currentNode = currentNode.right;
}
// 只有根节点的情况
if (currentNode.parent == null) {
root = null;
return true;
}
if (currentNode.color == BLACK) {
balanceDeletion(currentNode);
}
if (currentNode == currentNode.parent.left) {
currentNode.parent.left = null;
} else {
currentNode.parent.right = null;
}
currentNode.parent = null;
return true;
}
}
return true;
}
/**
* 修复删除
* case 1、兄弟节点是红色
* case 2、兄弟节点是黑色,兄弟节点的孩子节点也是黑色
* case 3、兄弟节点是黑色,兄弟节点的左孩子是红色,右孩子是黑色
* case 4、兄弟节点是黑色,兄弟节点的右孩子是红色,左孩子是任意色
* */
private void balanceDeletion(TreeNode<E> x) {
TreeNode<E> p, b;
while (x != root && x.color == BLACK) {
p = x.parent;
if (x == p.left) {
b = p.right;
// CASE 1
if (b != null && b.color == RED) {
b.color = BLACK;
p.color = RED;
rotateLeft(p);
b = p.right;
}
// CASE 2
if (b != null && (b.left == null || b.left.color == BLACK) &&
(b.right == null || b.right.color == BLACK)) {
b.color = RED;
x = p;
} else {
// CASE 3
if (b != null && b.left != null && b.left.color == RED) {
b.color = RED;
b.left.color = BLACK;
rotateRight(b);
b = p.right;
}
// CASE 4
p.color = BLACK;
if (b != null) {
b.color = RED;
if (b.right != null) {
b.right.color = BLACK;
}
}
rotateLeft(p);
x = root;
}
} else {
b = p.left;
// CASE 1
if (b != null && b.color == RED) {
b.color = BLACK;
p.color = RED;
rotateRight(p);
b = p.left;
}
// CASE 2
if (b != null && (b.left == null || b.left.color == BLACK) &&
(b.right == null || b.right.color == BLACK)) {
b.color = RED;
x = p;
} else {
// CASE 3
if (b != null && b.right != null && b.right.color == RED) {
b.color = RED;
b.right.color = BLACK;
rotateLeft(b);
b = p.left;
}
// CASE 4
p.color = BLACK;
if (b != null) {
b.color = RED;
if (b.left != null) {
b.left.color = BLACK;
}
}
rotateRight(p);
x = root;
}
}
}
if (x != null) {
x.color = BLACK;
}
}
static class TreeNode<E extends Comparable<E>> {
E element;
TreeNode<E> left;
TreeNode<E> right;
TreeNode<E> parent;
boolean color;
TreeNode(E element, boolean color) {
this.element = element;
this.color = color;
}
}
}
代码写的比较粗糙。。。推荐大家可以看看JDK中TreeMap的实现。